1.5 三角函数的应用同步练习 2023-2024学年北师大版九年级数学下册(含答案)
文档属性
| 名称 | 1.5 三角函数的应用同步练习 2023-2024学年北师大版九年级数学下册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 385.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 12:36:10 | ||
图片预览

文档简介
1.5 三角函数的应用同步练习2023-2024学年北师大版九年级数学下册
一、单选题(共10题;共30分)
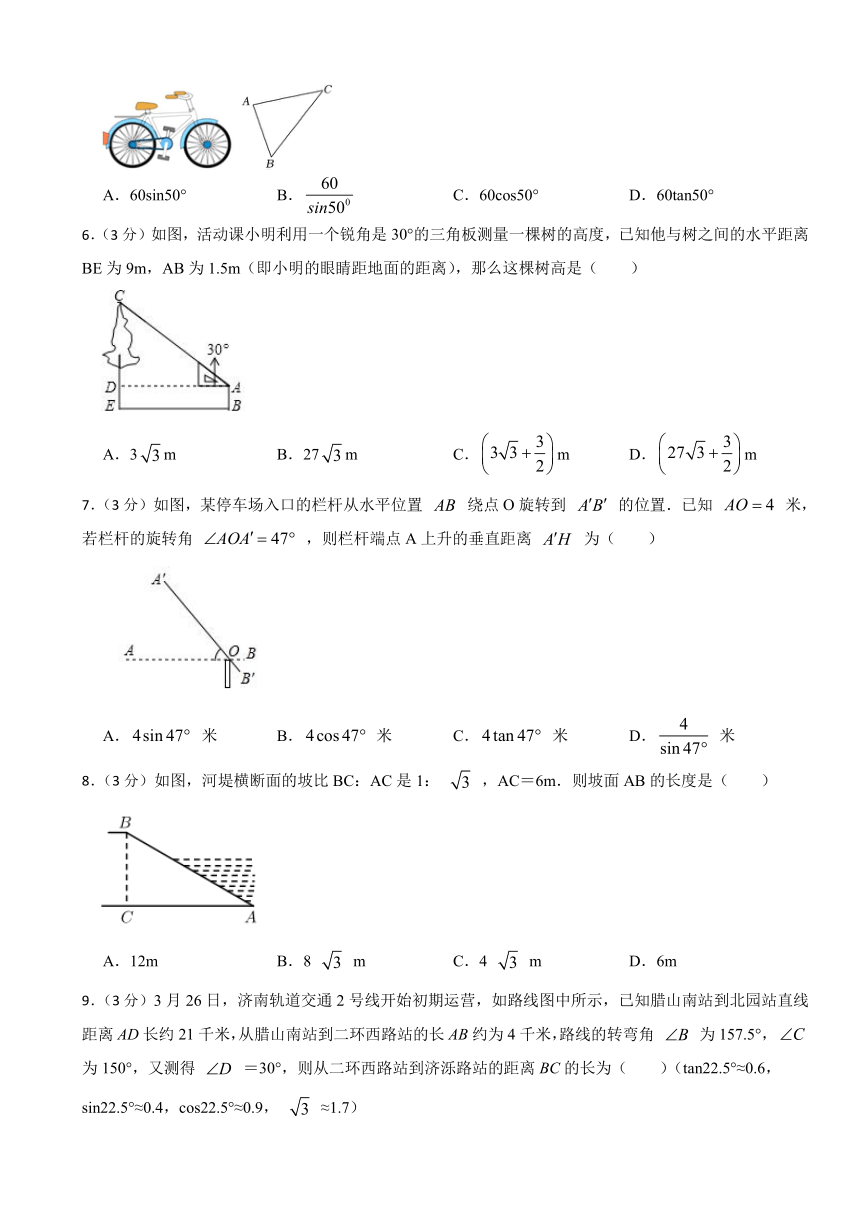
1.(3分)如图,在天定山滑雪场滑雪,需从山脚下处乘缆车上山顶处,缆车索道与水平线所成的,若山的高度米,则缆车索道的长为( )
A.米 B.米 C.米 D.米
2.(3分)如图,拦水坝的横断面是梯形,高 米,斜面坡度为 ,则斜坡 的长为( )
A. 米 B. 米 C. 米 D. 米
3.(3分)如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为 ,则高BC是( )
A. 米 B. 米 C. 米 D. 米
4.(3分)如图,要得到从点D观测点A的俯角,可以测量( )
A.∠ADC B.∠DCE C.∠ADB D.∠DAB
5.(3分)如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得∠A=88°,∠C=42°,AB=60,则点A到BC的距离为( )
A.60sin50° B. C.60cos50° D.60tan50°
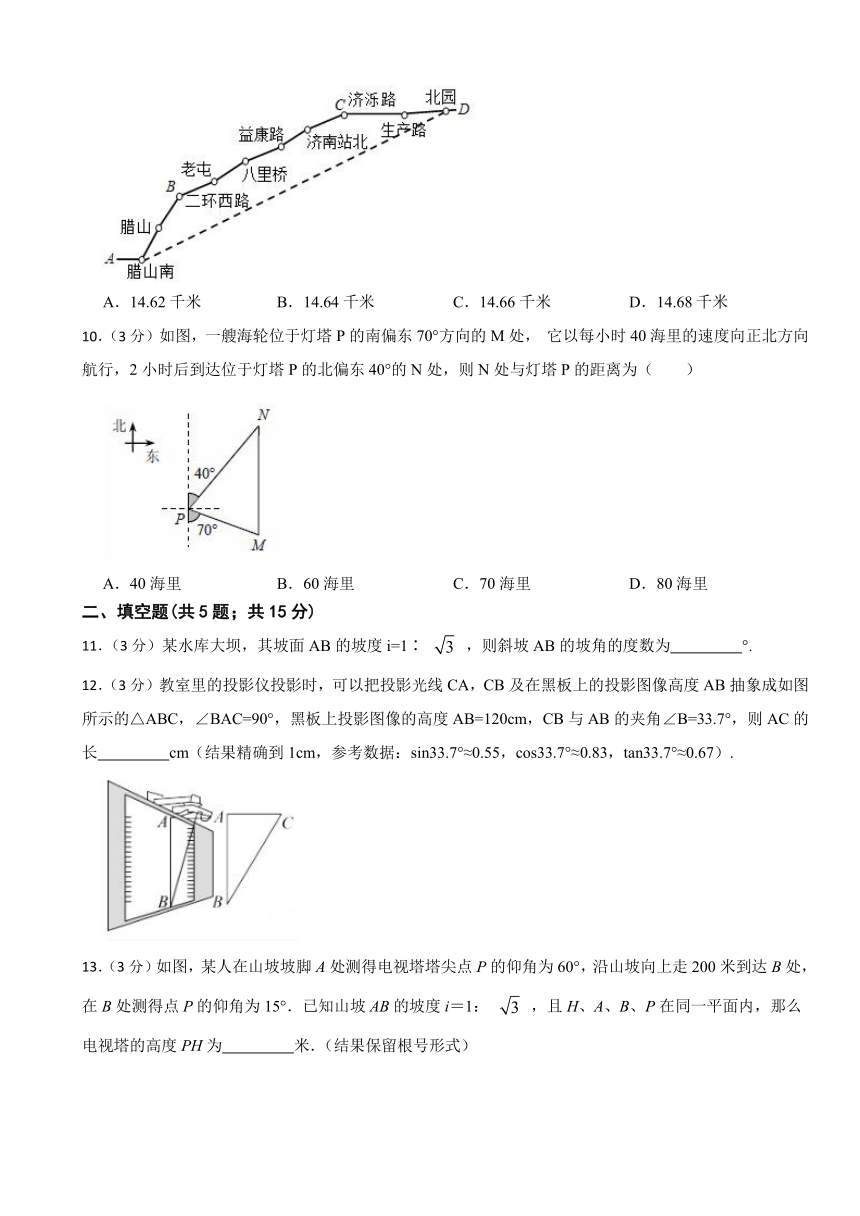
6.(3分)如图,活动课小明利用一个锐角是30°的三角板测量一棵树的高度,已知他与树之间的水平距离BE为9m,AB为1.5m(即小明的眼睛距地面的距离),那么这棵树高是( )
A.3m B.27m C.m D.m
7.(3分)如图,某停车场入口的栏杆从水平位置 绕点O旋转到 的位置.已知 米,若栏杆的旋转角 ,则栏杆端点A上升的垂直距离 为( )
A. 米 B. 米 C. 米 D. 米
8.(3分)如图,河堤横断面的坡比BC:AC是1: ,AC=6m.则坡面AB的长度是( )
A.12m B.8 m C.4 m D.6m
9.(3分)3月26日,济南轨道交通2号线开始初期运营,如路线图中所示,已知腊山南站到北园站直线距离AD长约21千米,从腊山南站到二环西路站的长AB约为4千米,路线的转弯角 为157.5°, 为150°,又测得 =30°,则从二环西路站到济泺路站的距离BC的长为( )(tan22.5°≈0.6,sin22.5°≈0.4,cos22.5°≈0.9, ≈1.7)
A.14.62千米 B.14.64千米 C.14.66千米 D.14.68千米
10.(3分)如图,一艘海轮位于灯塔P的南偏东70°方向的M处, 它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( )
A.40海里 B.60海里 C.70海里 D.80海里
二、填空题(共5题;共15分)
11.(3分)某水库大坝,其坡面AB的坡度i=1∶ ,则斜坡AB的坡角的度数为 °.
12.(3分)教室里的投影仪投影时,可以把投影光线CA,CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC,∠BAC=90°,黑板上投影图像的高度AB=120cm,CB与AB的夹角∠B=33.7°,则AC的长 cm(结果精确到1cm,参考数据:sin33.7°≈0.55,cos33.7°≈0.83,tan33.7°≈0.67).
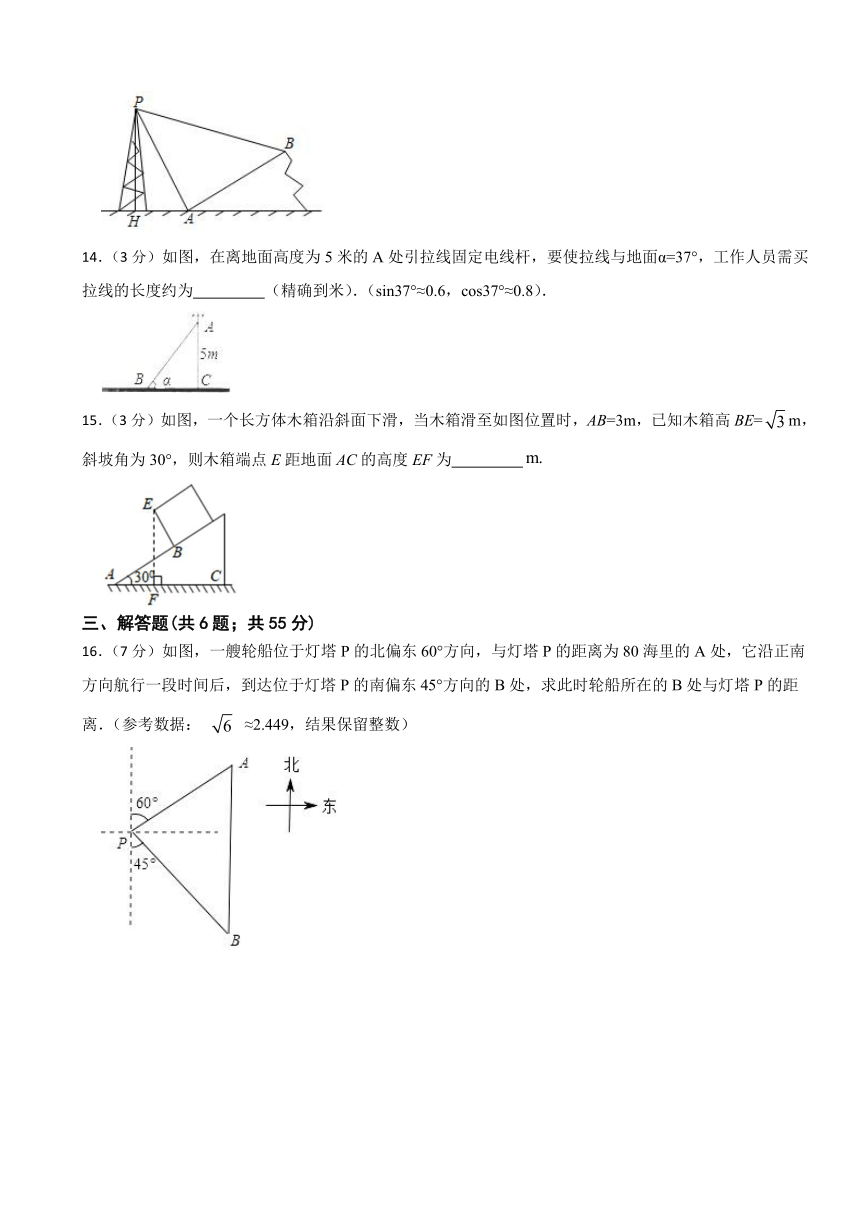
13.(3分)如图,某人在山坡坡脚A处测得电视塔塔尖点P的仰角为60°,沿山坡向上走200米到达B处,在B处测得点P的仰角为15°.已知山坡AB的坡度i=1: ,且H、A、B、P在同一平面内,那么电视塔的高度PH为 米.(结果保留根号形式)
14.(3分)如图,在离地面高度为5米的A处引拉线固定电线杆,要使拉线与地面α=37°,工作人员需买拉线的长度约为 (精确到米).(sin37°≈0.6,cos37°≈0.8).
15.(3分)如图,一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE=m,斜坡角为30°,则木箱端点E距地面AC的高度EF为
三、解答题(共6题;共55分)
16.(7分)如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据: ≈2.449,结果保留整数)
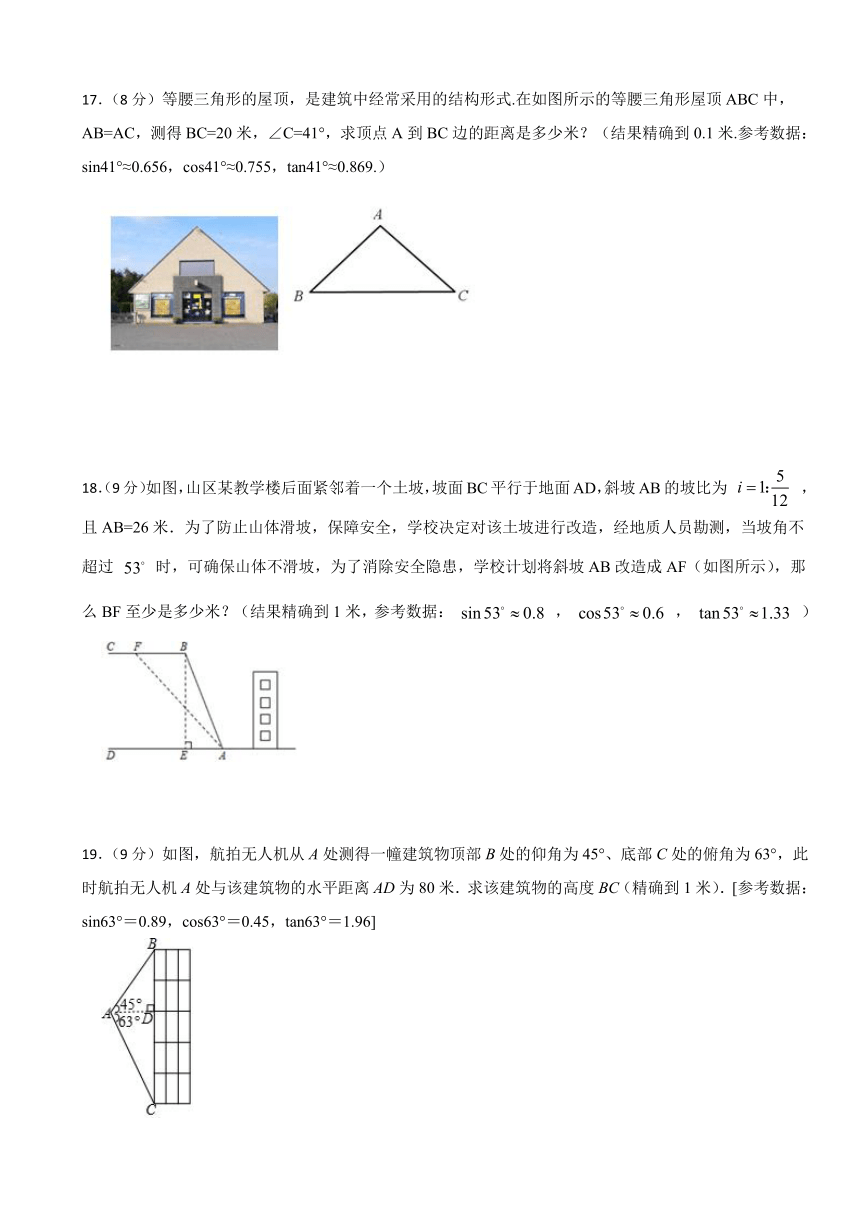
17.(8分)等腰三角形的屋顶,是建筑中经常采用的结构形式.在如图所示的等腰三角形屋顶ABC中,AB=AC,测得BC=20米,∠C=41°,求顶点A到BC边的距离是多少米?(结果精确到0.1米.参考数据:sin41°≈0.656,cos41°≈0.755,tan41°≈0.869.)
18.(9分)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为 ,且AB=26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过 时,可确保山体不滑坡,为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米,参考数据: , , )
19.(9分)如图,航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为63°,此时航拍无人机A处与该建筑物的水平距离AD为80米.求该建筑物的高度BC(精确到1米).[参考数据:sin63°=0.89,cos63°=0.45,tan63°=1.96]
20.(10分)为维护我国海洋权益,强化管辖海域的实际控制,国家海洋局决定实施常态化的海洋维权巡航执法,开展多种形式的海洋维权行动:外国船只除特许外,不得进入我国海洋100海里以内的区域。如图,设A、B是我们的观察站,A和B之间的距离为160海里,海岸线是过A、B的一条直线。一外国船只在C点,在A点测得∠BAC=45°,同时在B点测得∠ABC=60°,问此时是否要向外国船只发出警告,令其退出我国海域。
21.(12分)如图,已知在中,点D是边上一点,且,点E是边上一点,且.
(1)(6分)求证:;
(2)(6分)若,,,求的值.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】D
5.【答案】A
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】30
12.【答案】80
13.【答案】100
14.【答案】8
15.【答案】3
16.【答案】解:作PC⊥AB交于C点,由题意可得∠APC=30°,∠BPC=45°,AP=80(海里).在Rt△APC中,PC=PA cos∠APC=40 (海里).在Rt△PCB中,PB= ≈98(海里).答:此时轮船所在的B处与灯塔P的距离是98海里.
17.【答案】解:作AD丄BC,垂足为D点
∵AB=AC,BC=20,
∴BD=CD= BC=10.
在Rt△ACD中,∠C=41°,
∴tan C=tan41°= ,
∴AD= ≈10×0.869 ≈8.7.
答:顶点A到BC边的距离是8.7米.
18.【答案】解:过点F作FH⊥AD于H,
则四边形FHEB为矩形,
∴FH=BE,BF=HE,
∵斜坡AB的坡比为 ,
∴BE:AE=12:5,
设BE=12x米,则AE=5x米,
在Rt△ABE中,AB2=AE2+BE2,即262=(12x)2+(5x)2,
解得:x1=2,x2= 2(舍去),
则AE=10米,BE=FH=24米,
在Rt△FAH中,tan∠FAH= ,
∴AH= ≈ (米),
∴BF=HE=AH AE=18 10=8(米),
答:BF至少是8米.
19.【答案】解:在△ADB中,∠ADB=90°,∠BAD=45°,
∴BD=AD=80(米),
在△ACD中,∠ADC=90°,
∴CD=AD tan63°=80×1.96≈156.8(米),
∴BC=BD+CD=80+156.8=236.8≈237(米),
答:该建筑物的高度BC约为237米.
20.【答案】解:过点C做CD⊥AB于D
则△ACD、△ABD为直角三角形°
∠A=45°
∠ACD=90°-45°=45°
AD=CD
设AD=x则CD=x BD=160-x
又∠B=60°
tan600=
=
解得
检验:当 时 160-x≠0
所以 是原方程的解
>100
所以不需要向外国船只提出警告
21.【答案】(1)证明:,
,
,
,
;
(2)解:过点作于点,
,
,
,
则,
,
在中,,
解得:,
,
.
一、单选题(共10题;共30分)
1.(3分)如图,在天定山滑雪场滑雪,需从山脚下处乘缆车上山顶处,缆车索道与水平线所成的,若山的高度米,则缆车索道的长为( )
A.米 B.米 C.米 D.米
2.(3分)如图,拦水坝的横断面是梯形,高 米,斜面坡度为 ,则斜坡 的长为( )
A. 米 B. 米 C. 米 D. 米
3.(3分)如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为 ,则高BC是( )
A. 米 B. 米 C. 米 D. 米
4.(3分)如图,要得到从点D观测点A的俯角,可以测量( )
A.∠ADC B.∠DCE C.∠ADB D.∠DAB
5.(3分)如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得∠A=88°,∠C=42°,AB=60,则点A到BC的距离为( )
A.60sin50° B. C.60cos50° D.60tan50°
6.(3分)如图,活动课小明利用一个锐角是30°的三角板测量一棵树的高度,已知他与树之间的水平距离BE为9m,AB为1.5m(即小明的眼睛距地面的距离),那么这棵树高是( )
A.3m B.27m C.m D.m
7.(3分)如图,某停车场入口的栏杆从水平位置 绕点O旋转到 的位置.已知 米,若栏杆的旋转角 ,则栏杆端点A上升的垂直距离 为( )
A. 米 B. 米 C. 米 D. 米
8.(3分)如图,河堤横断面的坡比BC:AC是1: ,AC=6m.则坡面AB的长度是( )
A.12m B.8 m C.4 m D.6m
9.(3分)3月26日,济南轨道交通2号线开始初期运营,如路线图中所示,已知腊山南站到北园站直线距离AD长约21千米,从腊山南站到二环西路站的长AB约为4千米,路线的转弯角 为157.5°, 为150°,又测得 =30°,则从二环西路站到济泺路站的距离BC的长为( )(tan22.5°≈0.6,sin22.5°≈0.4,cos22.5°≈0.9, ≈1.7)
A.14.62千米 B.14.64千米 C.14.66千米 D.14.68千米
10.(3分)如图,一艘海轮位于灯塔P的南偏东70°方向的M处, 它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( )
A.40海里 B.60海里 C.70海里 D.80海里
二、填空题(共5题;共15分)
11.(3分)某水库大坝,其坡面AB的坡度i=1∶ ,则斜坡AB的坡角的度数为 °.
12.(3分)教室里的投影仪投影时,可以把投影光线CA,CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC,∠BAC=90°,黑板上投影图像的高度AB=120cm,CB与AB的夹角∠B=33.7°,则AC的长 cm(结果精确到1cm,参考数据:sin33.7°≈0.55,cos33.7°≈0.83,tan33.7°≈0.67).
13.(3分)如图,某人在山坡坡脚A处测得电视塔塔尖点P的仰角为60°,沿山坡向上走200米到达B处,在B处测得点P的仰角为15°.已知山坡AB的坡度i=1: ,且H、A、B、P在同一平面内,那么电视塔的高度PH为 米.(结果保留根号形式)
14.(3分)如图,在离地面高度为5米的A处引拉线固定电线杆,要使拉线与地面α=37°,工作人员需买拉线的长度约为 (精确到米).(sin37°≈0.6,cos37°≈0.8).
15.(3分)如图,一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE=m,斜坡角为30°,则木箱端点E距地面AC的高度EF为
三、解答题(共6题;共55分)
16.(7分)如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据: ≈2.449,结果保留整数)
17.(8分)等腰三角形的屋顶,是建筑中经常采用的结构形式.在如图所示的等腰三角形屋顶ABC中,AB=AC,测得BC=20米,∠C=41°,求顶点A到BC边的距离是多少米?(结果精确到0.1米.参考数据:sin41°≈0.656,cos41°≈0.755,tan41°≈0.869.)
18.(9分)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为 ,且AB=26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过 时,可确保山体不滑坡,为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米,参考数据: , , )
19.(9分)如图,航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为63°,此时航拍无人机A处与该建筑物的水平距离AD为80米.求该建筑物的高度BC(精确到1米).[参考数据:sin63°=0.89,cos63°=0.45,tan63°=1.96]
20.(10分)为维护我国海洋权益,强化管辖海域的实际控制,国家海洋局决定实施常态化的海洋维权巡航执法,开展多种形式的海洋维权行动:外国船只除特许外,不得进入我国海洋100海里以内的区域。如图,设A、B是我们的观察站,A和B之间的距离为160海里,海岸线是过A、B的一条直线。一外国船只在C点,在A点测得∠BAC=45°,同时在B点测得∠ABC=60°,问此时是否要向外国船只发出警告,令其退出我国海域。
21.(12分)如图,已知在中,点D是边上一点,且,点E是边上一点,且.
(1)(6分)求证:;
(2)(6分)若,,,求的值.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】D
5.【答案】A
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】30
12.【答案】80
13.【答案】100
14.【答案】8
15.【答案】3
16.【答案】解:作PC⊥AB交于C点,由题意可得∠APC=30°,∠BPC=45°,AP=80(海里).在Rt△APC中,PC=PA cos∠APC=40 (海里).在Rt△PCB中,PB= ≈98(海里).答:此时轮船所在的B处与灯塔P的距离是98海里.
17.【答案】解:作AD丄BC,垂足为D点
∵AB=AC,BC=20,
∴BD=CD= BC=10.
在Rt△ACD中,∠C=41°,
∴tan C=tan41°= ,
∴AD= ≈10×0.869 ≈8.7.
答:顶点A到BC边的距离是8.7米.
18.【答案】解:过点F作FH⊥AD于H,
则四边形FHEB为矩形,
∴FH=BE,BF=HE,
∵斜坡AB的坡比为 ,
∴BE:AE=12:5,
设BE=12x米,则AE=5x米,
在Rt△ABE中,AB2=AE2+BE2,即262=(12x)2+(5x)2,
解得:x1=2,x2= 2(舍去),
则AE=10米,BE=FH=24米,
在Rt△FAH中,tan∠FAH= ,
∴AH= ≈ (米),
∴BF=HE=AH AE=18 10=8(米),
答:BF至少是8米.
19.【答案】解:在△ADB中,∠ADB=90°,∠BAD=45°,
∴BD=AD=80(米),
在△ACD中,∠ADC=90°,
∴CD=AD tan63°=80×1.96≈156.8(米),
∴BC=BD+CD=80+156.8=236.8≈237(米),
答:该建筑物的高度BC约为237米.
20.【答案】解:过点C做CD⊥AB于D
则△ACD、△ABD为直角三角形°
∠A=45°
∠ACD=90°-45°=45°
AD=CD
设AD=x则CD=x BD=160-x
又∠B=60°
tan600=
=
解得
检验:当 时 160-x≠0
所以 是原方程的解
>100
所以不需要向外国船只提出警告
21.【答案】(1)证明:,
,
,
,
;
(2)解:过点作于点,
,
,
,
则,
,
在中,,
解得:,
,
.
