2023-2024学年数学九年级下册北师大版第一章直角三角形的边角关系(含解析)
文档属性
| 名称 | 2023-2024学年数学九年级下册北师大版第一章直角三角形的边角关系(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学九年级下册北师大版第一章直角三角形的边角关系
一、单选题
1.的相反数是( )
A.1 B. C. D.
2.如图,在中,,,下列用线段比表示的值,错误的是( )
A. B. C. D.
3.如图,在中,,若,,则的值为( )
A. B. C. D.
4.2022年2月4日第24届冬季奥运会在北京举办,某校也开展了丰富多彩的冰雪活动.如图是该校同学参加的冰雪项目学习,小嵩乘滑雪板沿斜坡滑雪道直线滑行,若滑行距离米,斜坡滑雪道与水平面的夹角为,则他下降的高度为( )
A.米 B.米 C.米 D.米
5.下列式子错误的是( )
A. B.
C. D.
6.的边长都扩大2倍,则的值( )
A.不变 B.变大 C.变小 D.无法判断
7.在中,,如果,,那么等于( )
A. B. C. D.
8.如果中,,则下列结论正确的是( )
A.是等边三角形 B.是钝角三角形
C.是等腰直角三角形 D.是锐角三角形
二、填空题
9.计算: .
10.已知锐角满足,则 .
11.已知,锐角的正切值是3,则它的余弦值是 .
12.如图,在中,,于点D,,,那么 .
13.已知为锐角,且,则的值为 .
14.已知一条斜坡的长度为13米,高度为5米,那么该斜坡的坡度为 .
15.如图,小明在点C处测得树的顶端A仰角为,测得米,则树的高(单位:米)为 .
16.河堤横断面如图所示,迎水坡的坡比为,则 .
三、解答题
17.计算:.
18.在中,,,,解这个直角三角形.
19.先化简,再求代数式的值,其中.
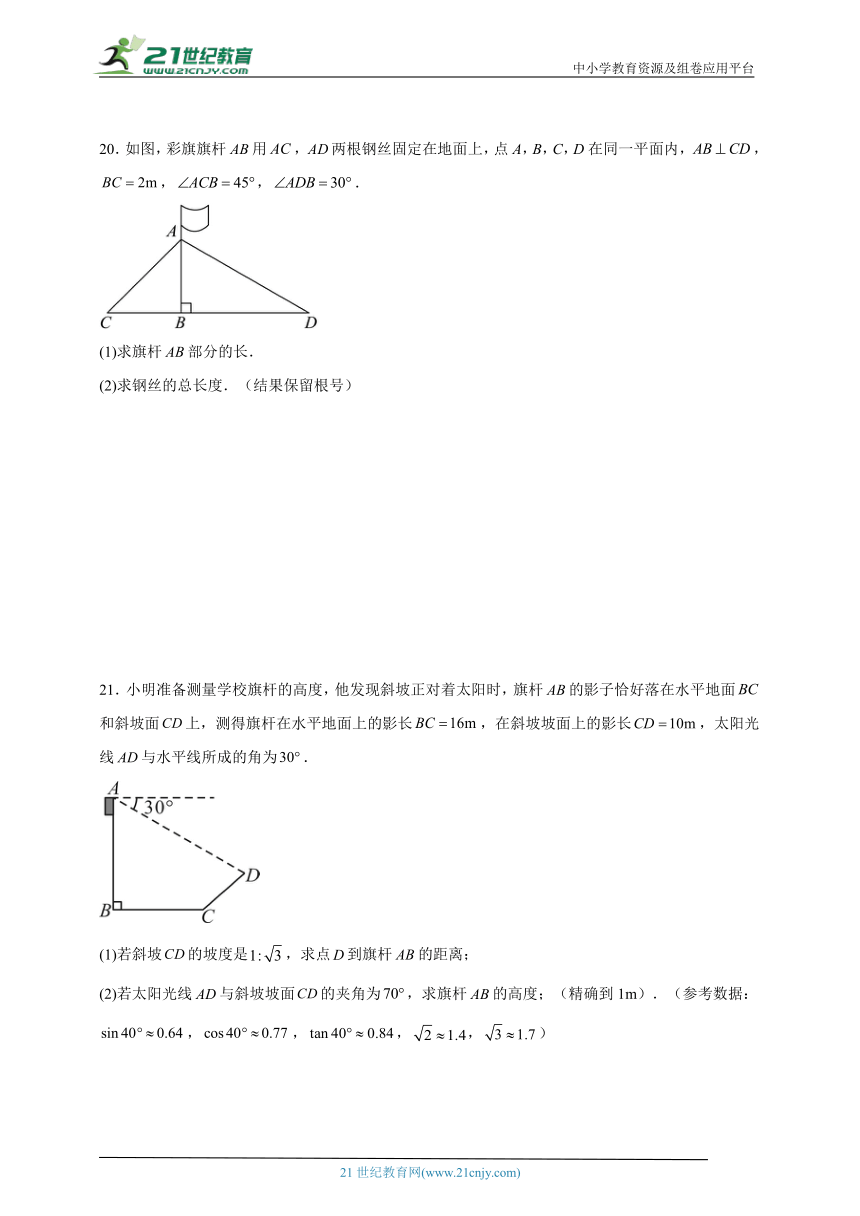
20.如图,彩旗旗杆用,两根钢丝固定在地面上,点A,B,C,D在同一平面内,,,,.
(1)求旗杆部分的长.
(2)求钢丝的总长度.(结果保留根号)
21.小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆的影子恰好落在水平地面和斜坡面上,测得旗杆在水平地面上的影长,在斜坡坡面上的影长,太阳光线与水平线所成的角为.
(1)若斜坡的坡度是,求点到旗杆的距离;
(2)若太阳光线与斜坡坡面的夹角为,求旗杆的高度;(精确到1m).(参考数据:,,,,)
22.如图,在中,点E是中点.点F是中点.连接平分.
(1)求证:四边形是菱形:
(2)连接,与交于点O,连接.若,,求的长.
参考答案:
1.B
【分析】本题考查了相反数的定义,特殊角的三角函数值,掌握特殊角的三角函数值是解题的关键.根据特殊角的三角函数值以及相反数的定义即可求解.
【详解】解:∵,
∴的相反数是.
故选:B.
2.D
【分析】本题考查了锐角三角函数关系,正确把握锐角三角函数定义是解题关键.根据锐角三角函数关系的定义分析得出答案.
【详解】解:∵在中,,,
∴,,
∴,
∴.
∴A,B,C正确,不符合题意,D错误,符合题意,
故选:D.
3.D
【分析】本题考查了锐角三角函数的定义,能熟记锐角三角函数的定义是解此题的关键.根据锐角三角函数的定义得出,再代入求出答案即可.
【详解】解:,,,
∴,
故选:D.
4.B
【分析】本题考查的是解直角三角形的应用坡度坡角问题.过点作水平面于点,根据正弦的定义计算即可.
【详解】解:如图,过点作水平面于点,
在中,,米,
,
(米),
故选:B.
5.C
【分析】本题考查三角函数计算.根据题意熟记特殊角三角函数值是解决本题的关键,逐一计算选项即可选出本题答案.
【详解】解:A、∵,故A选项正确;
B、∵,故B选项正确;
C、∵,
∴,故C选项不正确;
D、∵,故D选项正确;
故选:C.
6.A
【分析】本题考查了解直角三角形,熟练掌握锐角三角函数的定义是解题的关键.根据题意可得所得的三角形与原三角形相似,从而可得的大小没有发生变化,即可解答.
【详解】解:∵的边长都扩大2倍,
∴所得的三角形与原三角形相似,
∴的大小没有发生变化,
∴的值不变,
故选:A.
7.C
【分析】根据正弦三角函数的定义列式计算,本题考查了正弦三角函数的定义,勾股定理,解题的关键是理解正弦三角函数定义.
【详解】,
,
由勾股定理可得,,代入可得:
,
解得,,
故选:.
8.C
【分析】本题主要考查特殊角的三角函数值,掌握根据三角函数值确定三角形的形状是解此题的关键.
根据特殊角的三角函数值,直接得出,的角度即可解答.
【详解】解:,
,
是等腰直角三角形.
故选C.
9.
【分析】本题考查特殊角的三角函数值的运算,解题的关键是熟记特殊角的三角函数值,掌握运算法则.根据特殊角的三角形函数值的运算法则计算即可.
【详解】解:
.
10.35
【分析】本题考查正弦余弦关系.根据题意利用正弦余弦等值则角度互余,即可得到本题答案.
【详解】解:∵,
∴,即:,
故答案为:35.
11.
【分析】本题考查解直角三角形,根据题意设锐角的邻边为a,则对边为,求出斜边长,然后根据余弦等于邻边与斜边的比计算是解题的关键.
【详解】解:设锐角的邻边为a,则对边为,
∴斜边为,
∴,
故答案为:.
12.
【分析】本题主要考查了解直角三角形的应用,解题时要能紧扣问题,借助直角三角形去求解是关键.先得,由,从而求出,最后由进行计算可以得解.
【详解】解:∵,,
∴,
又,
∴,
∴,
故答案为:.
13./
【分析】本题考查三角函数,先得出,再设,,求出,进而得出答案.
【详解】解:∵,
∴,
如图所示:设,,
∴,
∴,
故答案为:.
14.
【分析】本题考查坡度,先利用勾勾股定理求出水平距离,然后利用公式计算是解题的关键.
【详解】解:如图,,,
∴,
∴斜坡的坡度为,
故答案为:.
15.
【分析】本题考查了解直角三角形的应用——仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.根据题意可得:,,然后在中,利用锐角三角函数的定义进行计算即可解答.
【详解】解:由题意得:
,,
在中,米,
(米),
故答案为:.
16.
【分析】此题考查了坡度坡角问题.此题比较简单,注意理解坡度的定义是解此题的关键.根据坡比等于竖直高度与水平长度的比解答即可.
【详解】解:∵迎水坡的坡比为,
∴,
故答案为:.
17.
【分析】本题考查了特殊角三角函数值的混合运算,注意计算的准确性即可.
【详解】解:原式.
18.,,.
【分析】本题考查了解直角三角形,首先根据和的长度得出,继而求出,从而得出和的度数.
【详解】解:如图,在中,,,,
∴
∵,
∴,
∴.
19.,
【分析】本题考查了分式的化简求值以及特殊角的三角函数值,熟记是代值计算的关键.
【详解】解:原式
,
∵
,
∴原式.
20.(1)
(2)
【分析】本题考查解直角三角形的应用;
(1)利用的正切解题即可;
(2)在中运用勾股定理求出长,在中运用角所对的直角边等于斜边的一半求出长即可得到答案.
【详解】(1)解:在中,,
∴;
(2)解:,
在中,,
∴,
∴钢丝的总长度为.
21.(1)点到旗杆的距离约为
(2)旗杆的高度约为
【分析】本题考查了解直角三角形的应用;含直角三角形的性质;
(1)过点作交于点,过点作交于点,利用,,可求出的长度,即可确定点到旗杆的距离;
(2)利用,,可得,在中利用三角函数即可求出、、的长度,在中求出的长度,即可确定旗杆的高度;
【详解】(1)解:如图,
过点作交于点,过点作交于点,
则四边形是矩形,
∴,.
∵斜坡的坡度是,
即:,
设,,
在中,根据勾股定理得,解得,
∴,
∴点到旗杆的距离约为.
(2)
根据平行线的性质得:,
∵,
∴,
在中,
∵,
∴,
∵,
∴,
∴.
在中,
∵,
∴.
∴.
∴旗杆的高度约为.
22.(1)见解析
(2)
【分析】(1)根据四边形ABCD是平行四边形及F是AD中点,E是BC中点,可得四边形AECF是平行四边形,再根据EF平分∠AEC,易证得,则可得,继而证得结论;
(2)过点O作于点G,由三角形面积公式可求的长,勾股定理可求,的长,的长即可求解.
【详解】(1)证明:∵四边形ABCD是平行四边形
∴,
∵F是AD中点,E是BC中点
∴,
∴四边形AECF是平行四边形
∵EF平分∠AEC
∴
∵
∴
∴
∴四边形AECF是菱形
(2)解:∵四边形AECF是菱形
∴,,
∵,,
∴
∴,
过点O作于点G,
∵,
即
∴,
∵
∴,
∴
【点睛】本题考查了平行四边形的性质,菱形的判定和性质,勾股定理的应用,解直角三角形,三角形面积公式的应用,解题的关键是熟练掌握各知识点,作出辅助线,用好数形结合的思想.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学九年级下册北师大版第一章直角三角形的边角关系
一、单选题
1.的相反数是( )
A.1 B. C. D.
2.如图,在中,,,下列用线段比表示的值,错误的是( )
A. B. C. D.
3.如图,在中,,若,,则的值为( )
A. B. C. D.
4.2022年2月4日第24届冬季奥运会在北京举办,某校也开展了丰富多彩的冰雪活动.如图是该校同学参加的冰雪项目学习,小嵩乘滑雪板沿斜坡滑雪道直线滑行,若滑行距离米,斜坡滑雪道与水平面的夹角为,则他下降的高度为( )
A.米 B.米 C.米 D.米
5.下列式子错误的是( )
A. B.
C. D.
6.的边长都扩大2倍,则的值( )
A.不变 B.变大 C.变小 D.无法判断
7.在中,,如果,,那么等于( )
A. B. C. D.
8.如果中,,则下列结论正确的是( )
A.是等边三角形 B.是钝角三角形
C.是等腰直角三角形 D.是锐角三角形
二、填空题
9.计算: .
10.已知锐角满足,则 .
11.已知,锐角的正切值是3,则它的余弦值是 .
12.如图,在中,,于点D,,,那么 .
13.已知为锐角,且,则的值为 .
14.已知一条斜坡的长度为13米,高度为5米,那么该斜坡的坡度为 .
15.如图,小明在点C处测得树的顶端A仰角为,测得米,则树的高(单位:米)为 .
16.河堤横断面如图所示,迎水坡的坡比为,则 .
三、解答题
17.计算:.
18.在中,,,,解这个直角三角形.
19.先化简,再求代数式的值,其中.
20.如图,彩旗旗杆用,两根钢丝固定在地面上,点A,B,C,D在同一平面内,,,,.
(1)求旗杆部分的长.
(2)求钢丝的总长度.(结果保留根号)
21.小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆的影子恰好落在水平地面和斜坡面上,测得旗杆在水平地面上的影长,在斜坡坡面上的影长,太阳光线与水平线所成的角为.
(1)若斜坡的坡度是,求点到旗杆的距离;
(2)若太阳光线与斜坡坡面的夹角为,求旗杆的高度;(精确到1m).(参考数据:,,,,)
22.如图,在中,点E是中点.点F是中点.连接平分.
(1)求证:四边形是菱形:
(2)连接,与交于点O,连接.若,,求的长.
参考答案:
1.B
【分析】本题考查了相反数的定义,特殊角的三角函数值,掌握特殊角的三角函数值是解题的关键.根据特殊角的三角函数值以及相反数的定义即可求解.
【详解】解:∵,
∴的相反数是.
故选:B.
2.D
【分析】本题考查了锐角三角函数关系,正确把握锐角三角函数定义是解题关键.根据锐角三角函数关系的定义分析得出答案.
【详解】解:∵在中,,,
∴,,
∴,
∴.
∴A,B,C正确,不符合题意,D错误,符合题意,
故选:D.
3.D
【分析】本题考查了锐角三角函数的定义,能熟记锐角三角函数的定义是解此题的关键.根据锐角三角函数的定义得出,再代入求出答案即可.
【详解】解:,,,
∴,
故选:D.
4.B
【分析】本题考查的是解直角三角形的应用坡度坡角问题.过点作水平面于点,根据正弦的定义计算即可.
【详解】解:如图,过点作水平面于点,
在中,,米,
,
(米),
故选:B.
5.C
【分析】本题考查三角函数计算.根据题意熟记特殊角三角函数值是解决本题的关键,逐一计算选项即可选出本题答案.
【详解】解:A、∵,故A选项正确;
B、∵,故B选项正确;
C、∵,
∴,故C选项不正确;
D、∵,故D选项正确;
故选:C.
6.A
【分析】本题考查了解直角三角形,熟练掌握锐角三角函数的定义是解题的关键.根据题意可得所得的三角形与原三角形相似,从而可得的大小没有发生变化,即可解答.
【详解】解:∵的边长都扩大2倍,
∴所得的三角形与原三角形相似,
∴的大小没有发生变化,
∴的值不变,
故选:A.
7.C
【分析】根据正弦三角函数的定义列式计算,本题考查了正弦三角函数的定义,勾股定理,解题的关键是理解正弦三角函数定义.
【详解】,
,
由勾股定理可得,,代入可得:
,
解得,,
故选:.
8.C
【分析】本题主要考查特殊角的三角函数值,掌握根据三角函数值确定三角形的形状是解此题的关键.
根据特殊角的三角函数值,直接得出,的角度即可解答.
【详解】解:,
,
是等腰直角三角形.
故选C.
9.
【分析】本题考查特殊角的三角函数值的运算,解题的关键是熟记特殊角的三角函数值,掌握运算法则.根据特殊角的三角形函数值的运算法则计算即可.
【详解】解:
.
10.35
【分析】本题考查正弦余弦关系.根据题意利用正弦余弦等值则角度互余,即可得到本题答案.
【详解】解:∵,
∴,即:,
故答案为:35.
11.
【分析】本题考查解直角三角形,根据题意设锐角的邻边为a,则对边为,求出斜边长,然后根据余弦等于邻边与斜边的比计算是解题的关键.
【详解】解:设锐角的邻边为a,则对边为,
∴斜边为,
∴,
故答案为:.
12.
【分析】本题主要考查了解直角三角形的应用,解题时要能紧扣问题,借助直角三角形去求解是关键.先得,由,从而求出,最后由进行计算可以得解.
【详解】解:∵,,
∴,
又,
∴,
∴,
故答案为:.
13./
【分析】本题考查三角函数,先得出,再设,,求出,进而得出答案.
【详解】解:∵,
∴,
如图所示:设,,
∴,
∴,
故答案为:.
14.
【分析】本题考查坡度,先利用勾勾股定理求出水平距离,然后利用公式计算是解题的关键.
【详解】解:如图,,,
∴,
∴斜坡的坡度为,
故答案为:.
15.
【分析】本题考查了解直角三角形的应用——仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.根据题意可得:,,然后在中,利用锐角三角函数的定义进行计算即可解答.
【详解】解:由题意得:
,,
在中,米,
(米),
故答案为:.
16.
【分析】此题考查了坡度坡角问题.此题比较简单,注意理解坡度的定义是解此题的关键.根据坡比等于竖直高度与水平长度的比解答即可.
【详解】解:∵迎水坡的坡比为,
∴,
故答案为:.
17.
【分析】本题考查了特殊角三角函数值的混合运算,注意计算的准确性即可.
【详解】解:原式.
18.,,.
【分析】本题考查了解直角三角形,首先根据和的长度得出,继而求出,从而得出和的度数.
【详解】解:如图,在中,,,,
∴
∵,
∴,
∴.
19.,
【分析】本题考查了分式的化简求值以及特殊角的三角函数值,熟记是代值计算的关键.
【详解】解:原式
,
∵
,
∴原式.
20.(1)
(2)
【分析】本题考查解直角三角形的应用;
(1)利用的正切解题即可;
(2)在中运用勾股定理求出长,在中运用角所对的直角边等于斜边的一半求出长即可得到答案.
【详解】(1)解:在中,,
∴;
(2)解:,
在中,,
∴,
∴钢丝的总长度为.
21.(1)点到旗杆的距离约为
(2)旗杆的高度约为
【分析】本题考查了解直角三角形的应用;含直角三角形的性质;
(1)过点作交于点,过点作交于点,利用,,可求出的长度,即可确定点到旗杆的距离;
(2)利用,,可得,在中利用三角函数即可求出、、的长度,在中求出的长度,即可确定旗杆的高度;
【详解】(1)解:如图,
过点作交于点,过点作交于点,
则四边形是矩形,
∴,.
∵斜坡的坡度是,
即:,
设,,
在中,根据勾股定理得,解得,
∴,
∴点到旗杆的距离约为.
(2)
根据平行线的性质得:,
∵,
∴,
在中,
∵,
∴,
∵,
∴,
∴.
在中,
∵,
∴.
∴.
∴旗杆的高度约为.
22.(1)见解析
(2)
【分析】(1)根据四边形ABCD是平行四边形及F是AD中点,E是BC中点,可得四边形AECF是平行四边形,再根据EF平分∠AEC,易证得,则可得,继而证得结论;
(2)过点O作于点G,由三角形面积公式可求的长,勾股定理可求,的长,的长即可求解.
【详解】(1)证明:∵四边形ABCD是平行四边形
∴,
∵F是AD中点,E是BC中点
∴,
∴四边形AECF是平行四边形
∵EF平分∠AEC
∴
∵
∴
∴
∴四边形AECF是菱形
(2)解:∵四边形AECF是菱形
∴,,
∵,,
∴
∴,
过点O作于点G,
∵,
即
∴,
∵
∴,
∴
【点睛】本题考查了平行四边形的性质,菱形的判定和性质,勾股定理的应用,解直角三角形,三角形面积公式的应用,解题的关键是熟练掌握各知识点,作出辅助线,用好数形结合的思想.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
