2023-2024学年数学九年级下册北师大版第二章二次函数(含解析)
文档属性
| 名称 | 2023-2024学年数学九年级下册北师大版第二章二次函数(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 18:19:16 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学九年级下册北师大版第二章二次函数
一、单选题
1.在平面直角坐标系中,下列二次函数的图象开口向上的是( )
A. B. C. D.
2.将函数的图象用下列方法平移后,所得的图象经过的是( )
A.向上平移1个单位 B.向下平移2个单位
C.向左平移1个单位 D.向右平移2个单位
3.二次函数的图象的顶点坐标是( )
A. B. C. D.
4.已知二次函数,当时,函数有最小值,则b的值为( )
A.或 B.或 C. D.或
5.某超市销售一种饮料,每瓶进价为4元,经市场调查表明:每瓶售价每增加1元,日均销售量减少80瓶;当售价为每瓶7元时,日均销售量为400瓶,若要日均毛利润最大,每瓶饮料的售价应是( )
A.6元 B.7元 C.8元 D.9元
6.已知点,,是抛物线上的点,则,,的大小关系为( )
A. B. C. D.
7.用总长为米的材料做成如图1的矩形窗框,设窗框的宽为米,窗框的面积为米,关于的函数图象如图2,则的值是( )
A.6 B.7 C.8 D.不能确定
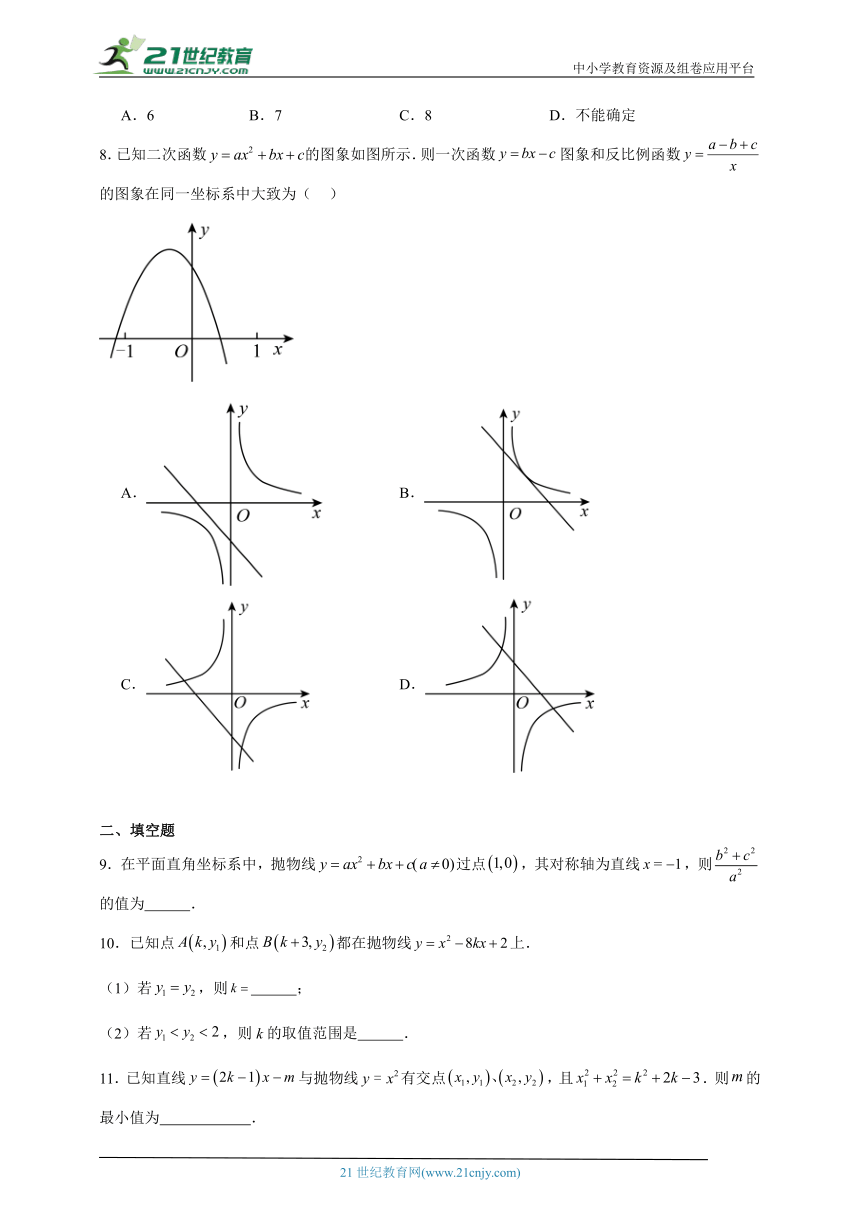
8.已知二次函数的图象如图所示.则一次函数图象和反比例函数的图象在同一坐标系中大致为( )
A. B.
C. D.
二、填空题
9.在平面直角坐标系中,抛物线过点,其对称轴为直线,则的值为 .
10.已知点和点都在抛物线上.
(1)若,则 ;
(2)若,则k的取值范围是 .
11.已知直线与抛物线有交点,且.则的最小值为 .
12.已知二次函数的图象如图所示,则此二次函数的解析式为 .
13.已知二次函数的图象如图所示,则不等式的解集为 .
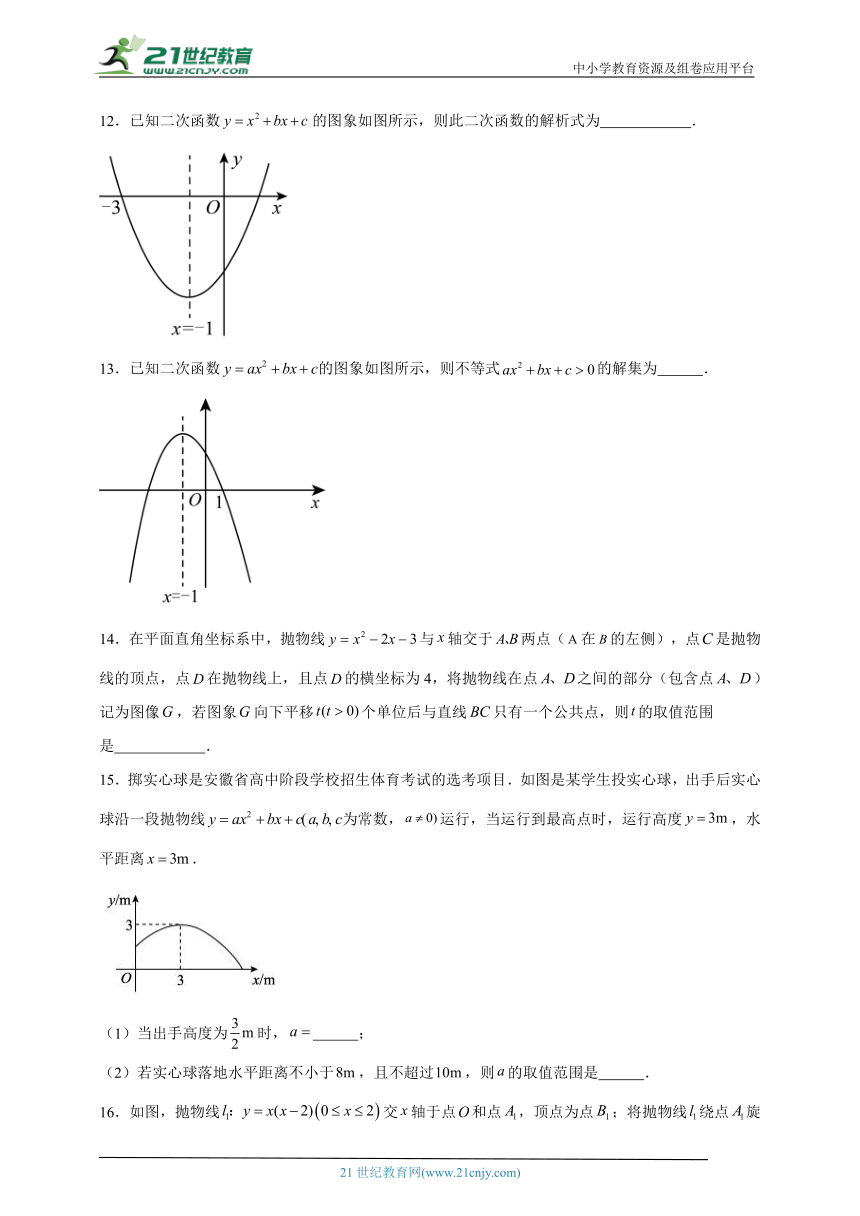
14.在平面直角坐标系中,抛物线与轴交于两点(在的左侧),点是抛物线的顶点,点在抛物线上,且点的横坐标为4,将抛物线在点之间的部分(包含点)记为图像,若图象向下平移个单位后与直线只有一个公共点,则的取值范围是 .
15.掷实心球是安徽省高中阶段学校招生体育考试的选考项目.如图是某学生投实心球,出手后实心球沿一段抛物线为常数,运行,当运行到最高点时,运行高度,水平距离.
(1)当出手高度为时, ;
(2)若实心球落地水平距离不小于,且不超过,则的取值范围是 .
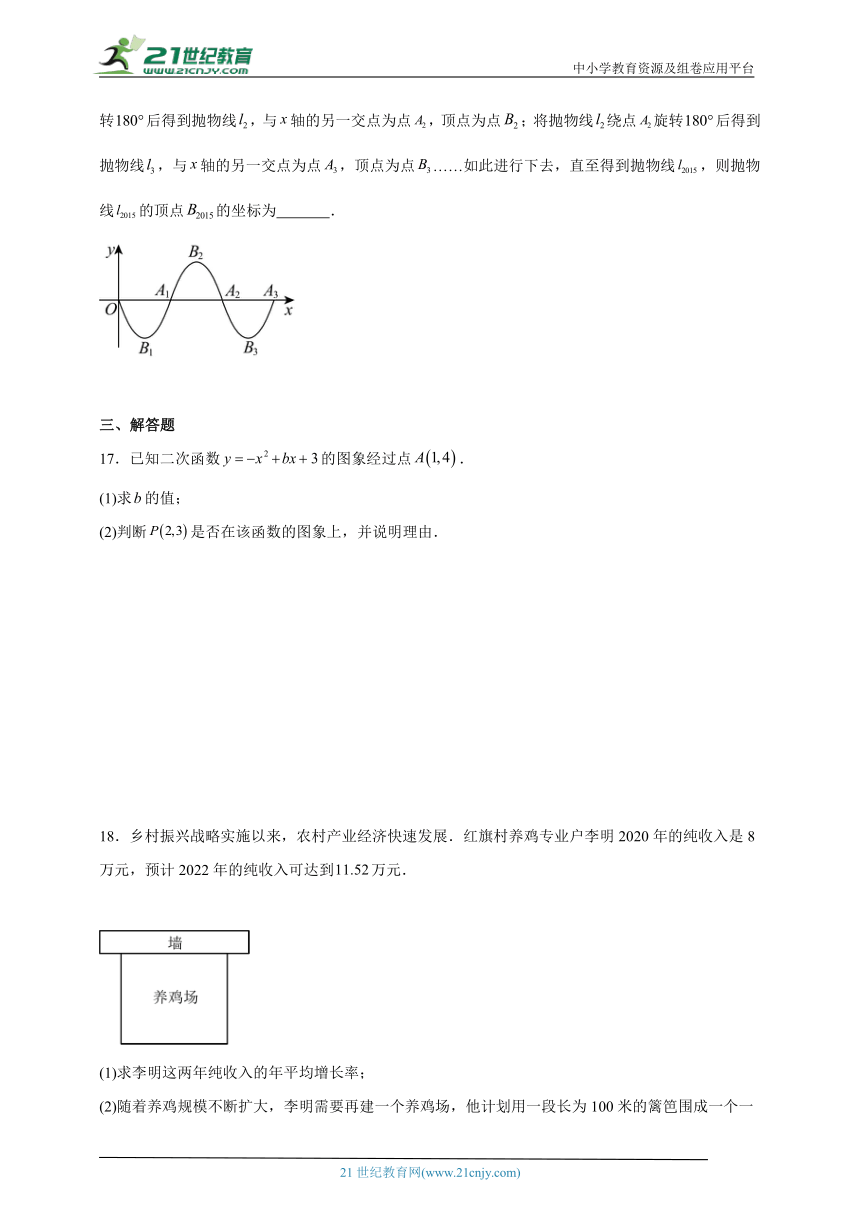
16.如图,抛物线交轴于点和点,顶点为点;将抛物线绕点旋转后得到抛物线,与轴的另一交点为点,顶点为点;将抛物线绕点旋转后得到抛物线,与轴的另一交点为点,顶点为点……如此进行下去,直至得到抛物线,则抛物线的顶点的坐标为 .
三、解答题
17.已知二次函数的图象经过点.
(1)求的值;
(2)判断是否在该函数的图象上,并说明理由.
18.乡村振兴战略实施以来,农村产业经济快速发展.红旗村养鸡专业户李明2020年的纯收入是8万元,预计2022年的纯收入可达到万元.
(1)求李明这两年纯收入的年平均增长率;
(2)随着养鸡规模不断扩大,李明需要再建一个养鸡场,他计划用一段长为100米的篱笆围成一个一边靠墙的矩形养鸡场(如图),墙长60米,要使围成的养鸡场面积最大,则养鸡场与墙平行的一边的长度应是多少米?最大面积是多少米?
19.已知二次函数.
(1)求该二次函数图象的顶点坐标(用含的代数式表示).
(2)点在该二次函数图象上,其中.
①当时,求的取值范围.
②请探究的最大值与最小值之差是否会随着的变化而变化.若不变,请求出这个差;若变化,请用含的代数式表示这个差.
20.已知抛物线:,直线:.
(1)若抛物线的对称轴为直线,且经过点,求该抛物线的解析式;
(2)在(1)的条件下,将抛物线图象轴下方的部分沿轴向上翻折,得到的新图象记作,图象与直线恒有四个交点,从左到右四个交点依次记为,,,,是否存在以为直径的圆恰好过点.若存在,求出的值;若不存在,请说明理由;
(3)若抛物线经过,当,时,对于任意实数,满足恒成立;且当时,恰好有,求直线的解析式.
21.如图1,已知抛物线与x轴交于点,点,与y轴交于点.
(1)求抛物线的解析式;
(2)点M是抛物线对称轴上的点,若最小,求点M的坐标:
(3)如图2,点P是直线BC上方抛物线上一动点(不与B、C重合),若的面积为3,求点P的坐标.
22.如图,某公园的一组同步喷泉由间隔等距的若干个一样的喷泉组成,呈抛物线形的水流从垂直于地面且高出湖面的喷头中向同一侧喷出,每个喷头喷出的水流可看作同样的抛物线.若记水柱上某一位置与喷头的水平距离为,喷出水流与湖面的垂直高度为.
下表中记录了一个喷头喷出水柱时与的几组数据:
0 1 2 3 4.5
1
(1)如图,以喷泉与湖面的交点为原点,建立如图平面直角坐标系,求此抛物线的解析式;
(2)现有一个顶棚为矩形的单人皮划艇,顶棚每一处离湖面的距离为.顶棚刚好接触到水柱,求该皮划艇顶棚的宽度.
(3)现公园管理方准备通过只调节喷头露出湖面的高度,使得游船能从抛物线形水柱下方通过,为避免游客被喷泉淋湿,要求游船从抛物线形水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于,已知游船顶棚宽度为,顶棚到湖面的高度为,那么公园应将喷头(喷头忽略不计)至少向上移动多少才能符合要求?(直接写出结果)
参考答案:
1.C
【分析】本题考查二次函数的图象和性质,二次函数,①当时,抛物线的开口向上;②当时,抛物线的开口向下,据此判断即可.
【详解】解:A、∵,
∴的图象开口向下,故本选项不符合题意;
B、∵,
∴的图象开口向下,故本选项不符合题意;
C、∵,
∴的图象开口向下,故本选项符合题意;
D、∵,
∴的图象开口向下,故本选项不符合题意;
故选:C.
2.C
【分析】考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.根据平移规律,可得答案.
【详解】解:A、平移后,得,图象不经过点,故A不符合题意;
B、平移后,得,图象不经过点,故B不符合题意;
C、平移后,得,图象经过点,故C符合题意;
D、平移后,得,图象不经过点,故D不符合题意;
故选C.
3.C
【分析】本题考查二次函数的性质,懂得从二次函数顶点式中解出顶点坐标是解题的关键.根据题目中函数的解析式即可直接得出此二次函数的顶点坐标.
【详解】解:二次函数的图象的顶点坐标为,
故选:.
4.A
【分析】本题考查二次函数的性质.熟练掌握根据二次函数的最值求系数值是解题的关键.
分三种情况:当时,即时,当时,函数有最小值;当时,即时,当时,函数有最小值;当时,即时,当时,函数有最小值;分别求解即可.
【详解】解:∵,
又∵当时,函数有最小值,
∴当时,即时,当时,函数有最小值,
∴,
解得:,
∴,
当时,即时,当时,函数有最小值,
∴,
解得:;
当时,即时,当时,函数有最小值,
∴,
解得:(舍去),
综上,当时,函数有最小值,b的值为或.
故选:A.
5.C
【分析】本题主要考查了二次函数的实际应用,正确理解题意得出对应的函数关系式是解题的关键.设每瓶的售价为元,日均利润为元,根据列出y关于x的函数关系式,再利用二次函数的性质求解即可.
【详解】解:设每瓶的售价为元,日均利润为元,由题意得;
;
;
∵;
∴当时,y有最大值;
故选:C.
6.D
【分析】本题考查比较二次函数值的大小.理解二次函数当时距离对称轴越远的点,函数值越大是解题关键.先判断函数的开口向上,对称轴为,从而得出距离对称轴越远,函数值越大,再结合三点坐标即可判断函数值之间的大小关系.
【详解】解:抛物线的对称轴为直线,
∵,开口向上,离对称轴越远,函数值越大,
3离对称轴比0离对称轴远,
∴,
故选:D.
7.A
【分析】本题考查了二次函数的应用;根据函数图像,可知当时,窗框的面积最大,最大值为,设窗框的长为,则根据矩形的面积公式,可知,进而根据总长为,即可求得的值.
【详解】解:设窗框的长为,
,
根据函数图像,可知当时,窗框的面积最大,最大值为,
即,
;
故选A.
8.B
【分析】本题考查二次函数的图象与系数的关系,反比例函数及一次函数的性质,熟练掌握以上知识是解题的关键,先根据二次函数的图象开口向下和对称轴可知,由抛物线交轴的正半轴,可知,由当时,,可知,然后利用排除法即可得出正确答案.
【详解】解:∵二次函数的图象开口向下,
∴,
∵,
∴,
∵抛物线交轴的正半轴,
∴,
∴直线经过一、二、三象限,
由图象可知:当时,,
∴,
反比例函数的图象必过一、三象限,
综上所述:A、C、D错误,B正确,
故选:B.
9.
【分析】本题考查了求代数式的值,函数图象上的点,二次函数的对称轴;由已知条件得 ,由二次函数的对称轴得,将代入可求,即可求解;能根据已知条件用表示出、是解题的关键.
【详解】解:抛物线过点,
,
对称轴为直线,
,
,
,
,
;
故答案:.
10. 或
【分析】本题考查了二次函数的性质.(1)先求得抛物线的对称轴为直线,由,得到,据此求解即可;(2)由,求得;由,得到,求得或,据此求解即可.
【详解】解:(1)抛物线的对称轴为直线,
∵,
∴点和点关于直线对称,
∴,
解得,
故答案为:;
(2)当时,
∵,
∴,
解得;
∵,
∴,
整理得,即,
∴或,
解得或,
综上或.
故答案为:或.
11./
【分析】本题考查二次函数的性质,解题关键是掌握二次函数与方程的关系,掌握一元二次方程根与系数的关系.
根据一元二次方程根与系数的关系求得,,然后代入等式,根据二次函数的性质求最值.
【详解】解:当时,,
∴,,
∴,
整理可得,
∵
∴当时,m有最小值为,
故答案为:.
12.
【分析】本题考查利用待定系数法求二次函数的解析式,根据二次函数图象与x轴的交点坐标和对称轴列方程求解即可.
【详解】解:由图象可知,二次函数的图象与x轴的一个交点坐标为,对称轴为直线,
∴,解得,
∴该二次函数的解析式为,
故答案为:.
13.
【分析】本题考查二次函数的图象与x轴的一个交点与不等式的解集的关系.先求出二次函数的图象与x轴的交点,再根据二次函数的图象与x轴的交点,据此即可求解.
【详解】解:由图象可知,二次函数的图象与x轴的一个交点坐标为1,对称轴为,
根据二次函数图象的对称性,可知二次函数的图象与x轴的一个交点坐标为,
∴不等式的解集为,
故答案为:.
14.
【分析】本题考查二次函数的性质、求一次函数的解析式、二次函数图象的平移等知识,利用数形结合思想求解,画出草图,求出临界点对应的t值,结合图象求解即可.
【详解】解:令,由得,,则,,
由得顶点C坐标为,
当时,,则,
画出草图如图:
设直线的解析式为,
则,解得,
∴直线的解析式为,
将图象向下平移个单位后,点A、D对应点坐标为,,
将代入中,得,
将代入中,得,
根据图象,图象向下平移个单位后与直线只有一个公共点,又平移过程中,点比先落在直线上,这时图象G与直线有两个交点,故,
∴的取值范围是,
故答案为:.
15.
【分析】此题考查了二次函数的实际应用,解题的关键是熟练掌握二次函数的性质及其应用;
()利用待定系数法求出解析式即可;
()设,根据当时,,时,即可求出的取值范围.
【详解】解:()设,
将代入可得,
解得,
故答案为:;
(2)设,
若落地水平距离不小于,
则当时,,代入得,解得;
当时,,代入得,解得,
综上所述,.
16.
【分析】本题考查了二次函数的与轴交点坐标问题,求抛物线的顶点坐标等知识.先根据抛物线性质得到抛物线与轴交点坐标为,顶点,进而得到抛物线与轴交点坐标为,顶点;抛物线与轴交点坐标为,顶点;依据规律即可得到抛物线的顶点的坐标.
【详解】解:由题意得抛物线与轴交点坐标为,顶点;
抛物线与轴交点坐标为,顶点;
抛物线与轴交点坐标为,顶点;
……
∴抛物线轴交点的横坐标为,
∴的横坐标为,的纵坐标与的纵坐标相同,为,
∴抛物线的顶点的坐标为.
17.(1)2
(2)是在这个二次函数的图像上,见解析
【分析】本题考查二次函数的解析式,求函数值,待定系数法求二次函数解析式是解题的关键.
(1)把代入求解即可;
(2)把代入二次函数判断即可.
【详解】(1)解:把代入得
,
;
(2)解:当时,
是在这个二次函数的图像上.
18.(1)李明这两年纯收入的年平均增长率为 .
(2)当养鸡场与墙平行的一边的长度应是50米时,养鸡场面积最大值为1250平方米.
【分析】本题主要考查了一元二次方程的实际应用、二次函数的性质等知识点,解题的关键是要理解题意、能正确列出方程和函数解析式成为解题的关键.
(1)设李明这两年纯收入的年平均增长率为x,根据等量关系“李明2020年的纯收入是8万元,预计2022年的纯收入可达到万元”列方程求解即可;
(2)设养鸡场与墙平行的一边的长度为x米且,则可求出与墙垂直的宽为米,再根据长方形的面积公式列出函数解析式,最后根据x的取值范围求最值即可.
【详解】(1)解:设李明这两年纯收入的年平均增长率为x,
根据题意可得:,解得, , (不合题意,舍去)答:李明这两年纯收入的年平均增长率为 .
(2)解:设养鸡场与墙平行的一边的长度为x米且,则可求出与墙垂直的宽为米,
根据题意可得:
养鸡场面积=,
∵,
∴当时,养鸡场面积最大值为1250.
答:当养鸡场与墙平行的一边的长度应是50米时,养鸡场面积最大值为1250平方米.
19.(1)
(2)①;②不变,定值为4
【分析】本题考查了二次函数的性质,二次函数的最值,二次函数图象上点的坐标特征,熟知二次函数的性质是解题的关键.
(1)把解析式化成顶点时,即可求出二次函数图象的顶点坐标;
(2)①当时,则二次函数,,即可求得的取值范围是;
②由题意可知的最小值为,最大值为时的值,即的最大值为,可得的最大值与最小值之差.
【详解】(1)解:,
该二次函数图象的顶点坐标为;
(2)解:①当时,则二次函数,.
,
抛物线开口向上,时有最小值,
当时,,
的取值范围是;
②不变,理由如下:
二次函数的图象开口向上,对称轴为直线,顶点坐标为,
点在该二次函数图象上,其中.
的最小值为,最大值为时的值,
即的最大值为,
的最大值与最小值之差,
的最大值与最小值之差不会随着的变化而变化,的最大值与最小值之差为.
20.(1)
(2)
(3)
【分析】(1)运用待定系数法求出二次函数解析式即可;
(2)由题意可知,图象翻折后得到的函数解析式为: ,对称轴为直线,以为直径的圆过, 可知,将坐标代入翻折后的函数解析式中,求出满足要求的解即可;
(3)根据题意可知为抛物线的顶点,所以,求出符合要求的的值,得到抛物线的解析式与顶点坐标; 由可得 构造函数 当时,随的增大而增大,抛物线顶点恰好在该函数的图象上,可得为抛物线 与的另一个交点横坐标,联立得即化简整理求得的值,进而可得的值,进而可得直线的解析式.
【详解】(1)解:∵抛物线的对称轴为直线,且经过点,
∴,解得,
∴;
(2)解:
∴抛物线的顶点坐标为,
由题意可知,图象翻折后得到的函数解析式为: 对称轴为直线 如图,
∵以为直径的圆恰好过点,若存在,
∴,的中点坐标为,
∴点坐标为,
将代入
解得 或,
∴的值为 ;
(3)∵抛物线经过点, 当,时,对于任意实数,满足恒成立;
∴为抛物线的顶点,
解得 或 ,
,
,
∴抛物线的解析式为:,顶点坐标为,
∵当时,恰好有,
,
, 即 ,
,
,
,
构造函数 当 时, 随的增大而增大,抛物线顶点恰好在该函数的图象上,如图所示,
为抛物线 与 的另一个交点横坐标,
即整理得 解得 (不合题意,舍去),
∴直线的解析式为:
【点睛】本题考查了二次函数解析式,二次函数的图象与性质,二次函数与圆综合,二次函数与反比例函数综合,一次函数解析式等知识.解题的关键在于对知识的熟练掌握与灵活运用.
21.(1)
(2)
(3)或
【分析】本题考查二次函数的综合应用.正确的求出函数解析式,利用数形结合的思想进行求解,是解题的关键.
(1)待定系数法求函数解析式即可;
(2)根据对称性,得到,进而得到当三点共线时,最小,求出的解析式,直线与对称轴的交点即为点;
(3)连接,根据,列出一元二次方程求解即可.
【详解】(1)解:∵抛物线与x轴交于点,点,与y轴交于点,
∴设,把,代入,得:,
∴,
∴;
(2)∵关于对称轴对称,
∴,
∴当三点共线时,最小,
∵,,
∴设直线的解析式为:,把代入,得:,
∴,
∵,
∴对称轴为直线,
∴当时,,
∴;
(3)设点,连接,
由题意,得:
,
解得:或,
∴或.
22.(1)
(2)
(3)公园应将水管高度至少向上调节米才能符合要求.
【分析】本题主要考查了运用待定函数求函数解析式、二次函数图像的平移、二次函数的应用等知识点,将实际问题转化成二次函数问题是解题的关键.
(1)在表格中取三组数据,然后运用待定系数法解答即可;
(2)令,求得对应x的值,然后确定两个x之间的距离即可解答;
(3)设出二次函数图像平移后的解析式,根据题意列出不等式求解即.
【详解】(1)解:由表格可知:函数图像经过点,
设函数解析式为:,
则有:,解得:,
所以函数解析式为:.
(2)解:令,则有,解得:,
所以该皮划艇顶棚的宽度为.
(3)解:设公园应将喷头(喷头忽略不计)至少向上移动才能符合要求,则调节后的水管喷出的抛物线的解析式为:,
∴抛物线的对称轴为:,
由题意可知,当横坐标为时,纵坐标的值不小于,
∴,解得:,
∴水管高度至少向上调节米,
∴公园应将水管高度至少向上调节米才能符合要求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学九年级下册北师大版第二章二次函数
一、单选题
1.在平面直角坐标系中,下列二次函数的图象开口向上的是( )
A. B. C. D.
2.将函数的图象用下列方法平移后,所得的图象经过的是( )
A.向上平移1个单位 B.向下平移2个单位
C.向左平移1个单位 D.向右平移2个单位
3.二次函数的图象的顶点坐标是( )
A. B. C. D.
4.已知二次函数,当时,函数有最小值,则b的值为( )
A.或 B.或 C. D.或
5.某超市销售一种饮料,每瓶进价为4元,经市场调查表明:每瓶售价每增加1元,日均销售量减少80瓶;当售价为每瓶7元时,日均销售量为400瓶,若要日均毛利润最大,每瓶饮料的售价应是( )
A.6元 B.7元 C.8元 D.9元
6.已知点,,是抛物线上的点,则,,的大小关系为( )
A. B. C. D.
7.用总长为米的材料做成如图1的矩形窗框,设窗框的宽为米,窗框的面积为米,关于的函数图象如图2,则的值是( )
A.6 B.7 C.8 D.不能确定
8.已知二次函数的图象如图所示.则一次函数图象和反比例函数的图象在同一坐标系中大致为( )
A. B.
C. D.
二、填空题
9.在平面直角坐标系中,抛物线过点,其对称轴为直线,则的值为 .
10.已知点和点都在抛物线上.
(1)若,则 ;
(2)若,则k的取值范围是 .
11.已知直线与抛物线有交点,且.则的最小值为 .
12.已知二次函数的图象如图所示,则此二次函数的解析式为 .
13.已知二次函数的图象如图所示,则不等式的解集为 .
14.在平面直角坐标系中,抛物线与轴交于两点(在的左侧),点是抛物线的顶点,点在抛物线上,且点的横坐标为4,将抛物线在点之间的部分(包含点)记为图像,若图象向下平移个单位后与直线只有一个公共点,则的取值范围是 .
15.掷实心球是安徽省高中阶段学校招生体育考试的选考项目.如图是某学生投实心球,出手后实心球沿一段抛物线为常数,运行,当运行到最高点时,运行高度,水平距离.
(1)当出手高度为时, ;
(2)若实心球落地水平距离不小于,且不超过,则的取值范围是 .
16.如图,抛物线交轴于点和点,顶点为点;将抛物线绕点旋转后得到抛物线,与轴的另一交点为点,顶点为点;将抛物线绕点旋转后得到抛物线,与轴的另一交点为点,顶点为点……如此进行下去,直至得到抛物线,则抛物线的顶点的坐标为 .
三、解答题
17.已知二次函数的图象经过点.
(1)求的值;
(2)判断是否在该函数的图象上,并说明理由.
18.乡村振兴战略实施以来,农村产业经济快速发展.红旗村养鸡专业户李明2020年的纯收入是8万元,预计2022年的纯收入可达到万元.
(1)求李明这两年纯收入的年平均增长率;
(2)随着养鸡规模不断扩大,李明需要再建一个养鸡场,他计划用一段长为100米的篱笆围成一个一边靠墙的矩形养鸡场(如图),墙长60米,要使围成的养鸡场面积最大,则养鸡场与墙平行的一边的长度应是多少米?最大面积是多少米?
19.已知二次函数.
(1)求该二次函数图象的顶点坐标(用含的代数式表示).
(2)点在该二次函数图象上,其中.
①当时,求的取值范围.
②请探究的最大值与最小值之差是否会随着的变化而变化.若不变,请求出这个差;若变化,请用含的代数式表示这个差.
20.已知抛物线:,直线:.
(1)若抛物线的对称轴为直线,且经过点,求该抛物线的解析式;
(2)在(1)的条件下,将抛物线图象轴下方的部分沿轴向上翻折,得到的新图象记作,图象与直线恒有四个交点,从左到右四个交点依次记为,,,,是否存在以为直径的圆恰好过点.若存在,求出的值;若不存在,请说明理由;
(3)若抛物线经过,当,时,对于任意实数,满足恒成立;且当时,恰好有,求直线的解析式.
21.如图1,已知抛物线与x轴交于点,点,与y轴交于点.
(1)求抛物线的解析式;
(2)点M是抛物线对称轴上的点,若最小,求点M的坐标:
(3)如图2,点P是直线BC上方抛物线上一动点(不与B、C重合),若的面积为3,求点P的坐标.
22.如图,某公园的一组同步喷泉由间隔等距的若干个一样的喷泉组成,呈抛物线形的水流从垂直于地面且高出湖面的喷头中向同一侧喷出,每个喷头喷出的水流可看作同样的抛物线.若记水柱上某一位置与喷头的水平距离为,喷出水流与湖面的垂直高度为.
下表中记录了一个喷头喷出水柱时与的几组数据:
0 1 2 3 4.5
1
(1)如图,以喷泉与湖面的交点为原点,建立如图平面直角坐标系,求此抛物线的解析式;
(2)现有一个顶棚为矩形的单人皮划艇,顶棚每一处离湖面的距离为.顶棚刚好接触到水柱,求该皮划艇顶棚的宽度.
(3)现公园管理方准备通过只调节喷头露出湖面的高度,使得游船能从抛物线形水柱下方通过,为避免游客被喷泉淋湿,要求游船从抛物线形水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于,已知游船顶棚宽度为,顶棚到湖面的高度为,那么公园应将喷头(喷头忽略不计)至少向上移动多少才能符合要求?(直接写出结果)
参考答案:
1.C
【分析】本题考查二次函数的图象和性质,二次函数,①当时,抛物线的开口向上;②当时,抛物线的开口向下,据此判断即可.
【详解】解:A、∵,
∴的图象开口向下,故本选项不符合题意;
B、∵,
∴的图象开口向下,故本选项不符合题意;
C、∵,
∴的图象开口向下,故本选项符合题意;
D、∵,
∴的图象开口向下,故本选项不符合题意;
故选:C.
2.C
【分析】考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.根据平移规律,可得答案.
【详解】解:A、平移后,得,图象不经过点,故A不符合题意;
B、平移后,得,图象不经过点,故B不符合题意;
C、平移后,得,图象经过点,故C符合题意;
D、平移后,得,图象不经过点,故D不符合题意;
故选C.
3.C
【分析】本题考查二次函数的性质,懂得从二次函数顶点式中解出顶点坐标是解题的关键.根据题目中函数的解析式即可直接得出此二次函数的顶点坐标.
【详解】解:二次函数的图象的顶点坐标为,
故选:.
4.A
【分析】本题考查二次函数的性质.熟练掌握根据二次函数的最值求系数值是解题的关键.
分三种情况:当时,即时,当时,函数有最小值;当时,即时,当时,函数有最小值;当时,即时,当时,函数有最小值;分别求解即可.
【详解】解:∵,
又∵当时,函数有最小值,
∴当时,即时,当时,函数有最小值,
∴,
解得:,
∴,
当时,即时,当时,函数有最小值,
∴,
解得:;
当时,即时,当时,函数有最小值,
∴,
解得:(舍去),
综上,当时,函数有最小值,b的值为或.
故选:A.
5.C
【分析】本题主要考查了二次函数的实际应用,正确理解题意得出对应的函数关系式是解题的关键.设每瓶的售价为元,日均利润为元,根据列出y关于x的函数关系式,再利用二次函数的性质求解即可.
【详解】解:设每瓶的售价为元,日均利润为元,由题意得;
;
;
∵;
∴当时,y有最大值;
故选:C.
6.D
【分析】本题考查比较二次函数值的大小.理解二次函数当时距离对称轴越远的点,函数值越大是解题关键.先判断函数的开口向上,对称轴为,从而得出距离对称轴越远,函数值越大,再结合三点坐标即可判断函数值之间的大小关系.
【详解】解:抛物线的对称轴为直线,
∵,开口向上,离对称轴越远,函数值越大,
3离对称轴比0离对称轴远,
∴,
故选:D.
7.A
【分析】本题考查了二次函数的应用;根据函数图像,可知当时,窗框的面积最大,最大值为,设窗框的长为,则根据矩形的面积公式,可知,进而根据总长为,即可求得的值.
【详解】解:设窗框的长为,
,
根据函数图像,可知当时,窗框的面积最大,最大值为,
即,
;
故选A.
8.B
【分析】本题考查二次函数的图象与系数的关系,反比例函数及一次函数的性质,熟练掌握以上知识是解题的关键,先根据二次函数的图象开口向下和对称轴可知,由抛物线交轴的正半轴,可知,由当时,,可知,然后利用排除法即可得出正确答案.
【详解】解:∵二次函数的图象开口向下,
∴,
∵,
∴,
∵抛物线交轴的正半轴,
∴,
∴直线经过一、二、三象限,
由图象可知:当时,,
∴,
反比例函数的图象必过一、三象限,
综上所述:A、C、D错误,B正确,
故选:B.
9.
【分析】本题考查了求代数式的值,函数图象上的点,二次函数的对称轴;由已知条件得 ,由二次函数的对称轴得,将代入可求,即可求解;能根据已知条件用表示出、是解题的关键.
【详解】解:抛物线过点,
,
对称轴为直线,
,
,
,
,
;
故答案:.
10. 或
【分析】本题考查了二次函数的性质.(1)先求得抛物线的对称轴为直线,由,得到,据此求解即可;(2)由,求得;由,得到,求得或,据此求解即可.
【详解】解:(1)抛物线的对称轴为直线,
∵,
∴点和点关于直线对称,
∴,
解得,
故答案为:;
(2)当时,
∵,
∴,
解得;
∵,
∴,
整理得,即,
∴或,
解得或,
综上或.
故答案为:或.
11./
【分析】本题考查二次函数的性质,解题关键是掌握二次函数与方程的关系,掌握一元二次方程根与系数的关系.
根据一元二次方程根与系数的关系求得,,然后代入等式,根据二次函数的性质求最值.
【详解】解:当时,,
∴,,
∴,
整理可得,
∵
∴当时,m有最小值为,
故答案为:.
12.
【分析】本题考查利用待定系数法求二次函数的解析式,根据二次函数图象与x轴的交点坐标和对称轴列方程求解即可.
【详解】解:由图象可知,二次函数的图象与x轴的一个交点坐标为,对称轴为直线,
∴,解得,
∴该二次函数的解析式为,
故答案为:.
13.
【分析】本题考查二次函数的图象与x轴的一个交点与不等式的解集的关系.先求出二次函数的图象与x轴的交点,再根据二次函数的图象与x轴的交点,据此即可求解.
【详解】解:由图象可知,二次函数的图象与x轴的一个交点坐标为1,对称轴为,
根据二次函数图象的对称性,可知二次函数的图象与x轴的一个交点坐标为,
∴不等式的解集为,
故答案为:.
14.
【分析】本题考查二次函数的性质、求一次函数的解析式、二次函数图象的平移等知识,利用数形结合思想求解,画出草图,求出临界点对应的t值,结合图象求解即可.
【详解】解:令,由得,,则,,
由得顶点C坐标为,
当时,,则,
画出草图如图:
设直线的解析式为,
则,解得,
∴直线的解析式为,
将图象向下平移个单位后,点A、D对应点坐标为,,
将代入中,得,
将代入中,得,
根据图象,图象向下平移个单位后与直线只有一个公共点,又平移过程中,点比先落在直线上,这时图象G与直线有两个交点,故,
∴的取值范围是,
故答案为:.
15.
【分析】此题考查了二次函数的实际应用,解题的关键是熟练掌握二次函数的性质及其应用;
()利用待定系数法求出解析式即可;
()设,根据当时,,时,即可求出的取值范围.
【详解】解:()设,
将代入可得,
解得,
故答案为:;
(2)设,
若落地水平距离不小于,
则当时,,代入得,解得;
当时,,代入得,解得,
综上所述,.
16.
【分析】本题考查了二次函数的与轴交点坐标问题,求抛物线的顶点坐标等知识.先根据抛物线性质得到抛物线与轴交点坐标为,顶点,进而得到抛物线与轴交点坐标为,顶点;抛物线与轴交点坐标为,顶点;依据规律即可得到抛物线的顶点的坐标.
【详解】解:由题意得抛物线与轴交点坐标为,顶点;
抛物线与轴交点坐标为,顶点;
抛物线与轴交点坐标为,顶点;
……
∴抛物线轴交点的横坐标为,
∴的横坐标为,的纵坐标与的纵坐标相同,为,
∴抛物线的顶点的坐标为.
17.(1)2
(2)是在这个二次函数的图像上,见解析
【分析】本题考查二次函数的解析式,求函数值,待定系数法求二次函数解析式是解题的关键.
(1)把代入求解即可;
(2)把代入二次函数判断即可.
【详解】(1)解:把代入得
,
;
(2)解:当时,
是在这个二次函数的图像上.
18.(1)李明这两年纯收入的年平均增长率为 .
(2)当养鸡场与墙平行的一边的长度应是50米时,养鸡场面积最大值为1250平方米.
【分析】本题主要考查了一元二次方程的实际应用、二次函数的性质等知识点,解题的关键是要理解题意、能正确列出方程和函数解析式成为解题的关键.
(1)设李明这两年纯收入的年平均增长率为x,根据等量关系“李明2020年的纯收入是8万元,预计2022年的纯收入可达到万元”列方程求解即可;
(2)设养鸡场与墙平行的一边的长度为x米且,则可求出与墙垂直的宽为米,再根据长方形的面积公式列出函数解析式,最后根据x的取值范围求最值即可.
【详解】(1)解:设李明这两年纯收入的年平均增长率为x,
根据题意可得:,解得, , (不合题意,舍去)答:李明这两年纯收入的年平均增长率为 .
(2)解:设养鸡场与墙平行的一边的长度为x米且,则可求出与墙垂直的宽为米,
根据题意可得:
养鸡场面积=,
∵,
∴当时,养鸡场面积最大值为1250.
答:当养鸡场与墙平行的一边的长度应是50米时,养鸡场面积最大值为1250平方米.
19.(1)
(2)①;②不变,定值为4
【分析】本题考查了二次函数的性质,二次函数的最值,二次函数图象上点的坐标特征,熟知二次函数的性质是解题的关键.
(1)把解析式化成顶点时,即可求出二次函数图象的顶点坐标;
(2)①当时,则二次函数,,即可求得的取值范围是;
②由题意可知的最小值为,最大值为时的值,即的最大值为,可得的最大值与最小值之差.
【详解】(1)解:,
该二次函数图象的顶点坐标为;
(2)解:①当时,则二次函数,.
,
抛物线开口向上,时有最小值,
当时,,
的取值范围是;
②不变,理由如下:
二次函数的图象开口向上,对称轴为直线,顶点坐标为,
点在该二次函数图象上,其中.
的最小值为,最大值为时的值,
即的最大值为,
的最大值与最小值之差,
的最大值与最小值之差不会随着的变化而变化,的最大值与最小值之差为.
20.(1)
(2)
(3)
【分析】(1)运用待定系数法求出二次函数解析式即可;
(2)由题意可知,图象翻折后得到的函数解析式为: ,对称轴为直线,以为直径的圆过, 可知,将坐标代入翻折后的函数解析式中,求出满足要求的解即可;
(3)根据题意可知为抛物线的顶点,所以,求出符合要求的的值,得到抛物线的解析式与顶点坐标; 由可得 构造函数 当时,随的增大而增大,抛物线顶点恰好在该函数的图象上,可得为抛物线 与的另一个交点横坐标,联立得即化简整理求得的值,进而可得的值,进而可得直线的解析式.
【详解】(1)解:∵抛物线的对称轴为直线,且经过点,
∴,解得,
∴;
(2)解:
∴抛物线的顶点坐标为,
由题意可知,图象翻折后得到的函数解析式为: 对称轴为直线 如图,
∵以为直径的圆恰好过点,若存在,
∴,的中点坐标为,
∴点坐标为,
将代入
解得 或,
∴的值为 ;
(3)∵抛物线经过点, 当,时,对于任意实数,满足恒成立;
∴为抛物线的顶点,
解得 或 ,
,
,
∴抛物线的解析式为:,顶点坐标为,
∵当时,恰好有,
,
, 即 ,
,
,
,
构造函数 当 时, 随的增大而增大,抛物线顶点恰好在该函数的图象上,如图所示,
为抛物线 与 的另一个交点横坐标,
即整理得 解得 (不合题意,舍去),
∴直线的解析式为:
【点睛】本题考查了二次函数解析式,二次函数的图象与性质,二次函数与圆综合,二次函数与反比例函数综合,一次函数解析式等知识.解题的关键在于对知识的熟练掌握与灵活运用.
21.(1)
(2)
(3)或
【分析】本题考查二次函数的综合应用.正确的求出函数解析式,利用数形结合的思想进行求解,是解题的关键.
(1)待定系数法求函数解析式即可;
(2)根据对称性,得到,进而得到当三点共线时,最小,求出的解析式,直线与对称轴的交点即为点;
(3)连接,根据,列出一元二次方程求解即可.
【详解】(1)解:∵抛物线与x轴交于点,点,与y轴交于点,
∴设,把,代入,得:,
∴,
∴;
(2)∵关于对称轴对称,
∴,
∴当三点共线时,最小,
∵,,
∴设直线的解析式为:,把代入,得:,
∴,
∵,
∴对称轴为直线,
∴当时,,
∴;
(3)设点,连接,
由题意,得:
,
解得:或,
∴或.
22.(1)
(2)
(3)公园应将水管高度至少向上调节米才能符合要求.
【分析】本题主要考查了运用待定函数求函数解析式、二次函数图像的平移、二次函数的应用等知识点,将实际问题转化成二次函数问题是解题的关键.
(1)在表格中取三组数据,然后运用待定系数法解答即可;
(2)令,求得对应x的值,然后确定两个x之间的距离即可解答;
(3)设出二次函数图像平移后的解析式,根据题意列出不等式求解即.
【详解】(1)解:由表格可知:函数图像经过点,
设函数解析式为:,
则有:,解得:,
所以函数解析式为:.
(2)解:令,则有,解得:,
所以该皮划艇顶棚的宽度为.
(3)解:设公园应将喷头(喷头忽略不计)至少向上移动才能符合要求,则调节后的水管喷出的抛物线的解析式为:,
∴抛物线的对称轴为:,
由题意可知,当横坐标为时,纵坐标的值不小于,
∴,解得:,
∴水管高度至少向上调节米,
∴公园应将水管高度至少向上调节米才能符合要求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
