北师大版2024年九年级下册开学数学巩固试题2(含解析)
文档属性
| 名称 | 北师大版2024年九年级下册开学数学巩固试题2(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 15:34:24 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024年九年级开学数学巩固2
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.(2023上·广东深圳·九年级深圳外国语学校校考阶段练习)已知的半径为,,则点和的位置关系是( )
A.点在圆内 B.点在圆上 C.点在圆外 D.无法判断
2.(2023上·广东深圳·九年级校考阶段练习)如图,是的外接圆,,若的半径为6,则弦的长为( )
A.6 B. C. D.
3.(2023上·广东深圳·九年级校考阶段练习)如图,在中,,劣弧的度数是( )
A. B. C. D.
4.(2022上·广东深圳·八年级深圳市高级中学校考期中)在同一直角坐标系中,二次函数与一次函数的图象关系可能是( )
A. B. C. D.
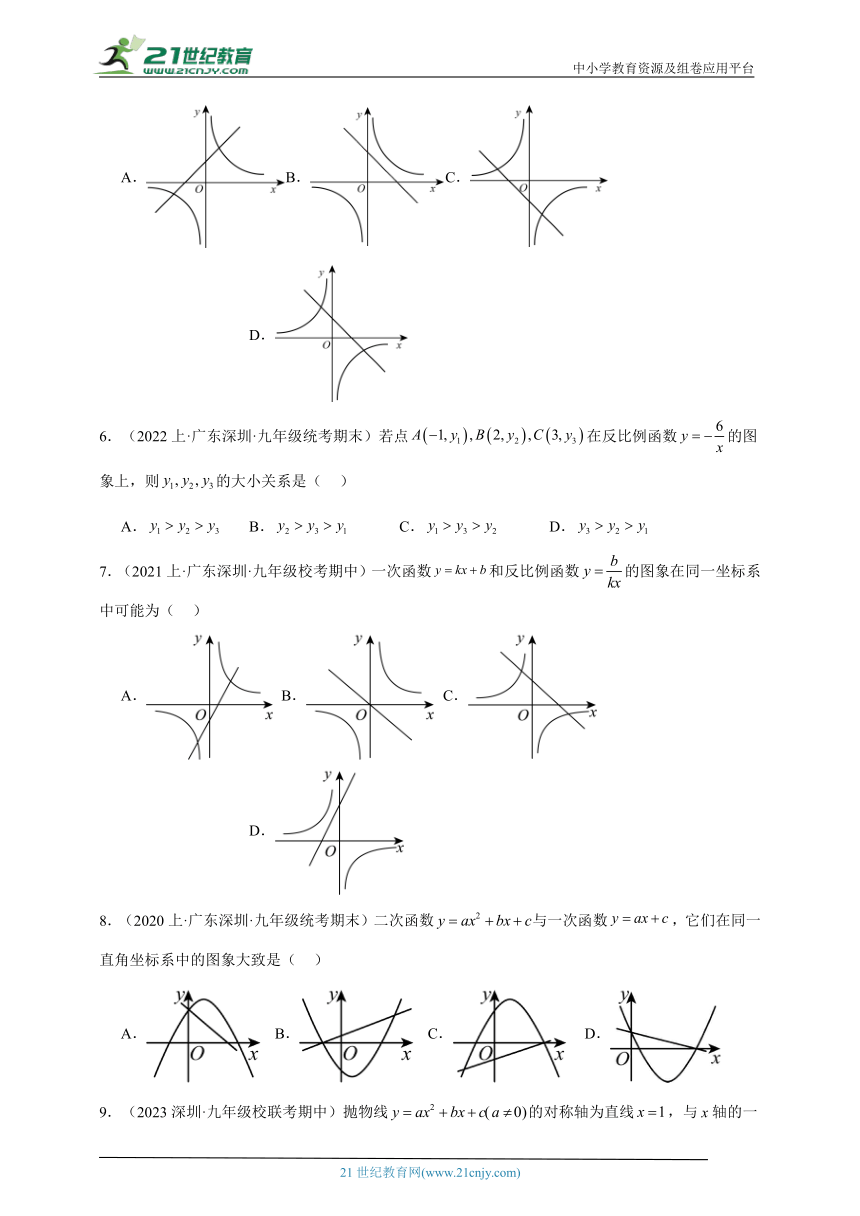
5.(2023上·广东深圳·九年级校考期中)在同一平面直角坐标系中,函数与的大致图象可能是( )
A.B.C. D.
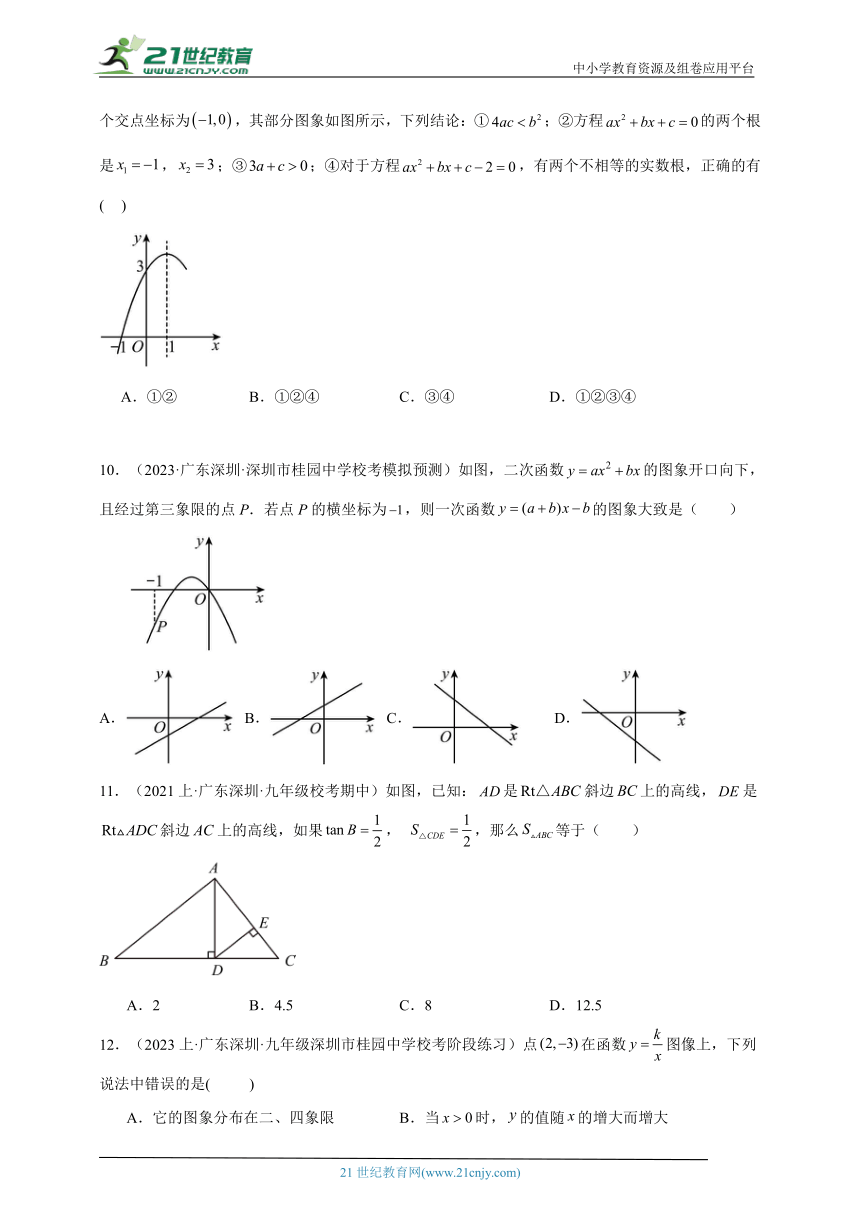
6.(2022上·广东深圳·九年级统考期末)若点在反比例函数的图象上,则的大小关系是( )
A. B. C. D.
7.(2021上·广东深圳·九年级校考期中)一次函数和反比例函数的图象在同一坐标系中可能为( )
A. B. C. D.
8.(2020上·广东深圳·九年级统考期末)二次函数与一次函数,它们在同一直角坐标系中的图象大致是( )
A. B. C. D.
9.(2023深圳·九年级校联考期中)抛物线的对称轴为直线,与x轴的一个交点坐标为,其部分图象如图所示,下列结论:①;②方程的两个根是,;③;④对于方程,有两个不相等的实数根,正确的有( )
①② B.①②④ C.③④ D.①②③④
10.(2023·广东深圳·深圳市桂园中学校考模拟预测)如图,二次函数的图象开口向下,且经过第三象限的点P.若点P的横坐标为,则一次函数的图象大致是( )
A. B. C. D.
11.(2021上·广东深圳·九年级校考期中)如图,已知:是斜边上的高线,是斜边上的高线,如果, ,那么等于( )
A.2 B.4.5 C.8 D.12.5
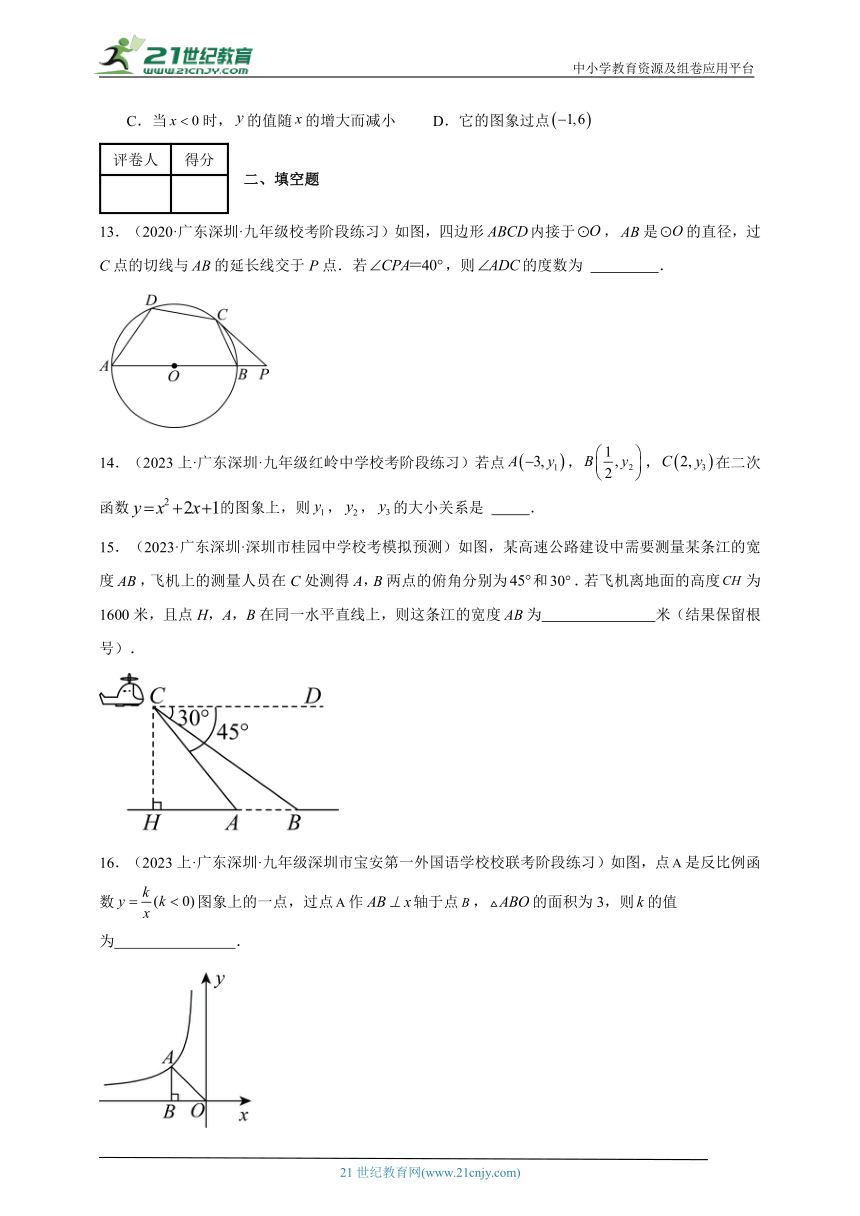
12.(2023上·广东深圳·九年级深圳市桂园中学校考阶段练习)点在函数图像上,下列说法中错误的是( )
A.它的图象分布在二、四象限 B.当时,的值随的增大而增大
C.当时,的值随的增大而减小 D.它的图象过点
评卷人得分
二、填空题
13.(2020·广东深圳·九年级校考阶段练习)如图,四边形内接于,是的直径,过C点的切线与的延长线交于P点.若,则的度数为 .
14.(2023上·广东深圳·九年级红岭中学校考阶段练习)若点,,在二次函数的图象上,则,,的大小关系是 .
15.(2023·广东深圳·深圳市桂园中学校考模拟预测)如图,某高速公路建设中需要测量某条江的宽度,飞机上的测量人员在C处测得A,B两点的俯角分别为和.若飞机离地面的高度为1600米,且点H,A,B在同一水平直线上,则这条江的宽度为 米(结果保留根号).
16.(2023上·广东深圳·九年级深圳市宝安第一外国语学校校联考阶段练习)如图,点是反比例函数图象上的一点,过点作轴于点,的面积为3,则的值为 .
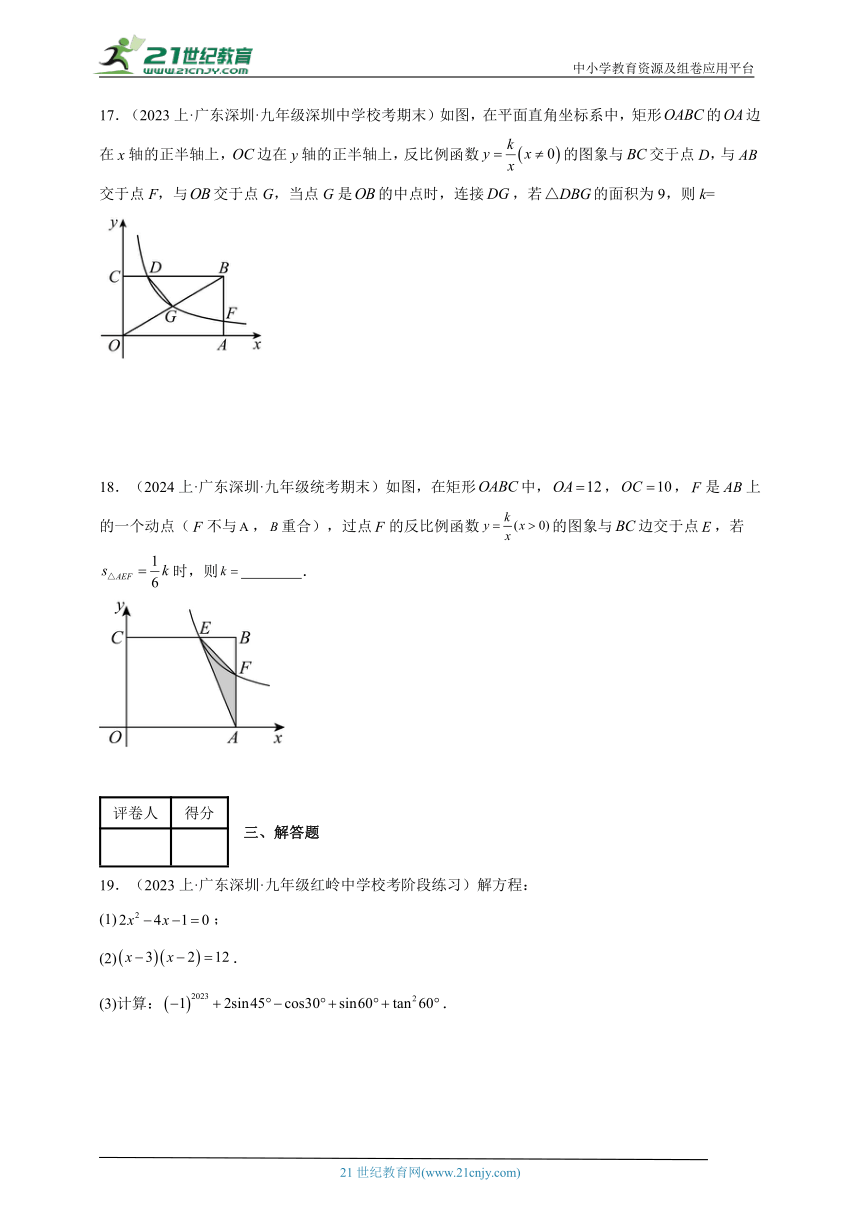
17.(2023上·广东深圳·九年级深圳中学校考期末)如图,在平面直角坐标系中,矩形的边在x轴的正半轴上,边在y轴的正半轴上,反比例函数的图象与交于点D,与交于点F,与交于点G,当点G是的中点时,连接,若的面积为9,则k=
18.(2024上·广东深圳·九年级统考期末)如图,在矩形中,,,是上的一个动点(不与,重合),过点的反比例函数的图象与边交于点,若时,则 .
评卷人得分
三、解答题
19.(2023上·广东深圳·九年级红岭中学校考阶段练习)解方程:
(1);
(2).
(3)计算:.
(2023上·广东深圳·九年级校考阶段练习)
(1)解方程:.
(2)计算:.
(2022上·广东深圳·九年级深圳实验学校中学部校考阶段练习)
(1)计算:;
(2)解方程:.
22.(2022上·深圳·八年级深圳市高级中学校考期中)某市粮库要把晾晒场上的600吨大米入库封存.
(1)求入库所需的时间t(单位:天)与入库速度v(单位:吨/天)的函数关系式;
(2)粮库有职工 40 名,每人每天最多可将吨大米入库,预计将全部大米入库最快可在多少天内完成?
(3)粮库的职工连续工作了 25 天后,上级主管部门决定临时把剩下的大米全部入库,以便尽早调出出售,则至少需要增加多少名人员帮忙才能完成任务?
23.(2023上·广东深圳·九年级深圳市南山区华侨城中学校考阶段练习)如图,在平面直角坐标系中,已知反比例函数与一次函数的图象相交于点和.
(1)分别求反比例函数和一次函数的表达式;
(2)请直接写出当时,的解集.
24.(2022下·广东深圳·九年级校考周测)如图,在中,点是边上一点,以为直径的半圆经过点,点是弦上一点,过点作,垂足为,交的延长线于点,且.
(1)求证:直线与半圆相切;
(2)若已知,求的值.
25.(2023上·广东深圳·九年级校考阶段练习)如图,是的直径,E,C是上两点,且,连接,.过点C作交的延长线于点D.
(1)判定直线与的位置关系,并说明理由;
(2)连接和交于点F,若,,
①求证:四边形是矩形;
②求图中阴影部分的面积.
26.(2023·广东深圳·模拟预测)要修建一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,记喷出的水与池中心的水平距离为x m,距地面的高度为y m.测量得到如下数值:
x/m 0 0.5 1 1.5 2 2.5 3 3.37
y/m 2.44 3.15 3.49 3.45 3.04 2.25 1.09 0
小腾根据学习函数的经验,发现y是x的函数,并对y随x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)在平面直角坐标系xOy中,描出表中各组数值所对应的点,并画出函数的图象;
(2)结合函数图象,出水口距地面的高度为_______m,水达到最高点时与池中心的水平距离约为_______m(结果保留小数点后两位);
(3)为了使水柱落地点与池中心的距离不超过3.2m,如果只调整水管的高度,其他条件不变,结合函数图象,估计出水口至少需要_______(填“升高”或“降低”)_______m(结果保留小数点后两位).
27.(2023上·广东深圳·九年级深圳外国语学校校联考阶段练习)某公园内人工湖上有一座拱桥(横截面如图所示),跨度为米.在距点水平距离为米的地点,拱桥距离水面的高度为米.小红根据学习函数的经验,对和之间的关系进行了探究.
(1)经过测量,得出了和的几组对应值,如表.
米
米
请求出拱桥距离水面的高度与之间的函数关系式,画出确定的函数的图象;
(2)结合表格数据和函数图象,解决问题:
①桥墩露出水面的高度为 米;
②公园欲开设游船项目,现有长为米,宽为米,露出水面高度为米的游船.为安全起见,公园要在水面上的,两处设置警戒线,并且,要求游船能从,两点之间安全通过,则处距桥墩的距离至少为 米.(精确到米)
28.(2023上·广东深圳·九年级校考阶段练习)随着国家乡村振兴政策的推进,凤凰村农副产品越来越丰富,为增加该村村民收入,计划定价销售某土特产,他们把该土特产(每袋成本10元)进行4天试销售,日销量y(袋)和每袋售价x(元)记录如下:
时间 第一天 第二天 第三天 第四天
x/元 15 20 25 30
y/袋 25 20 15 10
若试销售和正常销售期间,日销量y与每袋售价x的一次函数关系相同,解决下列问题:
(1)求日销量y关于每袋售价x的函数关系式;
(2)请你帮村民设计,每袋售价定为多少元,才能使这种土特产每日销售的利润最大?并求出最大利润.(利润=销售额-成本)
29.(2023上·广东深圳·九年级深圳市桂园中学校考阶段练习)消防车是救援火灾的重要装备.图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂可伸缩,伸缩范围为,且起重臂可绕点A在一定范围内转动,张角为,张角范围为,转动点A距离地面的高度为(参考数据:)
(1)当起重臂长度为,张角为时,求云梯消防车最高点B距地面的高度;(结果保留根号)
(2)某栋楼高,若该楼中有居民家突发险情,请问该消防车能否实施有效救援?请说明理由.
30.(2023上·广东深圳·八年级深圳市海湾中学校考期中)综合与实践
【问题情境】某消防队在一次应急演练中,消防员架起一架长的云梯,如图,云梯斜靠在一面墙上,这时云梯底端距墙脚的距离,.
(1)【独立思考】这架云梯顶端距地面的距离有多高?
(2)【深入探究】消防员接到命令,按要求将云梯从顶端下滑到位置上(云梯长度不改变),,那么它的底部在水平方向滑动到的距离也是吗?若是,请说明理由;若不是,请求出的长度.
(3)【问题解决】在演练中,高的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的,则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达高的墙头去救援被困人员?
31.(2021上·广东深圳·九年级校考期中)如图,中,,,.
(1)请画出将向右平移8个单位长度后的;
(2) ;
(3)以O为位似中心,将缩小为原来的,得到,请在y轴右侧画出并直接写出的坐标.
32.(2023上·广东深圳·九年级校考期中)(1)如图1,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点和.
①直接写出____,____,____;
②请直接写出不等式的解集____;连接、,则_______.
(2)如图 2,直线 与 x,y轴分别交于 A、B 两点,点 M是双曲上一点,分别连接、.在双曲线上是否存在点 M,使得以为斜边的与相似?若存在,请求出点 M 的坐标; 若不存在,请说明理由.
33.(2023·广东深圳·南山实验教育集团南海中学校考三模)如图,为的直径,为上一点,与过点的切线互相垂直,垂足为点,交于点,连接,.
(1)求证:;
(2)若,,求的长.
34.(2023·广东深圳·校考模拟预测)请结合图像完成下列问题:
(1)请在图中画出函数:的图像;
(2)结合图像直接写出方程:的解为:_______;
(3)在图中画出函数的图像,并结合图像直接写出方程:的解为: .
35.(2023上·广东深圳·九年级校考阶段练习)视力表中蕴含着很多数学知识,如:每个“E”形图都是正方形结构,同一行的“E”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表.
素材1 国际通用的视力表以5米为检测距离,任选视力表中7个视力值n,测得对应行的“E”形图边长b(mm),在平面直角坐标系中描点如图1.
探究1 检测距离为5米时,归纳n与b的关系式,并求视力值1.2所对应行的“E”形图边长.
素材2 图2为视网膜成像示意图,在检测视力时,眼睛能看清最小“E”形图所成的角叫做分辨视角,视力值与分辨视角(分)的对应关系近似满足.
探究2 当时,属于正常视力,根据函数增减性写出对应的分辨视角的范围.
素材3 如图3,当确定时,在A处用边长为的I号“E”测得的视力与在B处用边长为的Ⅱ号“E”测得的视力相同.
探究3 若检测距离为3米,求视力值1.2所对应行的“E”形图边长.
参考答案:
1.C
【分析】本题主要考查了点与圆的位置关系,根据“若点与圆心的距离d,圆的半径为,则当时,点在圆外;当时,点在圆上;当时,点在圆内”,即可求解.
【详解】解:∵的半径为,,
∴的半径,
∴点和的位置关系是点在圆外.
故选:C
2.B
【分析】此题考查了圆周角定理,勾股定理,首先根据圆周角定理得到,然后利用勾股定理求解即可.解题的关键是熟练掌握圆周角定理(同弧所对的圆心角是圆周角的两倍)和勾股定理(若直角三角形的两条直角边为a和b,斜边为c,则).
【详解】∵
∴
∵的半径为6,
∴
∴.
故选:B.
3.D
【分析】本题考查了弧所对的度数求解,只需求出弧所对的圆心角度数即可.连接,根据结合即可求出.
【详解】解:连接,如图所示:
则
∵,
∴
∴
故劣弧的度数是
故选:D
4.C
【分析】根据题意得:二次函数的图象与x轴的对称点为,再结合二次函数与一次函数的图象,确定a,b的取值范围,即可求解.
【详解】解:根据题意得:二次函数的图象与x轴的对称点为,
A、观察一次函数的图象得,由二次函数的图象得,则,矛盾,故本选项不符合题意;
B、观察一次函数的图象得,由二次函数的图象得,矛盾,故本选项不符合题意;
C、观察一次函数的图象得,由二次函数的图象得,则,相一致,故本选项符合题意;
D、观察一次函数的图象得,由二次函数的图象得,矛盾,故本选项不符合题意;
故选:C
5.D
【分析】本题主要考查了反比例函数的图象和一次函数的图象,熟悉两函数中k的符号对函数图象的影响是解题的关键.
【详解】解:①当时,过一、三、四象限;位于一、三象限;
②当时,过一、二、四象象限;位于二、四象限.
观察图形可知,只有D选项符合题意.
故选D.
6.C
【分析】本题主要考查了比较反比例函数值的大小,根据解析式判断出反比例函数图象经过第二、四象限,且在每个象限内y随x增大而增大是解题的关键.
【详解】解:∵反比例函数解析式为,,
∴反比例函数图象经过第二、四象限,且在每个象限内y随x增大而增大,
∵点在反比例函数的图象上,,
∴,
故选C.
7.C
【分析】此题考查反比例函数和一次函数的图象共存问题;结合图象分别分析一次函数与反比例函数中,的符号,得出一致的符合题意,得出矛盾的不符合题意,从而可得答案.
【详解】解:A选项:由反比例函数的性质知k、b同号,由一次函数图象得,,得k、b异号.两者不一致,故A不符合题意;
B选项:由反比例函数的性质知k、b同号,由一次函数图象得,,两者不一致,故B不符合题意;
C选项:由反比例函数的性质知k、b异号,由一次函数图象得,,k、b异号,两者一致,故C符合题意;
D选项:由反比例函数的性质知k、b异号,由一次函数图象得,,k、b同号,两者不一致.故D不符合题意;
故选C
8.A
【分析】利用二次函数和一次函数图象的性质“二次函数和一次函数的常数项是图象与y轴交点的纵坐标;一次函数的一次项系数大于0,图象经过一、三象限;小于0,经过二、四象限;二次函数的二次项系数大于0,图象开口向上;二次项系数小于0,图象开口向下.”逐项判断即可.
【详解】A.图象中二次函数,一次函数,故A符合题意.
B.图象中二次函数,一次函数,故B不符合题意.
C.图象中二次函数,一次函数,故C不符合题意.
D.图象中二次函数,一次函数,故D不符合题意.
故选:A.
【点睛】本题考查二次函数及一次函数的图象的性质.熟练掌握二次函数和一次函数的图象的性质是解答本题的关键.
9.B
【分析】本题考查了二次函数、一元二次方程、二元一次方程组的知识;根据题意,得时,;结合二次函数对称轴的性质,根据函数图象以及对称轴,即可得到抛物线与轴的交点,再根据二次函数图像的性质分析,即可完成求解.
【详解】根据题意,时,
∵抛物线的对称轴为直线,
∴.
∵抛物线与轴的一个交点坐标为
∴另一个交点为,
∵抛物线与轴有2个交点,
∴
∴成立,
∴①正确;
∴方程的两个根是,,
∴②正确;
∵图象与x轴交于点,
∴
∴③不正确;
∵对于方程,有两个不相等的实数根,
观察函数图象,可得与 有2个交点,
∴④正确;
∴结论正确的是①②④
故选:B.
10.C
【分析】根据二次函数的图象可以判断a、b的正负情况,从而可以得到一次函数经过哪几个象限即可.
【详解】解:由二次函数的图象可知,,
对称轴在y轴左侧,左同右异,,
∴,一次函数与y轴正半轴有交点,
故选:C.
【点睛】本题考查二次函数的性质、一次函数的性质,解答本题的关键是明确题意,利用函数的思想解答.
11.D
【分析】本题考查了解直角三角形的应用,相似三角形的判定与性质,设,先证明,根据等角的正切值相等可得,再证明,根据相似三角形面积比等于相似比的平方即可得出结论.
【详解】解:∵,
∴
设,,
∵,,
∴,
∴,,
∴,
∴,
∴,
∴.
∵,
∴,
∵,
∴,
∴,
∵,
∴,
故选:D.
12.C
【分析】此题主要考查了反比例函数的图象性质,先把点代入,求得,根据反比例函数的性质:当,双曲线的两支分别位于第二、第四象限,在每一象限内随的增大而增大,图象既是轴对称图形又是中心对称图形进行判断即可.
【详解】解:把点代入,得
,
解得:,
∴,
A、∵,∴的图象分布在二、四象限,原说法正确,故此选项不符合题意;
B、∵,∴当时,的值随的增大而增大,原说法正确,故此选项不符合题意;
C、∵,∴当时,的值随的增大而增大,原说法错误,故此选项符合题意;
D、∵把代入,得,∴它的图象过点,原说法正确,故此选项不符合题意;
故选:C.
13./115度
【分析】根据过C点的切线与的延长线交于P点,,连接点C和圆心O,可以求得和的度数,又根据圆内接四边形对角互补,可以求得的度数,本题得以解决.本题考查切线的性质、圆内接四边形对角互补,解题的关键是连接圆心和切点,构造直角三角形,求出四边形的一个角,找出所求问题需要的条件.
【详解】解:连接,如图所示,
由题意可得,,
,
,
,
∵四边形是圆内接四边形,
,
,
故答案为:.
14.
【分析】本题考查了二次函数的性质,根据图象上的点的横坐标距离对称轴的远近来判断纵坐标的大小,解题的关键是熟练掌握二次函数的增减性.
【详解】解:由题知,抛物线的开口向上,且对称轴是直线,
∴函数图象上的点,离对称轴越近,函数值越小,
∵,
∴,
故答案为:.
15.
【分析】由题意易得,然后根据米及三角函数可求解.
【详解】解:由题意可得:,
∵,
∴,
∵米
∴(米),
(米),
∴米.
故答案为:.
【点睛】本题主要考查解直角三角形,熟练掌握三角函数的定义是解题的关键.
16.
【分析】本题考查了反比例函数的性质、反比例函数值的几何意义,由题意得,再根据反比例函数的图象在第二象限,即可得出,熟练掌握反比例函数值的几何意义是解此题的关键.
【详解】解:由题意得:,
,
反比例函数的图象在第二象限,
,
,
故答案为:.
17.12
【分析】连接,根据题意以及反比例函数系数k的几何意义得到,从而表示出矩形的面积,设设,则,最后列出方程求解即可.
【详解】解∶连接OD,
∵矩形的边在x轴的正半轴上,边在y轴的正半轴上,矩形交反比例函数于点D、F,
∴,
∵点G是的中点,的面积为9,
∴,
∴,
∴,
∴矩形的面积为,
设,则,
∴,
解得,
故答案为∶12.
【点睛】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,矩形的性质,三角形的面积,能用含k的式子表示出矩形的面积以及点B的坐标是解题的关键.
18.80
【分析】本题考查了反比例函数的几何意义的应用,三角形面积的同底问题的应用.连接,利用同底面积比等于高之比,得到点坐标,再利用反比例函数的关系式的求法计算即可.
【详解】解:连接,
由题意得:,
,
,
,,
,
,
,
.
故答案为:80.
19.(1),
(2),
(3)
【分析】此题考查了解一元二次方程,特殊角的三角函数值.
(1)利用配方法解方程即可;
(2)利用因式分解法解方程即可;
(3)根据有理数的乘方、特殊角的三角函数值化简,然后进行二次根式的加减运算即可.
【详解】(1)解:,
移项,得,
除以2,得,
配方,得,
即,
开方得,
解得:,;
(2)解:,
整理得:,
,
或,
解得:,;
(3)解:原式
.
20.(1),;(2)0
【分析】本题考查解一元二次方程,特殊角三角函数的混合运算:
(1)利用配方法或公式法求解;
(2)将特殊角三角函数值代入计算即可.
【详解】解:(1),
,
,
,
,
,
解得,.
(2)
21.(1);(2),
【分析】本题主要考查负指数幂,特殊角的三角函数值的计算,绝对值的性质,因式分解求一元二次方程,掌握实数的计算方法,因式分解法求一元二次方程的解是解题的关键.
(1)先算负指数幂,特殊角的三角函数值,绝对值的化简,再根据实数的混合运算法则即可求解;
(2)移项,提取公因式进行因数分解即可求解.
【详解】解:(1)
;
(2)
移项得,
提取公因式得,,整理得,
∴或,
∴,.
22.(1)
(2)30
(3)160人
【分析】(1)根据工作时间工作总量工作效率可得函数关系式;
(2)直接把代入解析式求解即可;
(3)根据题意求出剩余的玉米一天内全部入库需职工人数为200人,所以需增加的人数即可求出.
【详解】(1)解:根据关系式:工作时间工作总量工作效率可得:
入库所需的时间 t 与入库速度 v 的函数关系式为;
(2)根据题意得:,
∴预计将全部大米入库最快可在30天内完成;
(3)粮库的职工连续工作了25天的入库量为,
由题可知:剩下的粮食需要再一天内完成入库,
则所需人数为 (人),
(人).
【点睛】本题主要考查了函数的实际应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据自变量的值求算对应的函数值.
23.(1)一次函数表达式为;反比例函数表达式为
(2)或
【分析】本题主要考查了求一次函数解析式和反比例函数解析式,一次函数和反比例函数的交点问题;
(1)利用待定系数法求出一次函数和反比例函数解析式即可;
(2)根据图象得出当时,的解集即可.
【详解】(1)解:∵点和在反比例函数的图象上,
∴,
∴,.
∴反比例函数表达式为,点B的坐标为.
∵点和在一次函数的图象上,
∴,
解得,
∴一次函数表达式为;
(2)解:由图象可知,当或时反比例函数在一次函数的上面,
∴当时,的解集是或.
24.(1)见解析
(2)9
【分析】(1)连接,根据已知条件和圆的基本性质证明,得到即可.
(2)连接,根据圆周角定理得到,进一步证明,得到,可得结论.
【详解】(1)解:证明:如图,连接.
,
,
,
,
,
,
,
,
,
,
是半径,
是的切线.
(2)连接,如图.
是直径,
,
,
,
,
,
,
,
,
,
,
,
.
【点睛】本题考查圆周角定理,切线的判定与性质,相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.
25.(1)相切,见解析
(2)①见解析;②
【分析】(1)连接,根据,求得,根据等腰三角形的性质得到,推出,根据平行线的性质得到,于是得到是的切线;
(2)①连接,连接交于,根据垂径定理得到,,由圆周角定理得到,于是得到结论;
②根据勾股定理和矩形的性质得到, ,求得,根据梯形和扇形的面积公式即可得到结论.
【详解】(1)解:直线与相切,
理由:连接,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵是的半径,
∴是的切线;
(2)①证明:如图,连接,与相交于点F,
∵,
∴,,
∴AB是的直径,
∴,
∴,
∴四边形是矩形,
②解:∵,
∴,
在中,,
∴,
∴,
∴,
∴,
∴,
,
∴图中阴影部分的面积.
【点睛】本题考查了切线的判定与性质,矩形的判定,勾股定理,垂径定理,不规则图形的面积,扇形的面积的计算,正确的作出辅助线是解题的关键.
26.(1)见解析;
(2)出水口距地面的高度为2.44m,水达到最高点时与池中心的水平距离约为1.20m;
(3)出水口至少需要降低0.52m.
【分析】(1)根据表格中的数据,描点,连线画出图象;
(2)设y=ax +bx+2.44,将点(1,3.49),(2,3.04)代入求出解析式,然后求出对称轴即可;
(3)根据水柱落地点与池中心的距离不超过3.2m,得出a,b不变,只有c改变,将x=3.2代入求解即可.
【详解】(1)如图所示:
(2)由图象可得:当x=0时,y=2.44,
∴c=2.44,设y=ax +bx+2.44,
将点(1,3.49),(2,3.04)代入得:,解得:,
∴y=-0.75x +1.8x+2.44,
∴抛物线的对称轴为:,
∴y=-0.75×1.2 +1.8×1.2+2.44=3.52,
∴出水口距地面的高度为2.44m,水达到最高点时与池中心的水平距离约为1.20m;
(3)为了使水柱落地点与池中心的距离不超过3.2m,此时y=ax +bx+c中,a,b不变,只有c改变,
∴y=-0.75×3.2 +1.8×3.2+c,解得c=1.92,2.44-1.92=0.52(m),
∴出水口至少需要降低0.52m.
【点睛】本题考查了二次函数在实际生活中的运用,解题的关键是数形结合并熟练掌握待定系数法.
27.(1),画图见解析
(2)①;②
【分析】本题考查了二次函数的应用;
(1)待定系数法求解析式,通过描点法画出函数图象;
(2)①根据表格数据可得当时,,即可求解;
②根据题意,令,解方程,即可求解.
【详解】(1)解:设,把、、代入得,
,
解得,
,对称轴为直线,
在下面的平面直角坐标系中,画出所确定的函数图象;
(2)①当时,,
∴桥墩露出水面的高度为米,
②令,则,解得(舍去)或.
故答案为:,.
28.(1);
(2)每袋的销售价应定为25元,每日销售的最大利润是225元.
【分析】本题考查一次函数在销售问题的应用,二次函数在销售问题中的应用;
(1)设日销售量y(袋)与销售价x(元)的函数关系式为,代入数据,解二元一次方程组,即可求解;
(2)等量关系式:销售利润销售每袋土特产的利润每日的销售量,据此即可求解;
找出等量关系式,根据二次函数的性质求解是解题的关键.
【详解】(1)解:设日销售量y(袋)与销售价x(元)的函数关系式为,由题意得
得,
解得,
故日销售量y(袋)与销售价x(元)的函数关系式为:;
(2)解:设利润为w元,由题意得
,
当时,
w取得最大值,最大值为225,
故要使这种土特产每日销售的利润最大,每袋的销售价应定为25元,每日销售的最大利润是225元.
29.(1)距地面的高度为
(2)能实施有效救援,理由见解析
【分析】(1)过点作,过点B作,交于点F,交于点G,在中求出的长度,然后计算即可;
(2)当起重臂最长,转动张角最大时,同样求出的长度,与比较即可.
【详解】(1)解:如图,过点作,过点B作,交于点F,交于点G,
∵,
∴四边形是矩形,
∴,,
,
,
在中,
,
,
.
(2)解:能实施救援;
当起重臂最长,转动张角最大时,云梯消防车最高点B距地面最高,
即:米,,
,
,
.
,
能实施有效救援.
【点睛】本题考查了解直角三角形的应用,准确从图中提取数学模型是解题关键.
30.(1)m
(2)不是m,而是m
(3)云梯的顶端能到达高的墙头去救援被困人员
【分析】(1)本题考查解直角三角形,将梯子底部到墙的距离线段对应为一个直角边,梯子顶端到地的距离线段对应为另一个直角边,所以梯子顶端到地的距离为,所以梯子顶端到地为米;
(2)根据勾股定理求出,再与作差,求出的长度;
(3)先求出梯子能够到达墙面的最大高度,再与比较,即可求得.
【详解】(1)解:(1)在中,
∴.
(2)解:云梯的底部在水平方向滑动到的距离不是m.理由如下:
由(1)可知m,
∴.
在中,
∴,
∴.
(3)解:若云梯底端离墙的距离刚好为云梯长度的,
则能够到达墙面的最大高度为.
∵,
∴,
因此,云梯的顶端能到达高的墙头去救援被困人员.
31.(1)见解析
(2)
(3)见解析
【分析】本题主要考查了位似变换以及平移变换和解直角三角形,正确得出对应点位置是解题关键.
(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用正切的定义结合勾股定理得出答案;
(3)利用位似图形的性质得出对应点位置进而得出答案.
【详解】(1)解:如图,即为所求,
(2)解:如图,
由图知:,,,
∴.
故答案为:;
(3)解:如图,即为所求,
.
32.(1)①1,1,2;②或;;(2)
【分析】(1)①将代入求出k的值,得到,然后将代入求出,然后利用待定系数法将,代入求解即可;
②根据图象结合A,B两点的坐标即可求出不等式的解集;设直线与y轴交于点C,首先求出点C的坐标,得到,然后利用代数求解即可;
(2)首先根据题意求出,,过点M作轴于点M,过点A作交于点F,根据相似三角形的性质得到,,然后证明出,进而得到,然后代入求解即可.
【详解】(1)①根据题意得,
将代入得,,
解得,
∴,
将代入得,,
∴,
将,代入,
得,解得;
故答案为:1,1,2;
②∵,,
∴根据图象可得,不等式的解集或;
如图所示,设直线与y轴交于点C,
∵,,
∴,
∴当时,,
∴,
∴,
∴;
故答案为:或;;
(2)∵直线 与 x,y轴分别交于 A、B 两点,
∴当时,,
∴,
当时,,解得,
∴,
如图所示,过点M作轴于点M,过点A作交于点F,
∵,
∴,
∵,,
∴,
∵,
∴,,
∴,
∵轴,
∴,
∴,
∴,
∵,轴,
∴,
∴,
∵,,
∴,
∴,即,
∴,
∴,
∵点 M是双曲上一点,
∴,即,
解得或(舍去),
∴.
【点睛】本题是一次函数和反比例函数的交点问题,考查了待定系数法求函数的解析式,三角形的面积以及函数与不等式的关系,相似三角形的性质和判定等知识,数形结合是解题的关键.相似三角形的性质:相似三角形对应边成比例,对应角相等.相似三角形的判定方法:①两组角对应相等的两个三角形相似;②三边对应成比例的两个三角形相似;③两边对应成比例且夹角相等的两个三角形相似.
33.(1)见解析
(2)
【分析】(1)连接、,根据切线的性质得到,根据平行线的性质、等腰三角形的性质得到,根据圆周角定理、圆心角、弧、弦之间的关系定理证明结论;
(2)根据勾股定理求出,证明,根据相似三角形的性质列出比例式,代入计算得到答案.
【详解】(1)解:证明:
连接、,
是的切线,
,
,
,
,
,
,
,
由圆周角定理得,,,
,
;
(2)
由(1)可知,,
是的直径,
,
,
,,
,
,即,
解得,.
【点睛】本题考查的是切线的性质、相似三角形的判定和性质、圆周角定理,掌握圆的切线垂直于经过切点的半径是解题的关键.
34.(1)作图见解析
(2)
(3)或或,作图见解析
【分析】(1)先列表、然后描点、再连线即可得出函数图象;
(2)作出一次函数的函数图象,然后根据函数图象得出方程:的解即可;
(3)先列表、然后描点、再连线即可得出函数图象;方程可以变为,作出函数的函数图象,最后找出两个函数图象的交点,即可得出的解.
【详解】(1)解:列表:
x … 0 5 10 …
… 14 9 4 9 14 …
描点,连线,如图所示:
(2)解:如图,一次函数与函数的交点的横坐标为,
∴方程的解为,
故答案为:.
(3)解:列表:
x … 0 1 2 3 …
… 7 4 3 4 3 4 7 …
描点,连线:
方程可以变为,
如图,函数的图象与函数的图象交点的横坐标为:,,,
∴方程的解为或或,
即方程的解为或或.
【点睛】本题主要考查了用描点法作函数图象,根据函数图象求方程的解,解题的关键是熟练掌握函数图象的作图方法,数形结合.
35.探究检测距离为5米时,视力值1.2所对应行的“”形图边长为,视力值1.2所对应行的“”形图边长为;
探究;
探究3:检测距离为时,视力值1.2所对应行的“”形图边长为.
【分析】探究1:由图象中的点的坐标规律得到与成反比例关系,由待定系数法可得,将 代入得:;
探究2:由,知在自变量的取值范围内,随着的增大而减小,故当时,,即可得;
探究3:由素材可知,当某人的视力确定时,其分辨视角也是确定的,可得,即可解得答案.
【详解】探究
由图象中的点的坐标规律得到与成反比例关系,
设,将其中一点代入得:,
解得:,
,将其余各点一一代入验证,都符合关系式;
将 代入得:;
答:检测距离为5米时,视力值1.2所对应行的“”形图边长为,视力值1.2所对应行的“”形图边长为;
探究
,
在自变量的取值范围内,随着的增大而减小,
当时,,
,
;
探究3:由素材可知,当某人的视力确定时,其分辨视角也是确定的,由相似三角形性质可得,
由探究1知,
,
解得,
答:检测距离为时,视力值1.2所对应行的“”形图边长为.
【点睛】本题考查反比例函数的综合应用,涉及待定系数法,函数图象上点坐标的特征,相似三角形的性质等知识,解题的关键是读懂题意,能将生活中的问题转化为数学问题加以解决.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024年九年级开学数学巩固2
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.(2023上·广东深圳·九年级深圳外国语学校校考阶段练习)已知的半径为,,则点和的位置关系是( )
A.点在圆内 B.点在圆上 C.点在圆外 D.无法判断
2.(2023上·广东深圳·九年级校考阶段练习)如图,是的外接圆,,若的半径为6,则弦的长为( )
A.6 B. C. D.
3.(2023上·广东深圳·九年级校考阶段练习)如图,在中,,劣弧的度数是( )
A. B. C. D.
4.(2022上·广东深圳·八年级深圳市高级中学校考期中)在同一直角坐标系中,二次函数与一次函数的图象关系可能是( )
A. B. C. D.
5.(2023上·广东深圳·九年级校考期中)在同一平面直角坐标系中,函数与的大致图象可能是( )
A.B.C. D.
6.(2022上·广东深圳·九年级统考期末)若点在反比例函数的图象上,则的大小关系是( )
A. B. C. D.
7.(2021上·广东深圳·九年级校考期中)一次函数和反比例函数的图象在同一坐标系中可能为( )
A. B. C. D.
8.(2020上·广东深圳·九年级统考期末)二次函数与一次函数,它们在同一直角坐标系中的图象大致是( )
A. B. C. D.
9.(2023深圳·九年级校联考期中)抛物线的对称轴为直线,与x轴的一个交点坐标为,其部分图象如图所示,下列结论:①;②方程的两个根是,;③;④对于方程,有两个不相等的实数根,正确的有( )
①② B.①②④ C.③④ D.①②③④
10.(2023·广东深圳·深圳市桂园中学校考模拟预测)如图,二次函数的图象开口向下,且经过第三象限的点P.若点P的横坐标为,则一次函数的图象大致是( )
A. B. C. D.
11.(2021上·广东深圳·九年级校考期中)如图,已知:是斜边上的高线,是斜边上的高线,如果, ,那么等于( )
A.2 B.4.5 C.8 D.12.5
12.(2023上·广东深圳·九年级深圳市桂园中学校考阶段练习)点在函数图像上,下列说法中错误的是( )
A.它的图象分布在二、四象限 B.当时,的值随的增大而增大
C.当时,的值随的增大而减小 D.它的图象过点
评卷人得分
二、填空题
13.(2020·广东深圳·九年级校考阶段练习)如图,四边形内接于,是的直径,过C点的切线与的延长线交于P点.若,则的度数为 .
14.(2023上·广东深圳·九年级红岭中学校考阶段练习)若点,,在二次函数的图象上,则,,的大小关系是 .
15.(2023·广东深圳·深圳市桂园中学校考模拟预测)如图,某高速公路建设中需要测量某条江的宽度,飞机上的测量人员在C处测得A,B两点的俯角分别为和.若飞机离地面的高度为1600米,且点H,A,B在同一水平直线上,则这条江的宽度为 米(结果保留根号).
16.(2023上·广东深圳·九年级深圳市宝安第一外国语学校校联考阶段练习)如图,点是反比例函数图象上的一点,过点作轴于点,的面积为3,则的值为 .
17.(2023上·广东深圳·九年级深圳中学校考期末)如图,在平面直角坐标系中,矩形的边在x轴的正半轴上,边在y轴的正半轴上,反比例函数的图象与交于点D,与交于点F,与交于点G,当点G是的中点时,连接,若的面积为9,则k=
18.(2024上·广东深圳·九年级统考期末)如图,在矩形中,,,是上的一个动点(不与,重合),过点的反比例函数的图象与边交于点,若时,则 .
评卷人得分
三、解答题
19.(2023上·广东深圳·九年级红岭中学校考阶段练习)解方程:
(1);
(2).
(3)计算:.
(2023上·广东深圳·九年级校考阶段练习)
(1)解方程:.
(2)计算:.
(2022上·广东深圳·九年级深圳实验学校中学部校考阶段练习)
(1)计算:;
(2)解方程:.
22.(2022上·深圳·八年级深圳市高级中学校考期中)某市粮库要把晾晒场上的600吨大米入库封存.
(1)求入库所需的时间t(单位:天)与入库速度v(单位:吨/天)的函数关系式;
(2)粮库有职工 40 名,每人每天最多可将吨大米入库,预计将全部大米入库最快可在多少天内完成?
(3)粮库的职工连续工作了 25 天后,上级主管部门决定临时把剩下的大米全部入库,以便尽早调出出售,则至少需要增加多少名人员帮忙才能完成任务?
23.(2023上·广东深圳·九年级深圳市南山区华侨城中学校考阶段练习)如图,在平面直角坐标系中,已知反比例函数与一次函数的图象相交于点和.
(1)分别求反比例函数和一次函数的表达式;
(2)请直接写出当时,的解集.
24.(2022下·广东深圳·九年级校考周测)如图,在中,点是边上一点,以为直径的半圆经过点,点是弦上一点,过点作,垂足为,交的延长线于点,且.
(1)求证:直线与半圆相切;
(2)若已知,求的值.
25.(2023上·广东深圳·九年级校考阶段练习)如图,是的直径,E,C是上两点,且,连接,.过点C作交的延长线于点D.
(1)判定直线与的位置关系,并说明理由;
(2)连接和交于点F,若,,
①求证:四边形是矩形;
②求图中阴影部分的面积.
26.(2023·广东深圳·模拟预测)要修建一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,记喷出的水与池中心的水平距离为x m,距地面的高度为y m.测量得到如下数值:
x/m 0 0.5 1 1.5 2 2.5 3 3.37
y/m 2.44 3.15 3.49 3.45 3.04 2.25 1.09 0
小腾根据学习函数的经验,发现y是x的函数,并对y随x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)在平面直角坐标系xOy中,描出表中各组数值所对应的点,并画出函数的图象;
(2)结合函数图象,出水口距地面的高度为_______m,水达到最高点时与池中心的水平距离约为_______m(结果保留小数点后两位);
(3)为了使水柱落地点与池中心的距离不超过3.2m,如果只调整水管的高度,其他条件不变,结合函数图象,估计出水口至少需要_______(填“升高”或“降低”)_______m(结果保留小数点后两位).
27.(2023上·广东深圳·九年级深圳外国语学校校联考阶段练习)某公园内人工湖上有一座拱桥(横截面如图所示),跨度为米.在距点水平距离为米的地点,拱桥距离水面的高度为米.小红根据学习函数的经验,对和之间的关系进行了探究.
(1)经过测量,得出了和的几组对应值,如表.
米
米
请求出拱桥距离水面的高度与之间的函数关系式,画出确定的函数的图象;
(2)结合表格数据和函数图象,解决问题:
①桥墩露出水面的高度为 米;
②公园欲开设游船项目,现有长为米,宽为米,露出水面高度为米的游船.为安全起见,公园要在水面上的,两处设置警戒线,并且,要求游船能从,两点之间安全通过,则处距桥墩的距离至少为 米.(精确到米)
28.(2023上·广东深圳·九年级校考阶段练习)随着国家乡村振兴政策的推进,凤凰村农副产品越来越丰富,为增加该村村民收入,计划定价销售某土特产,他们把该土特产(每袋成本10元)进行4天试销售,日销量y(袋)和每袋售价x(元)记录如下:
时间 第一天 第二天 第三天 第四天
x/元 15 20 25 30
y/袋 25 20 15 10
若试销售和正常销售期间,日销量y与每袋售价x的一次函数关系相同,解决下列问题:
(1)求日销量y关于每袋售价x的函数关系式;
(2)请你帮村民设计,每袋售价定为多少元,才能使这种土特产每日销售的利润最大?并求出最大利润.(利润=销售额-成本)
29.(2023上·广东深圳·九年级深圳市桂园中学校考阶段练习)消防车是救援火灾的重要装备.图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂可伸缩,伸缩范围为,且起重臂可绕点A在一定范围内转动,张角为,张角范围为,转动点A距离地面的高度为(参考数据:)
(1)当起重臂长度为,张角为时,求云梯消防车最高点B距地面的高度;(结果保留根号)
(2)某栋楼高,若该楼中有居民家突发险情,请问该消防车能否实施有效救援?请说明理由.
30.(2023上·广东深圳·八年级深圳市海湾中学校考期中)综合与实践
【问题情境】某消防队在一次应急演练中,消防员架起一架长的云梯,如图,云梯斜靠在一面墙上,这时云梯底端距墙脚的距离,.
(1)【独立思考】这架云梯顶端距地面的距离有多高?
(2)【深入探究】消防员接到命令,按要求将云梯从顶端下滑到位置上(云梯长度不改变),,那么它的底部在水平方向滑动到的距离也是吗?若是,请说明理由;若不是,请求出的长度.
(3)【问题解决】在演练中,高的墙头有求救声,消防员需调整云梯去救援被困人员.经验表明,云梯靠墙摆放时,如果云梯底端离墙的距离不小于云梯长度的,则云梯和消防员相对安全.在相对安全的前提下,云梯的顶端能否到达高的墙头去救援被困人员?
31.(2021上·广东深圳·九年级校考期中)如图,中,,,.
(1)请画出将向右平移8个单位长度后的;
(2) ;
(3)以O为位似中心,将缩小为原来的,得到,请在y轴右侧画出并直接写出的坐标.
32.(2023上·广东深圳·九年级校考期中)(1)如图1,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点和.
①直接写出____,____,____;
②请直接写出不等式的解集____;连接、,则_______.
(2)如图 2,直线 与 x,y轴分别交于 A、B 两点,点 M是双曲上一点,分别连接、.在双曲线上是否存在点 M,使得以为斜边的与相似?若存在,请求出点 M 的坐标; 若不存在,请说明理由.
33.(2023·广东深圳·南山实验教育集团南海中学校考三模)如图,为的直径,为上一点,与过点的切线互相垂直,垂足为点,交于点,连接,.
(1)求证:;
(2)若,,求的长.
34.(2023·广东深圳·校考模拟预测)请结合图像完成下列问题:
(1)请在图中画出函数:的图像;
(2)结合图像直接写出方程:的解为:_______;
(3)在图中画出函数的图像,并结合图像直接写出方程:的解为: .
35.(2023上·广东深圳·九年级校考阶段练习)视力表中蕴含着很多数学知识,如:每个“E”形图都是正方形结构,同一行的“E”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表.
素材1 国际通用的视力表以5米为检测距离,任选视力表中7个视力值n,测得对应行的“E”形图边长b(mm),在平面直角坐标系中描点如图1.
探究1 检测距离为5米时,归纳n与b的关系式,并求视力值1.2所对应行的“E”形图边长.
素材2 图2为视网膜成像示意图,在检测视力时,眼睛能看清最小“E”形图所成的角叫做分辨视角,视力值与分辨视角(分)的对应关系近似满足.
探究2 当时,属于正常视力,根据函数增减性写出对应的分辨视角的范围.
素材3 如图3,当确定时,在A处用边长为的I号“E”测得的视力与在B处用边长为的Ⅱ号“E”测得的视力相同.
探究3 若检测距离为3米,求视力值1.2所对应行的“E”形图边长.
参考答案:
1.C
【分析】本题主要考查了点与圆的位置关系,根据“若点与圆心的距离d,圆的半径为,则当时,点在圆外;当时,点在圆上;当时,点在圆内”,即可求解.
【详解】解:∵的半径为,,
∴的半径,
∴点和的位置关系是点在圆外.
故选:C
2.B
【分析】此题考查了圆周角定理,勾股定理,首先根据圆周角定理得到,然后利用勾股定理求解即可.解题的关键是熟练掌握圆周角定理(同弧所对的圆心角是圆周角的两倍)和勾股定理(若直角三角形的两条直角边为a和b,斜边为c,则).
【详解】∵
∴
∵的半径为6,
∴
∴.
故选:B.
3.D
【分析】本题考查了弧所对的度数求解,只需求出弧所对的圆心角度数即可.连接,根据结合即可求出.
【详解】解:连接,如图所示:
则
∵,
∴
∴
故劣弧的度数是
故选:D
4.C
【分析】根据题意得:二次函数的图象与x轴的对称点为,再结合二次函数与一次函数的图象,确定a,b的取值范围,即可求解.
【详解】解:根据题意得:二次函数的图象与x轴的对称点为,
A、观察一次函数的图象得,由二次函数的图象得,则,矛盾,故本选项不符合题意;
B、观察一次函数的图象得,由二次函数的图象得,矛盾,故本选项不符合题意;
C、观察一次函数的图象得,由二次函数的图象得,则,相一致,故本选项符合题意;
D、观察一次函数的图象得,由二次函数的图象得,矛盾,故本选项不符合题意;
故选:C
5.D
【分析】本题主要考查了反比例函数的图象和一次函数的图象,熟悉两函数中k的符号对函数图象的影响是解题的关键.
【详解】解:①当时,过一、三、四象限;位于一、三象限;
②当时,过一、二、四象象限;位于二、四象限.
观察图形可知,只有D选项符合题意.
故选D.
6.C
【分析】本题主要考查了比较反比例函数值的大小,根据解析式判断出反比例函数图象经过第二、四象限,且在每个象限内y随x增大而增大是解题的关键.
【详解】解:∵反比例函数解析式为,,
∴反比例函数图象经过第二、四象限,且在每个象限内y随x增大而增大,
∵点在反比例函数的图象上,,
∴,
故选C.
7.C
【分析】此题考查反比例函数和一次函数的图象共存问题;结合图象分别分析一次函数与反比例函数中,的符号,得出一致的符合题意,得出矛盾的不符合题意,从而可得答案.
【详解】解:A选项:由反比例函数的性质知k、b同号,由一次函数图象得,,得k、b异号.两者不一致,故A不符合题意;
B选项:由反比例函数的性质知k、b同号,由一次函数图象得,,两者不一致,故B不符合题意;
C选项:由反比例函数的性质知k、b异号,由一次函数图象得,,k、b异号,两者一致,故C符合题意;
D选项:由反比例函数的性质知k、b异号,由一次函数图象得,,k、b同号,两者不一致.故D不符合题意;
故选C
8.A
【分析】利用二次函数和一次函数图象的性质“二次函数和一次函数的常数项是图象与y轴交点的纵坐标;一次函数的一次项系数大于0,图象经过一、三象限;小于0,经过二、四象限;二次函数的二次项系数大于0,图象开口向上;二次项系数小于0,图象开口向下.”逐项判断即可.
【详解】A.图象中二次函数,一次函数,故A符合题意.
B.图象中二次函数,一次函数,故B不符合题意.
C.图象中二次函数,一次函数,故C不符合题意.
D.图象中二次函数,一次函数,故D不符合题意.
故选:A.
【点睛】本题考查二次函数及一次函数的图象的性质.熟练掌握二次函数和一次函数的图象的性质是解答本题的关键.
9.B
【分析】本题考查了二次函数、一元二次方程、二元一次方程组的知识;根据题意,得时,;结合二次函数对称轴的性质,根据函数图象以及对称轴,即可得到抛物线与轴的交点,再根据二次函数图像的性质分析,即可完成求解.
【详解】根据题意,时,
∵抛物线的对称轴为直线,
∴.
∵抛物线与轴的一个交点坐标为
∴另一个交点为,
∵抛物线与轴有2个交点,
∴
∴成立,
∴①正确;
∴方程的两个根是,,
∴②正确;
∵图象与x轴交于点,
∴
∴③不正确;
∵对于方程,有两个不相等的实数根,
观察函数图象,可得与 有2个交点,
∴④正确;
∴结论正确的是①②④
故选:B.
10.C
【分析】根据二次函数的图象可以判断a、b的正负情况,从而可以得到一次函数经过哪几个象限即可.
【详解】解:由二次函数的图象可知,,
对称轴在y轴左侧,左同右异,,
∴,一次函数与y轴正半轴有交点,
故选:C.
【点睛】本题考查二次函数的性质、一次函数的性质,解答本题的关键是明确题意,利用函数的思想解答.
11.D
【分析】本题考查了解直角三角形的应用,相似三角形的判定与性质,设,先证明,根据等角的正切值相等可得,再证明,根据相似三角形面积比等于相似比的平方即可得出结论.
【详解】解:∵,
∴
设,,
∵,,
∴,
∴,,
∴,
∴,
∴,
∴.
∵,
∴,
∵,
∴,
∴,
∵,
∴,
故选:D.
12.C
【分析】此题主要考查了反比例函数的图象性质,先把点代入,求得,根据反比例函数的性质:当,双曲线的两支分别位于第二、第四象限,在每一象限内随的增大而增大,图象既是轴对称图形又是中心对称图形进行判断即可.
【详解】解:把点代入,得
,
解得:,
∴,
A、∵,∴的图象分布在二、四象限,原说法正确,故此选项不符合题意;
B、∵,∴当时,的值随的增大而增大,原说法正确,故此选项不符合题意;
C、∵,∴当时,的值随的增大而增大,原说法错误,故此选项符合题意;
D、∵把代入,得,∴它的图象过点,原说法正确,故此选项不符合题意;
故选:C.
13./115度
【分析】根据过C点的切线与的延长线交于P点,,连接点C和圆心O,可以求得和的度数,又根据圆内接四边形对角互补,可以求得的度数,本题得以解决.本题考查切线的性质、圆内接四边形对角互补,解题的关键是连接圆心和切点,构造直角三角形,求出四边形的一个角,找出所求问题需要的条件.
【详解】解:连接,如图所示,
由题意可得,,
,
,
,
∵四边形是圆内接四边形,
,
,
故答案为:.
14.
【分析】本题考查了二次函数的性质,根据图象上的点的横坐标距离对称轴的远近来判断纵坐标的大小,解题的关键是熟练掌握二次函数的增减性.
【详解】解:由题知,抛物线的开口向上,且对称轴是直线,
∴函数图象上的点,离对称轴越近,函数值越小,
∵,
∴,
故答案为:.
15.
【分析】由题意易得,然后根据米及三角函数可求解.
【详解】解:由题意可得:,
∵,
∴,
∵米
∴(米),
(米),
∴米.
故答案为:.
【点睛】本题主要考查解直角三角形,熟练掌握三角函数的定义是解题的关键.
16.
【分析】本题考查了反比例函数的性质、反比例函数值的几何意义,由题意得,再根据反比例函数的图象在第二象限,即可得出,熟练掌握反比例函数值的几何意义是解此题的关键.
【详解】解:由题意得:,
,
反比例函数的图象在第二象限,
,
,
故答案为:.
17.12
【分析】连接,根据题意以及反比例函数系数k的几何意义得到,从而表示出矩形的面积,设设,则,最后列出方程求解即可.
【详解】解∶连接OD,
∵矩形的边在x轴的正半轴上,边在y轴的正半轴上,矩形交反比例函数于点D、F,
∴,
∵点G是的中点,的面积为9,
∴,
∴,
∴,
∴矩形的面积为,
设,则,
∴,
解得,
故答案为∶12.
【点睛】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,矩形的性质,三角形的面积,能用含k的式子表示出矩形的面积以及点B的坐标是解题的关键.
18.80
【分析】本题考查了反比例函数的几何意义的应用,三角形面积的同底问题的应用.连接,利用同底面积比等于高之比,得到点坐标,再利用反比例函数的关系式的求法计算即可.
【详解】解:连接,
由题意得:,
,
,
,,
,
,
,
.
故答案为:80.
19.(1),
(2),
(3)
【分析】此题考查了解一元二次方程,特殊角的三角函数值.
(1)利用配方法解方程即可;
(2)利用因式分解法解方程即可;
(3)根据有理数的乘方、特殊角的三角函数值化简,然后进行二次根式的加减运算即可.
【详解】(1)解:,
移项,得,
除以2,得,
配方,得,
即,
开方得,
解得:,;
(2)解:,
整理得:,
,
或,
解得:,;
(3)解:原式
.
20.(1),;(2)0
【分析】本题考查解一元二次方程,特殊角三角函数的混合运算:
(1)利用配方法或公式法求解;
(2)将特殊角三角函数值代入计算即可.
【详解】解:(1),
,
,
,
,
,
解得,.
(2)
21.(1);(2),
【分析】本题主要考查负指数幂,特殊角的三角函数值的计算,绝对值的性质,因式分解求一元二次方程,掌握实数的计算方法,因式分解法求一元二次方程的解是解题的关键.
(1)先算负指数幂,特殊角的三角函数值,绝对值的化简,再根据实数的混合运算法则即可求解;
(2)移项,提取公因式进行因数分解即可求解.
【详解】解:(1)
;
(2)
移项得,
提取公因式得,,整理得,
∴或,
∴,.
22.(1)
(2)30
(3)160人
【分析】(1)根据工作时间工作总量工作效率可得函数关系式;
(2)直接把代入解析式求解即可;
(3)根据题意求出剩余的玉米一天内全部入库需职工人数为200人,所以需增加的人数即可求出.
【详解】(1)解:根据关系式:工作时间工作总量工作效率可得:
入库所需的时间 t 与入库速度 v 的函数关系式为;
(2)根据题意得:,
∴预计将全部大米入库最快可在30天内完成;
(3)粮库的职工连续工作了25天的入库量为,
由题可知:剩下的粮食需要再一天内完成入库,
则所需人数为 (人),
(人).
【点睛】本题主要考查了函数的实际应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据自变量的值求算对应的函数值.
23.(1)一次函数表达式为;反比例函数表达式为
(2)或
【分析】本题主要考查了求一次函数解析式和反比例函数解析式,一次函数和反比例函数的交点问题;
(1)利用待定系数法求出一次函数和反比例函数解析式即可;
(2)根据图象得出当时,的解集即可.
【详解】(1)解:∵点和在反比例函数的图象上,
∴,
∴,.
∴反比例函数表达式为,点B的坐标为.
∵点和在一次函数的图象上,
∴,
解得,
∴一次函数表达式为;
(2)解:由图象可知,当或时反比例函数在一次函数的上面,
∴当时,的解集是或.
24.(1)见解析
(2)9
【分析】(1)连接,根据已知条件和圆的基本性质证明,得到即可.
(2)连接,根据圆周角定理得到,进一步证明,得到,可得结论.
【详解】(1)解:证明:如图,连接.
,
,
,
,
,
,
,
,
,
,
是半径,
是的切线.
(2)连接,如图.
是直径,
,
,
,
,
,
,
,
,
,
,
,
.
【点睛】本题考查圆周角定理,切线的判定与性质,相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.
25.(1)相切,见解析
(2)①见解析;②
【分析】(1)连接,根据,求得,根据等腰三角形的性质得到,推出,根据平行线的性质得到,于是得到是的切线;
(2)①连接,连接交于,根据垂径定理得到,,由圆周角定理得到,于是得到结论;
②根据勾股定理和矩形的性质得到, ,求得,根据梯形和扇形的面积公式即可得到结论.
【详解】(1)解:直线与相切,
理由:连接,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵是的半径,
∴是的切线;
(2)①证明:如图,连接,与相交于点F,
∵,
∴,,
∴AB是的直径,
∴,
∴,
∴四边形是矩形,
②解:∵,
∴,
在中,,
∴,
∴,
∴,
∴,
∴,
,
∴图中阴影部分的面积.
【点睛】本题考查了切线的判定与性质,矩形的判定,勾股定理,垂径定理,不规则图形的面积,扇形的面积的计算,正确的作出辅助线是解题的关键.
26.(1)见解析;
(2)出水口距地面的高度为2.44m,水达到最高点时与池中心的水平距离约为1.20m;
(3)出水口至少需要降低0.52m.
【分析】(1)根据表格中的数据,描点,连线画出图象;
(2)设y=ax +bx+2.44,将点(1,3.49),(2,3.04)代入求出解析式,然后求出对称轴即可;
(3)根据水柱落地点与池中心的距离不超过3.2m,得出a,b不变,只有c改变,将x=3.2代入求解即可.
【详解】(1)如图所示:
(2)由图象可得:当x=0时,y=2.44,
∴c=2.44,设y=ax +bx+2.44,
将点(1,3.49),(2,3.04)代入得:,解得:,
∴y=-0.75x +1.8x+2.44,
∴抛物线的对称轴为:,
∴y=-0.75×1.2 +1.8×1.2+2.44=3.52,
∴出水口距地面的高度为2.44m,水达到最高点时与池中心的水平距离约为1.20m;
(3)为了使水柱落地点与池中心的距离不超过3.2m,此时y=ax +bx+c中,a,b不变,只有c改变,
∴y=-0.75×3.2 +1.8×3.2+c,解得c=1.92,2.44-1.92=0.52(m),
∴出水口至少需要降低0.52m.
【点睛】本题考查了二次函数在实际生活中的运用,解题的关键是数形结合并熟练掌握待定系数法.
27.(1),画图见解析
(2)①;②
【分析】本题考查了二次函数的应用;
(1)待定系数法求解析式,通过描点法画出函数图象;
(2)①根据表格数据可得当时,,即可求解;
②根据题意,令,解方程,即可求解.
【详解】(1)解:设,把、、代入得,
,
解得,
,对称轴为直线,
在下面的平面直角坐标系中,画出所确定的函数图象;
(2)①当时,,
∴桥墩露出水面的高度为米,
②令,则,解得(舍去)或.
故答案为:,.
28.(1);
(2)每袋的销售价应定为25元,每日销售的最大利润是225元.
【分析】本题考查一次函数在销售问题的应用,二次函数在销售问题中的应用;
(1)设日销售量y(袋)与销售价x(元)的函数关系式为,代入数据,解二元一次方程组,即可求解;
(2)等量关系式:销售利润销售每袋土特产的利润每日的销售量,据此即可求解;
找出等量关系式,根据二次函数的性质求解是解题的关键.
【详解】(1)解:设日销售量y(袋)与销售价x(元)的函数关系式为,由题意得
得,
解得,
故日销售量y(袋)与销售价x(元)的函数关系式为:;
(2)解:设利润为w元,由题意得
,
当时,
w取得最大值,最大值为225,
故要使这种土特产每日销售的利润最大,每袋的销售价应定为25元,每日销售的最大利润是225元.
29.(1)距地面的高度为
(2)能实施有效救援,理由见解析
【分析】(1)过点作,过点B作,交于点F,交于点G,在中求出的长度,然后计算即可;
(2)当起重臂最长,转动张角最大时,同样求出的长度,与比较即可.
【详解】(1)解:如图,过点作,过点B作,交于点F,交于点G,
∵,
∴四边形是矩形,
∴,,
,
,
在中,
,
,
.
(2)解:能实施救援;
当起重臂最长,转动张角最大时,云梯消防车最高点B距地面最高,
即:米,,
,
,
.
,
能实施有效救援.
【点睛】本题考查了解直角三角形的应用,准确从图中提取数学模型是解题关键.
30.(1)m
(2)不是m,而是m
(3)云梯的顶端能到达高的墙头去救援被困人员
【分析】(1)本题考查解直角三角形,将梯子底部到墙的距离线段对应为一个直角边,梯子顶端到地的距离线段对应为另一个直角边,所以梯子顶端到地的距离为,所以梯子顶端到地为米;
(2)根据勾股定理求出,再与作差,求出的长度;
(3)先求出梯子能够到达墙面的最大高度,再与比较,即可求得.
【详解】(1)解:(1)在中,
∴.
(2)解:云梯的底部在水平方向滑动到的距离不是m.理由如下:
由(1)可知m,
∴.
在中,
∴,
∴.
(3)解:若云梯底端离墙的距离刚好为云梯长度的,
则能够到达墙面的最大高度为.
∵,
∴,
因此,云梯的顶端能到达高的墙头去救援被困人员.
31.(1)见解析
(2)
(3)见解析
【分析】本题主要考查了位似变换以及平移变换和解直角三角形,正确得出对应点位置是解题关键.
(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用正切的定义结合勾股定理得出答案;
(3)利用位似图形的性质得出对应点位置进而得出答案.
【详解】(1)解:如图,即为所求,
(2)解:如图,
由图知:,,,
∴.
故答案为:;
(3)解:如图,即为所求,
.
32.(1)①1,1,2;②或;;(2)
【分析】(1)①将代入求出k的值,得到,然后将代入求出,然后利用待定系数法将,代入求解即可;
②根据图象结合A,B两点的坐标即可求出不等式的解集;设直线与y轴交于点C,首先求出点C的坐标,得到,然后利用代数求解即可;
(2)首先根据题意求出,,过点M作轴于点M,过点A作交于点F,根据相似三角形的性质得到,,然后证明出,进而得到,然后代入求解即可.
【详解】(1)①根据题意得,
将代入得,,
解得,
∴,
将代入得,,
∴,
将,代入,
得,解得;
故答案为:1,1,2;
②∵,,
∴根据图象可得,不等式的解集或;
如图所示,设直线与y轴交于点C,
∵,,
∴,
∴当时,,
∴,
∴,
∴;
故答案为:或;;
(2)∵直线 与 x,y轴分别交于 A、B 两点,
∴当时,,
∴,
当时,,解得,
∴,
如图所示,过点M作轴于点M,过点A作交于点F,
∵,
∴,
∵,,
∴,
∵,
∴,,
∴,
∵轴,
∴,
∴,
∴,
∵,轴,
∴,
∴,
∵,,
∴,
∴,即,
∴,
∴,
∵点 M是双曲上一点,
∴,即,
解得或(舍去),
∴.
【点睛】本题是一次函数和反比例函数的交点问题,考查了待定系数法求函数的解析式,三角形的面积以及函数与不等式的关系,相似三角形的性质和判定等知识,数形结合是解题的关键.相似三角形的性质:相似三角形对应边成比例,对应角相等.相似三角形的判定方法:①两组角对应相等的两个三角形相似;②三边对应成比例的两个三角形相似;③两边对应成比例且夹角相等的两个三角形相似.
33.(1)见解析
(2)
【分析】(1)连接、,根据切线的性质得到,根据平行线的性质、等腰三角形的性质得到,根据圆周角定理、圆心角、弧、弦之间的关系定理证明结论;
(2)根据勾股定理求出,证明,根据相似三角形的性质列出比例式,代入计算得到答案.
【详解】(1)解:证明:
连接、,
是的切线,
,
,
,
,
,
,
,
由圆周角定理得,,,
,
;
(2)
由(1)可知,,
是的直径,
,
,
,,
,
,即,
解得,.
【点睛】本题考查的是切线的性质、相似三角形的判定和性质、圆周角定理,掌握圆的切线垂直于经过切点的半径是解题的关键.
34.(1)作图见解析
(2)
(3)或或,作图见解析
【分析】(1)先列表、然后描点、再连线即可得出函数图象;
(2)作出一次函数的函数图象,然后根据函数图象得出方程:的解即可;
(3)先列表、然后描点、再连线即可得出函数图象;方程可以变为,作出函数的函数图象,最后找出两个函数图象的交点,即可得出的解.
【详解】(1)解:列表:
x … 0 5 10 …
… 14 9 4 9 14 …
描点,连线,如图所示:
(2)解:如图,一次函数与函数的交点的横坐标为,
∴方程的解为,
故答案为:.
(3)解:列表:
x … 0 1 2 3 …
… 7 4 3 4 3 4 7 …
描点,连线:
方程可以变为,
如图,函数的图象与函数的图象交点的横坐标为:,,,
∴方程的解为或或,
即方程的解为或或.
【点睛】本题主要考查了用描点法作函数图象,根据函数图象求方程的解,解题的关键是熟练掌握函数图象的作图方法,数形结合.
35.探究检测距离为5米时,视力值1.2所对应行的“”形图边长为,视力值1.2所对应行的“”形图边长为;
探究;
探究3:检测距离为时,视力值1.2所对应行的“”形图边长为.
【分析】探究1:由图象中的点的坐标规律得到与成反比例关系,由待定系数法可得,将 代入得:;
探究2:由,知在自变量的取值范围内,随着的增大而减小,故当时,,即可得;
探究3:由素材可知,当某人的视力确定时,其分辨视角也是确定的,可得,即可解得答案.
【详解】探究
由图象中的点的坐标规律得到与成反比例关系,
设,将其中一点代入得:,
解得:,
,将其余各点一一代入验证,都符合关系式;
将 代入得:;
答:检测距离为5米时,视力值1.2所对应行的“”形图边长为,视力值1.2所对应行的“”形图边长为;
探究
,
在自变量的取值范围内,随着的增大而减小,
当时,,
,
;
探究3:由素材可知,当某人的视力确定时,其分辨视角也是确定的,由相似三角形性质可得,
由探究1知,
,
解得,
答:检测距离为时,视力值1.2所对应行的“”形图边长为.
【点睛】本题考查反比例函数的综合应用,涉及待定系数法,函数图象上点坐标的特征,相似三角形的性质等知识,解题的关键是读懂题意,能将生活中的问题转化为数学问题加以解决.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
