五年级下册数学北师大版2.6 长方体(一)练习二课件(共26张PPT)
文档属性
| 名称 | 五年级下册数学北师大版2.6 长方体(一)练习二课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 16:24:18 | ||
图片预览




文档简介
(共26张PPT)
练习二
第二单元 长方体(一)
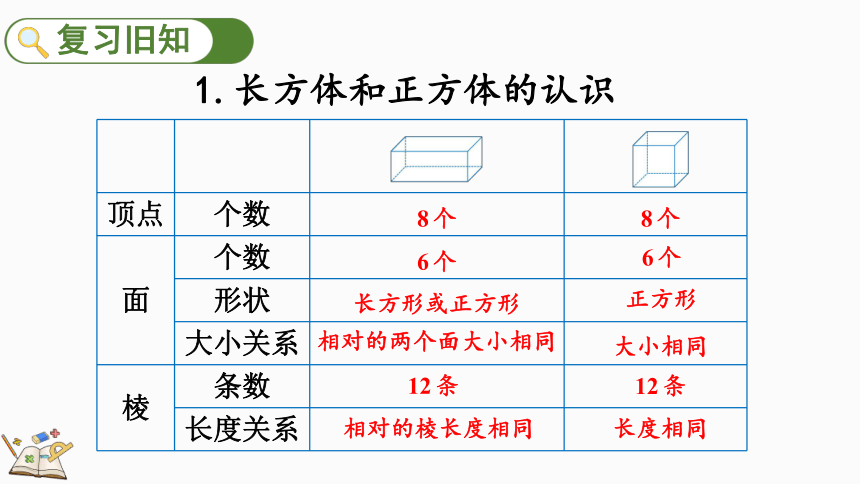
1.长方体和正方体的认识
顶点 个数
面 个数
形状
大小关系
棱 条数
长度关系
8个
8个
6个
6个
正方形
长方形或正方形
大小相同
相对的两个面大小相同
12条
12条
长度相同
相对的棱长度相同
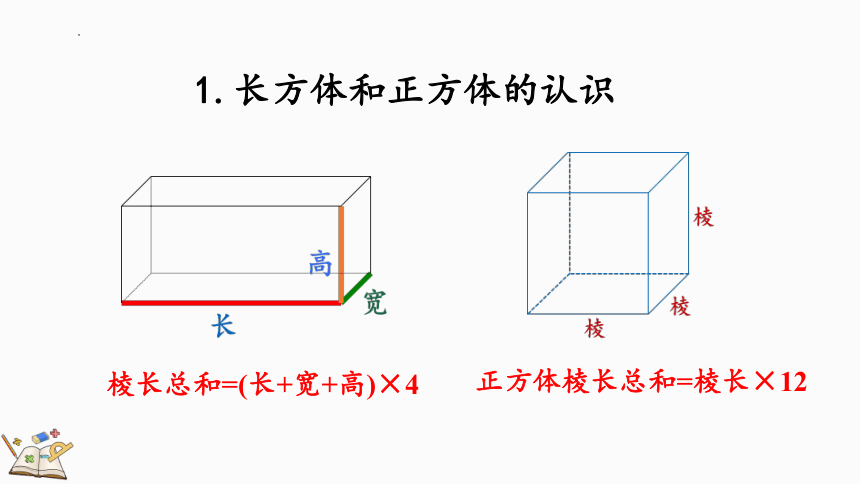
1.长方体和正方体的认识
正方体棱长总和=棱长×12
棱长总和=(长+宽+高)×4
正方体的展开图是由6个完全相同的正方形组成的组合图形,并且相对的面完全隔开。
长方体的展开图由6个长方形(特殊情况有两个正方形)组成,相对的面完全相同且隔开。
2.展开与折叠
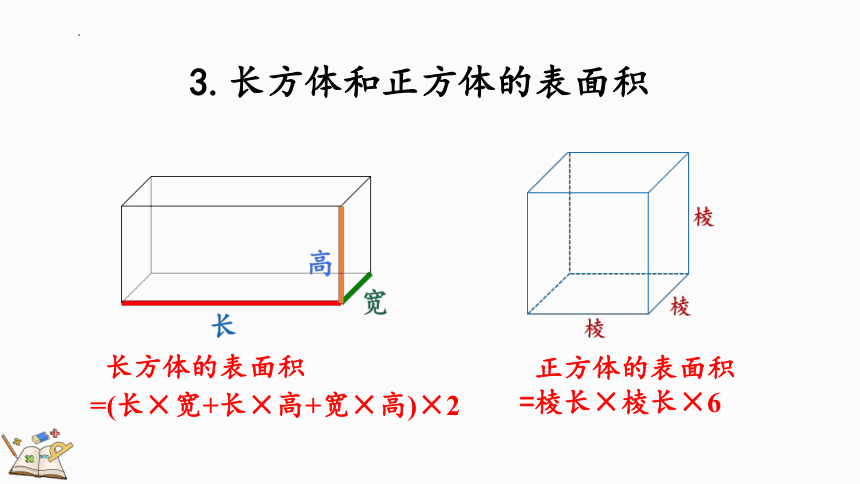
3.长方体和正方体的表面积
正方体的表面积
=棱长×棱长×6
长方体的表面积
=(长×宽+长×高+宽×高)×2
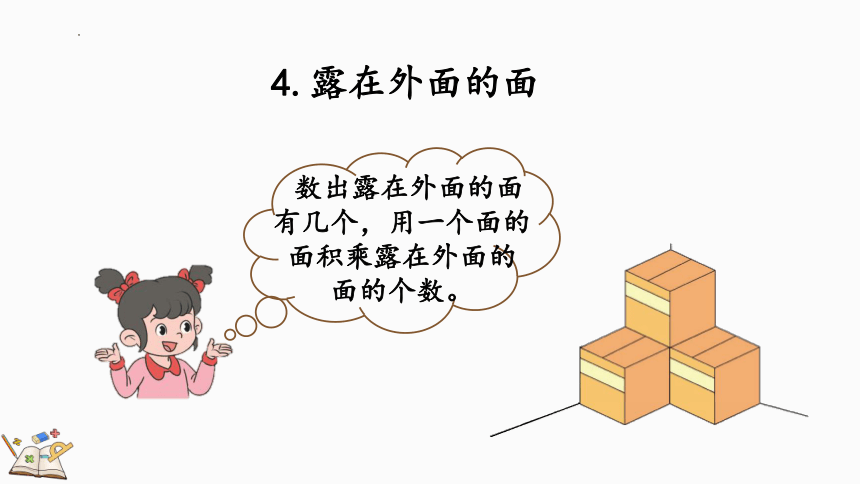
4.露在外面的面
数出露在外面的面有几个,用一个面的面积乘露在外面的
面的个数。
如图。(单位:cm)
1
选自教材第20~21页练习二
(1)图①和图②分别是什么图形?
答:图①是正方体,图②是长方体。
选自教材第20~21页练习二
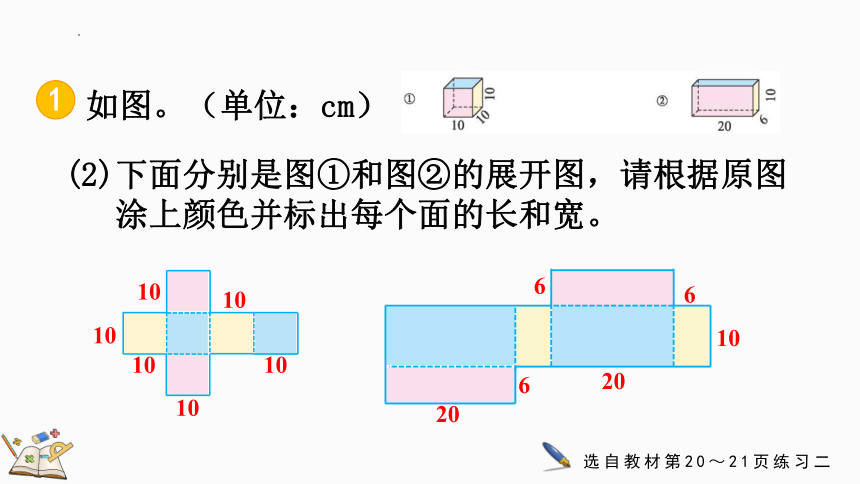
(2)下面分别是图①和图②的展开图,请根据原图
涂上颜色并标出每个面的长和宽。
如图。(单位:cm)
1
10
10
10
10
10
10
20
6
20
10
6
6
选自教材第20~21页练习二
(3)图①的棱长总和是多少?图②的表面积是多少?
如图。(单位:cm)
1
正方体的棱长总和
=棱长×12
10×12
=120 (cm)
长方体的表面积
=(长×宽+长×高+宽×高)×2
(20×6+20×10+10×6)×2
=380×2
=760 (cm )
下图中哪些是正方体的展开图?是的画“√”,不是的画“×”,可以利用附页2中的图2做一做。
2
选自教材第20~21页练习二
×
√
√
√
3
选自教材第20~21页练习二
淘气要把一个如下图所示的空包装箱的各面都贴上彩纸,至少需要多少平方厘米的彩纸 (单位:cm)
(40×25+40×40+40×25)×2=7200(平方厘米)
答:至少需要7200平方厘米的彩纸。
40
40
25
长方体的表面积
=(长×宽+长×高+宽×高)×2
选自教材第20~21页练习二
4
6个棱长都是20cm的正方体纸箱堆放在墙角处(如右图),露出多少个面?露在外面的面的面积是多少平方厘米?
方法一
一个一个地数
20×20×13=5200(平方厘米)
答:露出13个面,露在外面的面的面积是5200平方厘米。
选自教材第20~21页练习二
4
6个棱长都是20cm的正方体纸箱堆放在墙角处(如右图),露出多少个面?露在外面的面的面积是多少平方厘米?
从上、前、右三个角度数
方法二
20×20×13=5200(平方厘米)
答:露出13个面,露在外面的面的面积是5200平方厘米。
选自教材第20~21页练习二
5
将一个由5个棱长是10cm的正方体拼成的长方体拆开(如下图),5个正方体的表面积之和是多少?与长方体的表面积相等吗?与同伴交流。
求出一个小正方体的表面积×5
10×10×6×5=3000(平方厘米)
长方体的表面积:50×10×4+10×10×2=2200(平方厘米)
答:5个正方体的表面积之和是3000平方厘米,与长方体的表面积不相等。
方法一
选自教材第20~21页练习二
5
将一个由5个棱长是10cm的正方体拼成的长方体拆开(如下图),5个正方体的表面积之和是多少?与长方体的表面积相等吗?与同伴交流。
求出长方体的表面积+增加的面积
50×10×4+10×10×2+10×10×8=3000(平方厘米)
答:5个正方体的表面积之和是3000平方厘米。与长方体的表面积不相等。
方法二
选自教材第20~21页练习二
6
用同一种原材料做一个如右图的抽屉,至少需要多大面积的材料?(单位:dm)
(3.5×1.5+5×1.5)×2+3.5×5=43(平方分米)
答:至少需要43平方分米的材料。
这个长方体没有上面。
选自教材第20~21页练习二
7
如图,三种不同长度的小棒分别有12根、8根、4根,请你搭出3种不同的长方体或正方体,并填写下表。
序号 图形名称 长/cm 宽/cm 高/cm
选自教材第20~21页练习二
②
①
③
正方体
15
有两个面是正方形的长方体
10
10
8
长方体
15
10
8
15
15
8
一根绳子长10m,现要捆扎一种礼盒(如右图)。如果结头处要用掉绳子25cm,这根绳子最多可以捆扎几个这样的礼盒?(单位:cm)
选自教材第20~21页练习二
捆扎一个礼盒相当于:2个长,2个宽,4个高和1个结。
2×10+2×15+4×8+25=107(厘米)
10 m=1000 cm
1000÷107=9(个) ……37(厘米)
答:最多可以捆扎9个这样的礼盒。
1.做一个长2 m、宽1.5 m、高8 dm的长方体铁皮箱子,至少需要多少平方米铁皮?
注意统一单位。
8 dm=0.8 m
(2×1.5+2×0.8+1.5×0.8)×2
=5.8×2
=11.6(m )
答:至少需要11.6平方米铁皮。
2. 将两个一样的正方体木块拼成一个长方体木块,已知长方体木块的棱长总和是96 cm,原来两个正方体木块的棱长总和是多少厘米?
12×2=24 (条)
24-8=16 (条)
棱的条数:
答:原来两个正方体木块的棱长总和是144厘米。
96÷16=6 (cm)
12×6×2=144 (cm)
长方体和正方体都有8个顶点,6个面,12条棱
正方体是特殊的长方体
长方体的棱长总和=(长+宽+高)×4
正方体的棱长总和=棱长×12
这节课有什么收获呢?
长方体展开图由6个长方形(特殊情况下有2个正方形)组成,相对的面完全相同且隔开。
正方体由6个完全相同的正方形组成。
这节课有什么收获呢?
这节课有什么收获呢?
长方体或正方体6个面的面积之和,叫作它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长×棱长×6
堆放在墙角的正方体露在外面的面积的计算方法:
数出露在外面的面有几个,用一个面的面积乘露在外面的面的个数。
这节课有什么收获呢?
长方体和正方体的认识
长方体(一)
展开与折叠
露在外面的面
长方体和正方体的表面积
练习二
第二单元 长方体(一)
1.长方体和正方体的认识
顶点 个数
面 个数
形状
大小关系
棱 条数
长度关系
8个
8个
6个
6个
正方形
长方形或正方形
大小相同
相对的两个面大小相同
12条
12条
长度相同
相对的棱长度相同
1.长方体和正方体的认识
正方体棱长总和=棱长×12
棱长总和=(长+宽+高)×4
正方体的展开图是由6个完全相同的正方形组成的组合图形,并且相对的面完全隔开。
长方体的展开图由6个长方形(特殊情况有两个正方形)组成,相对的面完全相同且隔开。
2.展开与折叠
3.长方体和正方体的表面积
正方体的表面积
=棱长×棱长×6
长方体的表面积
=(长×宽+长×高+宽×高)×2
4.露在外面的面
数出露在外面的面有几个,用一个面的面积乘露在外面的
面的个数。
如图。(单位:cm)
1
选自教材第20~21页练习二
(1)图①和图②分别是什么图形?
答:图①是正方体,图②是长方体。
选自教材第20~21页练习二
(2)下面分别是图①和图②的展开图,请根据原图
涂上颜色并标出每个面的长和宽。
如图。(单位:cm)
1
10
10
10
10
10
10
20
6
20
10
6
6
选自教材第20~21页练习二
(3)图①的棱长总和是多少?图②的表面积是多少?
如图。(单位:cm)
1
正方体的棱长总和
=棱长×12
10×12
=120 (cm)
长方体的表面积
=(长×宽+长×高+宽×高)×2
(20×6+20×10+10×6)×2
=380×2
=760 (cm )
下图中哪些是正方体的展开图?是的画“√”,不是的画“×”,可以利用附页2中的图2做一做。
2
选自教材第20~21页练习二
×
√
√
√
3
选自教材第20~21页练习二
淘气要把一个如下图所示的空包装箱的各面都贴上彩纸,至少需要多少平方厘米的彩纸 (单位:cm)
(40×25+40×40+40×25)×2=7200(平方厘米)
答:至少需要7200平方厘米的彩纸。
40
40
25
长方体的表面积
=(长×宽+长×高+宽×高)×2
选自教材第20~21页练习二
4
6个棱长都是20cm的正方体纸箱堆放在墙角处(如右图),露出多少个面?露在外面的面的面积是多少平方厘米?
方法一
一个一个地数
20×20×13=5200(平方厘米)
答:露出13个面,露在外面的面的面积是5200平方厘米。
选自教材第20~21页练习二
4
6个棱长都是20cm的正方体纸箱堆放在墙角处(如右图),露出多少个面?露在外面的面的面积是多少平方厘米?
从上、前、右三个角度数
方法二
20×20×13=5200(平方厘米)
答:露出13个面,露在外面的面的面积是5200平方厘米。
选自教材第20~21页练习二
5
将一个由5个棱长是10cm的正方体拼成的长方体拆开(如下图),5个正方体的表面积之和是多少?与长方体的表面积相等吗?与同伴交流。
求出一个小正方体的表面积×5
10×10×6×5=3000(平方厘米)
长方体的表面积:50×10×4+10×10×2=2200(平方厘米)
答:5个正方体的表面积之和是3000平方厘米,与长方体的表面积不相等。
方法一
选自教材第20~21页练习二
5
将一个由5个棱长是10cm的正方体拼成的长方体拆开(如下图),5个正方体的表面积之和是多少?与长方体的表面积相等吗?与同伴交流。
求出长方体的表面积+增加的面积
50×10×4+10×10×2+10×10×8=3000(平方厘米)
答:5个正方体的表面积之和是3000平方厘米。与长方体的表面积不相等。
方法二
选自教材第20~21页练习二
6
用同一种原材料做一个如右图的抽屉,至少需要多大面积的材料?(单位:dm)
(3.5×1.5+5×1.5)×2+3.5×5=43(平方分米)
答:至少需要43平方分米的材料。
这个长方体没有上面。
选自教材第20~21页练习二
7
如图,三种不同长度的小棒分别有12根、8根、4根,请你搭出3种不同的长方体或正方体,并填写下表。
序号 图形名称 长/cm 宽/cm 高/cm
选自教材第20~21页练习二
②
①
③
正方体
15
有两个面是正方形的长方体
10
10
8
长方体
15
10
8
15
15
8
一根绳子长10m,现要捆扎一种礼盒(如右图)。如果结头处要用掉绳子25cm,这根绳子最多可以捆扎几个这样的礼盒?(单位:cm)
选自教材第20~21页练习二
捆扎一个礼盒相当于:2个长,2个宽,4个高和1个结。
2×10+2×15+4×8+25=107(厘米)
10 m=1000 cm
1000÷107=9(个) ……37(厘米)
答:最多可以捆扎9个这样的礼盒。
1.做一个长2 m、宽1.5 m、高8 dm的长方体铁皮箱子,至少需要多少平方米铁皮?
注意统一单位。
8 dm=0.8 m
(2×1.5+2×0.8+1.5×0.8)×2
=5.8×2
=11.6(m )
答:至少需要11.6平方米铁皮。
2. 将两个一样的正方体木块拼成一个长方体木块,已知长方体木块的棱长总和是96 cm,原来两个正方体木块的棱长总和是多少厘米?
12×2=24 (条)
24-8=16 (条)
棱的条数:
答:原来两个正方体木块的棱长总和是144厘米。
96÷16=6 (cm)
12×6×2=144 (cm)
长方体和正方体都有8个顶点,6个面,12条棱
正方体是特殊的长方体
长方体的棱长总和=(长+宽+高)×4
正方体的棱长总和=棱长×12
这节课有什么收获呢?
长方体展开图由6个长方形(特殊情况下有2个正方形)组成,相对的面完全相同且隔开。
正方体由6个完全相同的正方形组成。
这节课有什么收获呢?
这节课有什么收获呢?
长方体或正方体6个面的面积之和,叫作它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长×棱长×6
堆放在墙角的正方体露在外面的面积的计算方法:
数出露在外面的面有几个,用一个面的面积乘露在外面的面的个数。
这节课有什么收获呢?
长方体和正方体的认识
长方体(一)
展开与折叠
露在外面的面
长方体和正方体的表面积
