四年级下册数学北师大版2.7认识三角形和四边形 练习二(课件)(共27张PPT)
文档属性
| 名称 | 四年级下册数学北师大版2.7认识三角形和四边形 练习二(课件)(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 17:12:24 | ||
图片预览



文档简介
(共27张PPT)
练习二
第二单元 认识三角形和四边形
认识三角形和四边形
01
三角形的分类
02
三角形的内角和
03
三角形的三边关系
04
四边形的分类
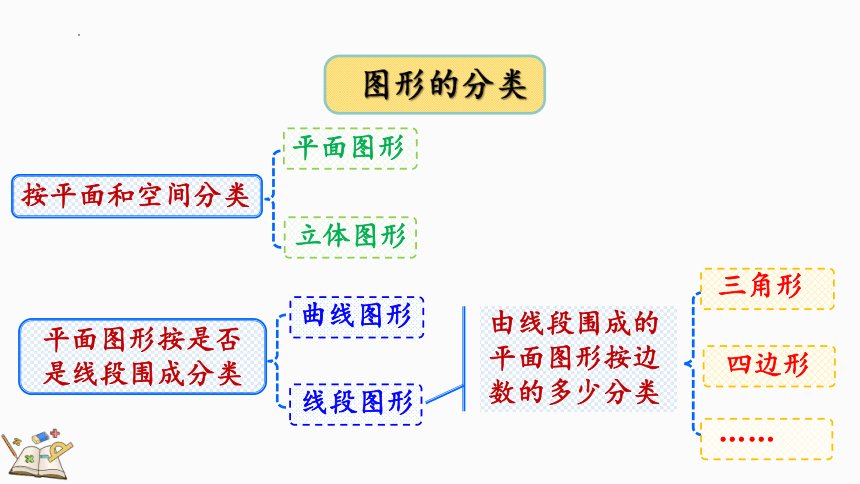
图形的分类
按平面和空间分类
平面图形
立体图形
平面图形按是否是线段围成分类
曲线图形
线段图形
由线段围成的平面图形按边数的多少分类
三角形
四边形
……
三角形的分类
按边分
按角分
锐角三角形
直角三角形
钝角三角形
三个锐角
一个直角,两个锐角
一个钝角,两个锐角
等腰三角形
等边三角形
两条边相等,两个角相等
三边相等,三个角相等
三角形的内角和等于180°。
三角形的任意两条边之和大于第三边。
三角形的特征
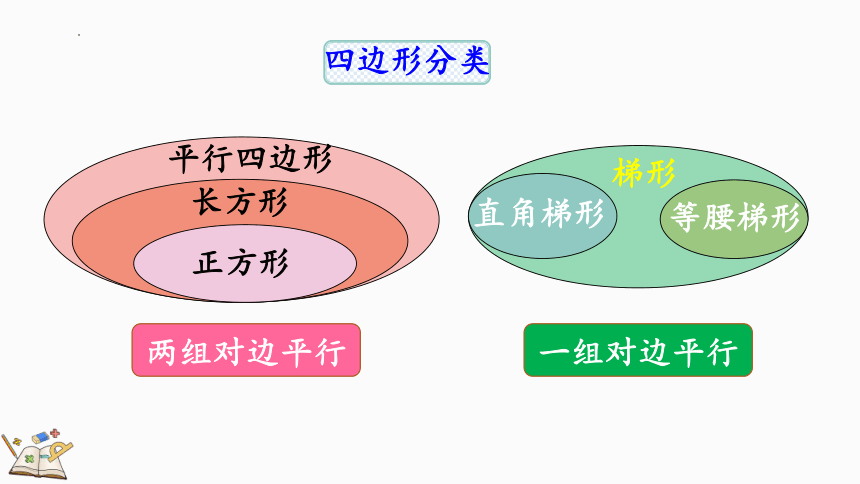
四边形分类
平行四边形
长方形
正方形
梯形
直角梯形
等腰梯形
两组对边平行
一组对边平行
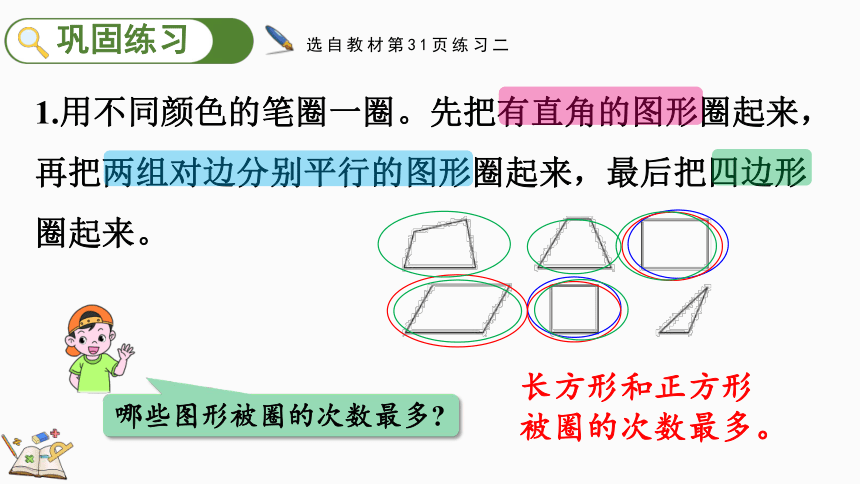
选自教材第31页练习二
哪些图形被圈的次数最多
1.用不同颜色的笔圈一圈。先把有直角的图形圈起来,再把两组对边分别平行的图形圈起来,最后把四边形圈起来。
长方形和正方形被圈的次数最多。
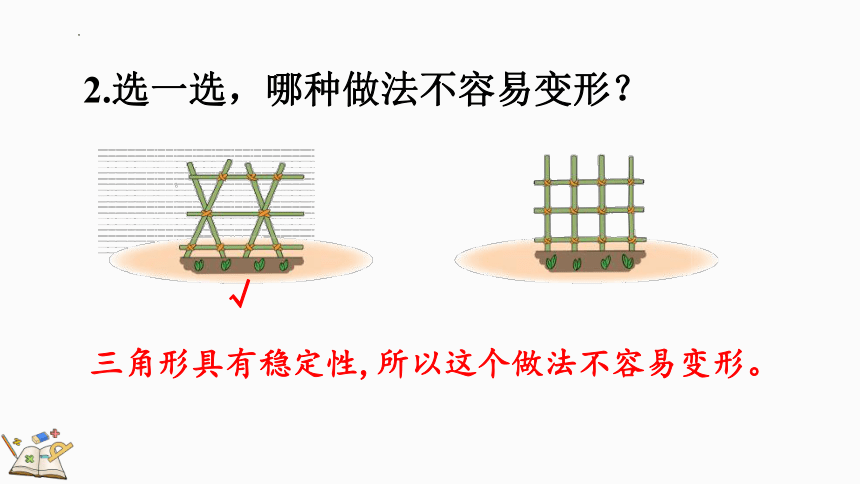
2.选一选,哪种做法不容易变形?
三角形具有稳定性,所以这个做法不容易变形。
√
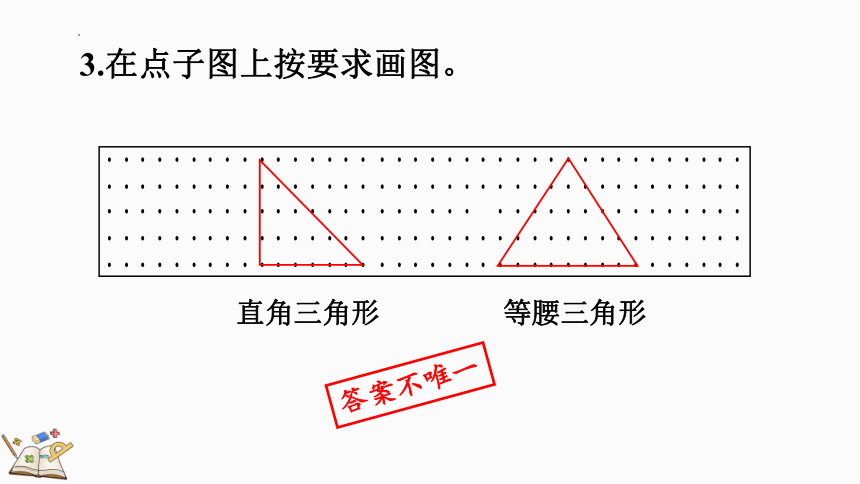
3.在点子图上按要求画图。
直角三角形
等腰三角形
答案不唯一
3.在点子图上按要求画图。
答案不唯一
梯形
平行四边形
4.在下面各图中画一条直线。
①
②
③
能分成两个直角三角形的是图__________。
能分成两个钝角三角形的是图__________。
能分成一个直角三角形和一个锐角三角形的是图__________。
①
②
③
5.下面图形各是什么三角形?
180°-40°-30°=110°
有一个钝角。
钝
180°-60°-30°=90°
有一个直角。
直
180°-70°-40°=70°
有三个锐角。
锐
6.在能摆成三角形的小棒下面画“√”。(单位:厘米)
√
√
√
(1)
(2)
(3)
(4)
3
4
5
2
2
6
5
3
3
3
3
3
三角形的较短的两边之和大于第三边。
7.用小棒照样子摆一摆。
摆1个三角形要3根小棒,
摆2个三角形要5根小棒,
摆5个三角形要( )根小棒。
11
你发现了什么?摆7个三角形要几根小棒呢?
3根 5根 7根 9根
三角形个数
小棒数量
规律
3
2+1
5
2×2+1
2×3+1
2×4+1
7
9
……
……
……
n个三角形
2n+1
2n+1
7.用小棒照样子摆一摆。
摆7个三角形要2×7+1=15根小棒!
8.猜一猜。
(1)
我拿的三角形没有钝角,它可能是什么三角形?
可能是……
可能是锐角三角形或直角三角形。
(2)下面哪组小棒能摆成等腰三角形?(单位:厘米)
√
因为较短的两条边的和大于第三边。
8.猜一猜。
(3)
有直角,两组对边分别平行的四边形是什么图形?
有直角,只有一组对边平行的四边形是什么图形?
可能是长方形或正方形。
是直角梯形。
8.猜一猜。
(1)三角形具有( )性,四边形具有( )性。
(2)两组对边分别平行的四边形是( )形,
只有一组对边平行的四边形是( )形。
(3)一个三角形中最多有( )个直角,最多有
( )个钝角,最多有( )个锐角,至少( )
个锐角。
(4)一个三角形的内角和是( ),扩大100倍后,
这个三角形的的内角和是( )。
1
1
3
2
1.填一填。
稳定
不稳定
平行四边
梯
180°
180°
2.求每个三角形中∠1的度数
∠1=?
∠1=?
∠1=?
35°
35°
1
1
1
27°
68°
28°
2.求每个三角形中∠1的度数
35°
35°
1
1
1
27°
68°
28°
∠1=180°-35°-35°=110°
2.求每个三角形中∠1的度数
35°
35°
1
1
1
27°
68°
28°
∠1=180°-90°-28°=62°
2.求每个三角形中∠1的度数
35°
35°
1
1
1
27°
68°
28°
∠1=180°-68°-27°=85°
3.数一数,填一填。
三角形有( )个;平行四边形有( )个;
梯形有( )个。
3
4
3
4.如果三角形的两条边的长分别是7厘米和5厘米,那么第三条边的长可能是几厘米?写出两种答案。
第三条边的长
7-5<
<7+5
2 <第三条边的长< 12
答:第三条边可能是4厘米、5厘米。
三角形的任意两条边的和大于第三边,任意两边的差小于第三边。
答案不唯一
这节课有什么收获呢?
1. 任意一个三角形的内角和都是180°。
2. 三角形中任意两条边的和,一定大于第三条边。
3. 三角形具有稳定性,平行四边形容易变形。
练习二
1.三角形的分类
2.三角形的内角和
3.三角形的三边关系
4.四边形的分类
练习二
第二单元 认识三角形和四边形
认识三角形和四边形
01
三角形的分类
02
三角形的内角和
03
三角形的三边关系
04
四边形的分类
图形的分类
按平面和空间分类
平面图形
立体图形
平面图形按是否是线段围成分类
曲线图形
线段图形
由线段围成的平面图形按边数的多少分类
三角形
四边形
……
三角形的分类
按边分
按角分
锐角三角形
直角三角形
钝角三角形
三个锐角
一个直角,两个锐角
一个钝角,两个锐角
等腰三角形
等边三角形
两条边相等,两个角相等
三边相等,三个角相等
三角形的内角和等于180°。
三角形的任意两条边之和大于第三边。
三角形的特征
四边形分类
平行四边形
长方形
正方形
梯形
直角梯形
等腰梯形
两组对边平行
一组对边平行
选自教材第31页练习二
哪些图形被圈的次数最多
1.用不同颜色的笔圈一圈。先把有直角的图形圈起来,再把两组对边分别平行的图形圈起来,最后把四边形圈起来。
长方形和正方形被圈的次数最多。
2.选一选,哪种做法不容易变形?
三角形具有稳定性,所以这个做法不容易变形。
√
3.在点子图上按要求画图。
直角三角形
等腰三角形
答案不唯一
3.在点子图上按要求画图。
答案不唯一
梯形
平行四边形
4.在下面各图中画一条直线。
①
②
③
能分成两个直角三角形的是图__________。
能分成两个钝角三角形的是图__________。
能分成一个直角三角形和一个锐角三角形的是图__________。
①
②
③
5.下面图形各是什么三角形?
180°-40°-30°=110°
有一个钝角。
钝
180°-60°-30°=90°
有一个直角。
直
180°-70°-40°=70°
有三个锐角。
锐
6.在能摆成三角形的小棒下面画“√”。(单位:厘米)
√
√
√
(1)
(2)
(3)
(4)
3
4
5
2
2
6
5
3
3
3
3
3
三角形的较短的两边之和大于第三边。
7.用小棒照样子摆一摆。
摆1个三角形要3根小棒,
摆2个三角形要5根小棒,
摆5个三角形要( )根小棒。
11
你发现了什么?摆7个三角形要几根小棒呢?
3根 5根 7根 9根
三角形个数
小棒数量
规律
3
2+1
5
2×2+1
2×3+1
2×4+1
7
9
……
……
……
n个三角形
2n+1
2n+1
7.用小棒照样子摆一摆。
摆7个三角形要2×7+1=15根小棒!
8.猜一猜。
(1)
我拿的三角形没有钝角,它可能是什么三角形?
可能是……
可能是锐角三角形或直角三角形。
(2)下面哪组小棒能摆成等腰三角形?(单位:厘米)
√
因为较短的两条边的和大于第三边。
8.猜一猜。
(3)
有直角,两组对边分别平行的四边形是什么图形?
有直角,只有一组对边平行的四边形是什么图形?
可能是长方形或正方形。
是直角梯形。
8.猜一猜。
(1)三角形具有( )性,四边形具有( )性。
(2)两组对边分别平行的四边形是( )形,
只有一组对边平行的四边形是( )形。
(3)一个三角形中最多有( )个直角,最多有
( )个钝角,最多有( )个锐角,至少( )
个锐角。
(4)一个三角形的内角和是( ),扩大100倍后,
这个三角形的的内角和是( )。
1
1
3
2
1.填一填。
稳定
不稳定
平行四边
梯
180°
180°
2.求每个三角形中∠1的度数
∠1=?
∠1=?
∠1=?
35°
35°
1
1
1
27°
68°
28°
2.求每个三角形中∠1的度数
35°
35°
1
1
1
27°
68°
28°
∠1=180°-35°-35°=110°
2.求每个三角形中∠1的度数
35°
35°
1
1
1
27°
68°
28°
∠1=180°-90°-28°=62°
2.求每个三角形中∠1的度数
35°
35°
1
1
1
27°
68°
28°
∠1=180°-68°-27°=85°
3.数一数,填一填。
三角形有( )个;平行四边形有( )个;
梯形有( )个。
3
4
3
4.如果三角形的两条边的长分别是7厘米和5厘米,那么第三条边的长可能是几厘米?写出两种答案。
第三条边的长
7-5<
<7+5
2 <第三条边的长< 12
答:第三条边可能是4厘米、5厘米。
三角形的任意两条边的和大于第三边,任意两边的差小于第三边。
答案不唯一
这节课有什么收获呢?
1. 任意一个三角形的内角和都是180°。
2. 三角形中任意两条边的和,一定大于第三条边。
3. 三角形具有稳定性,平行四边形容易变形。
练习二
1.三角形的分类
2.三角形的内角和
3.三角形的三边关系
4.四边形的分类
