人教版七年级数学下册 5.1相交线 同步练习(含答案)
文档属性
| 名称 | 人教版七年级数学下册 5.1相交线 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 135.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 20:15:55 | ||
图片预览



文档简介
七年级数学下册第五章5.1相交线 同步练习
一、填空题
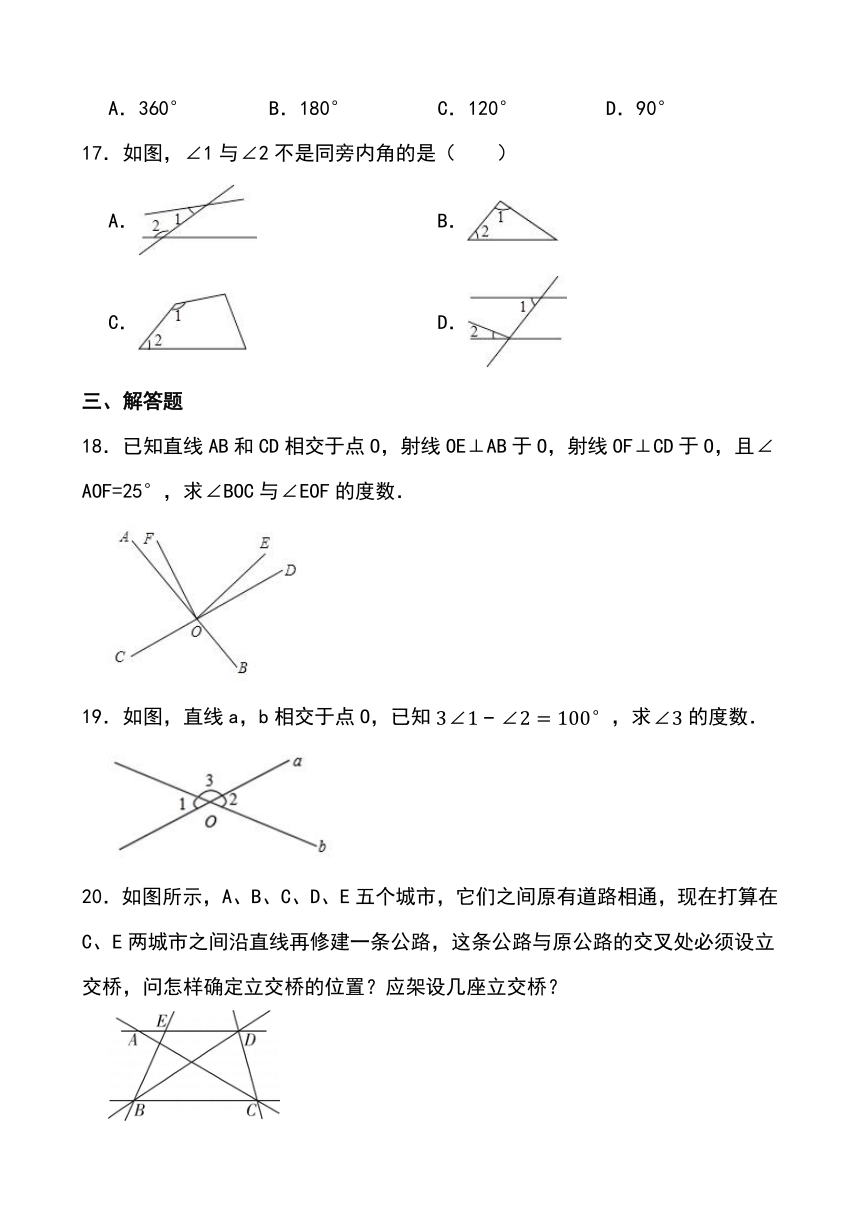
1.如图,农民伯伯若要将河里的水引到田地P处,需要从点P作河岸l的垂线,垂足是Q,则沿PQ挖的水沟最短,这样做的数学道理是 .
2.如图,O是直线AB上一点,已知∠1=36°,OD平分∠BOC,则∠AOD= .
3.如图所示,点P到l的垂线段为 ,P到l的距离为 cm.
4.如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE= 度.
5.直线,相交于点,,则直线,的夹角是 .
6.如图,直线AB与CD交于O点, ,则 = .
7.如图,直线AB、CD交于点O,OE⊥AB,∠EOC=40°,则∠BOD= 度.
8.如图,A,B,C,D在同一条直线上,AB=6,AD= AB,CD=1,则BC= .
二、单选题
9.如图所示,∠1和∠2是对顶角的是( )
A. B.
C. D.
10.如图,直线、相交,,则的度数( )
A. B. C. D.
11.如图,三角形ABC中,∠C=90°,AC=3,点P是BC边上一动点,则AP的长不可能是( )
A.3 B. C. D.4
12.如图,已知直线a,b被线段AB所截,则其中属于内错角的是( )
A.∠2和∠3 B.∠1和∠3 C.∠1和∠4 D.∠2和∠4
13.已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离为( )
A.4 cm B.5 cm C.小于2 cm D.不大于2 cm
14.如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
A.36° B.44° C.50° D.54°
15.已知:如图,AB⊥CD于O,EF为经过点O的一条直线,那么∠1与∠2的关系是( )
A.互为对顶角 B.互补 C.互余 D.相等
16.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=( )
A.360° B.180° C.120° D.90°
17.如图,∠1与∠2不是同旁内角的是( )
A. B.
C. D.
三、解答题
18.已知直线AB和CD相交于点O,射线OE⊥AB于O,射线OF⊥CD于O,且∠AOF=25°,求∠BOC与∠EOF的度数.
19.如图,直线a,b相交于点O,已知,求的度数.
20.如图所示,A、B、C、D、E五个城市,它们之间原有道路相通,现在打算在C、E两城市之间沿直线再修建一条公路,这条公路与原公路的交叉处必须设立交桥,问怎样确定立交桥的位置?应架设几座立交桥?
21.如图,直线AB,CD与直线EF分别交于点O,P.
(1)写出∠1的同位角,∠2的同旁内角和内错角;
(2)假设图形里面同位角的对数为a,同旁内角的对数为b,内错角的对数为c,则a+b+c等于多少?
(3)如果要知道图中8个角的度数,条件中至少应给出几个角的度数?
答案解析部分
1.垂线段最短
2.108°
3.1;1.2
4.25
5.
6.50
7.130
8.3
9.D
10.A
11.B
12.A
13.D
14.D
15.C
16.B
17.D
18.解:∵OF⊥CD,
∴∠FOD=90°.
∴∠AOD=∠AOF+∠FOD=25°+90°=115°.
∴∠BOC=115°.
∵OE⊥AB,
∴∠AOE=90°.
∴∠EOF=90°﹣25°=65°.
19.解:如图,
∵与是对顶角,
∴,
又∵,
∴,
∴,
∵与是邻补角,
∴,
∴.
∴的度数是.
20.解:连接CE,与BD的交点处架立交桥;1座.
21.解:(1)∠1的同位角是∠5,∠2的同旁内角是∠2,内错角是∠7;
(2)同位角有:∠1和∠5,∠3和∠7,∠2和∠6,∠4和∠8,共4对,故a=4;
同旁内角有:∠2和∠5,∠4和∠7,共2对,故b=2,
内错角有:∠2和∠7,∠4和∠5,共2对,故c=2,
a+b+c=4+2+2=8,
故答案为:8.
(3)要知道图中8个角的度数,条件中至少应给出∠2和∠5的度数,至少2个角度即可.
一、填空题
1.如图,农民伯伯若要将河里的水引到田地P处,需要从点P作河岸l的垂线,垂足是Q,则沿PQ挖的水沟最短,这样做的数学道理是 .
2.如图,O是直线AB上一点,已知∠1=36°,OD平分∠BOC,则∠AOD= .
3.如图所示,点P到l的垂线段为 ,P到l的距离为 cm.
4.如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE= 度.
5.直线,相交于点,,则直线,的夹角是 .
6.如图,直线AB与CD交于O点, ,则 = .
7.如图,直线AB、CD交于点O,OE⊥AB,∠EOC=40°,则∠BOD= 度.
8.如图,A,B,C,D在同一条直线上,AB=6,AD= AB,CD=1,则BC= .
二、单选题
9.如图所示,∠1和∠2是对顶角的是( )
A. B.
C. D.
10.如图,直线、相交,,则的度数( )
A. B. C. D.
11.如图,三角形ABC中,∠C=90°,AC=3,点P是BC边上一动点,则AP的长不可能是( )
A.3 B. C. D.4
12.如图,已知直线a,b被线段AB所截,则其中属于内错角的是( )
A.∠2和∠3 B.∠1和∠3 C.∠1和∠4 D.∠2和∠4
13.已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离为( )
A.4 cm B.5 cm C.小于2 cm D.不大于2 cm
14.如图,直线AB,CD相交于点O,EO⊥CD于点O,∠AOE=36°,则∠BOD=( )
A.36° B.44° C.50° D.54°
15.已知:如图,AB⊥CD于O,EF为经过点O的一条直线,那么∠1与∠2的关系是( )
A.互为对顶角 B.互补 C.互余 D.相等
16.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=( )
A.360° B.180° C.120° D.90°
17.如图,∠1与∠2不是同旁内角的是( )
A. B.
C. D.
三、解答题
18.已知直线AB和CD相交于点O,射线OE⊥AB于O,射线OF⊥CD于O,且∠AOF=25°,求∠BOC与∠EOF的度数.
19.如图,直线a,b相交于点O,已知,求的度数.
20.如图所示,A、B、C、D、E五个城市,它们之间原有道路相通,现在打算在C、E两城市之间沿直线再修建一条公路,这条公路与原公路的交叉处必须设立交桥,问怎样确定立交桥的位置?应架设几座立交桥?
21.如图,直线AB,CD与直线EF分别交于点O,P.
(1)写出∠1的同位角,∠2的同旁内角和内错角;
(2)假设图形里面同位角的对数为a,同旁内角的对数为b,内错角的对数为c,则a+b+c等于多少?
(3)如果要知道图中8个角的度数,条件中至少应给出几个角的度数?
答案解析部分
1.垂线段最短
2.108°
3.1;1.2
4.25
5.
6.50
7.130
8.3
9.D
10.A
11.B
12.A
13.D
14.D
15.C
16.B
17.D
18.解:∵OF⊥CD,
∴∠FOD=90°.
∴∠AOD=∠AOF+∠FOD=25°+90°=115°.
∴∠BOC=115°.
∵OE⊥AB,
∴∠AOE=90°.
∴∠EOF=90°﹣25°=65°.
19.解:如图,
∵与是对顶角,
∴,
又∵,
∴,
∴,
∵与是邻补角,
∴,
∴.
∴的度数是.
20.解:连接CE,与BD的交点处架立交桥;1座.
21.解:(1)∠1的同位角是∠5,∠2的同旁内角是∠2,内错角是∠7;
(2)同位角有:∠1和∠5,∠3和∠7,∠2和∠6,∠4和∠8,共4对,故a=4;
同旁内角有:∠2和∠5,∠4和∠7,共2对,故b=2,
内错角有:∠2和∠7,∠4和∠5,共2对,故c=2,
a+b+c=4+2+2=8,
故答案为:8.
(3)要知道图中8个角的度数,条件中至少应给出∠2和∠5的度数,至少2个角度即可.
