山东省济南市钢城区2023-2024学年八年级上学期期末数学试题(含答案)
文档属性
| 名称 | 山东省济南市钢城区2023-2024学年八年级上学期期末数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 893.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 20:26:06 | ||
图片预览




文档简介
2023—2024学年度上学期期末考试
初三数学试题
注意事项:
1.答卷前请考生务必在试卷的规定位置将自己的姓名、准考证号等内容填写准确。
2.本试题分第I卷(选择题) 和第Ⅱ卷(非选择题) 两部分,共150分,考试时间为 120分钟。
3.选择题每小题选出答案后, 用2B铅笔把答题卡上对应题目的答案标号涂黑; 非选择题用0.5mm黑色签字笔直接答在答题卡相应区域,不能答在试卷上; 解答题作图需用黑色签字笔,不能用铅笔。
4.考试结束后,由监考教师把答题卡收回。
第Ⅰ卷 (选择题40分)
一、选择题(本题共10小题,每小题选对得4分,选错、不选或选出的答案超过一个均记零分,共 40分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.要使分式 有意义,x应满足的条件是( )
A.x>-3 B.x<-3 C.x=-3 D.x≠-3
3.对甲、 乙、丙、丁四名选手进行射击测试,每人射击10次,平均成绩均为9.5环,方差如下表所示:则四名选手中成绩最稳定的是( )
选手 甲 乙 丙 丁
方差 1.34 0.16 2.56 0.21
A.甲 B.乙 C.丙 D.丁
4.如图,图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形, 则∠1+∠2+∠3+∠4+∠5的度数是( )
A.180° B.360° C.540° D.720°
5.计算 的结果是( )
6.一下列各选项中,因式分解正确的是( )
7.《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到 900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天, 则可列方程为( )
8.如图,在△ABC中, AB=BC=10, BD平分∠ABC交AC于点D,点F在BC上,且BF=4,连接AF, E为AF的中点, 连接DE, 则DE的长为( )
A.3 B.4 C.5 D.6
9.已知在平面直角坐标系中有三个点: A(-1, 2)、B(3, 1)、C(1, -2).在平面内确定点 D, 使得以A、B、C、D为顶点的四边形为平行四边形,则点D 的坐标不可能是( )
A.(1,5) D.(6,-4)
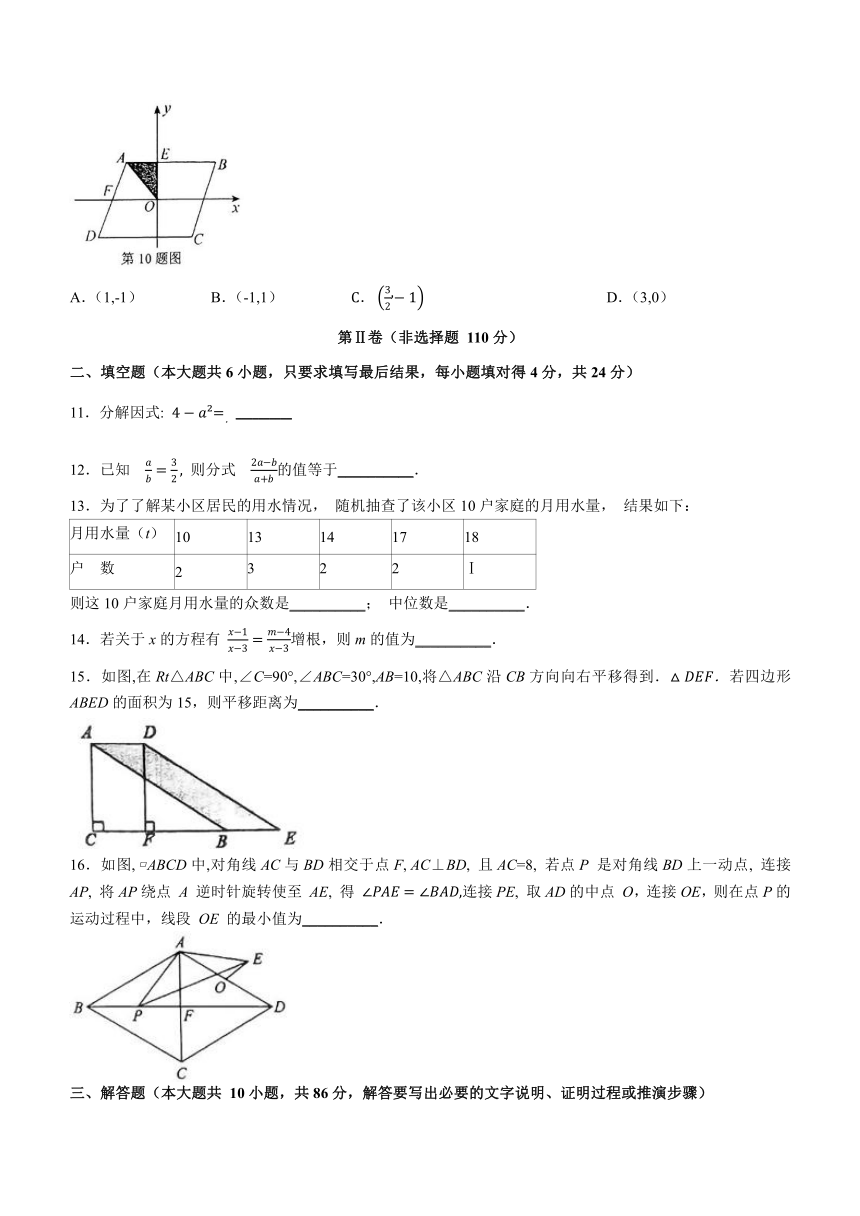
10.如图,原点O为 ABCD的对称中心,AB∥x轴,与y轴交于点E(0,1),AD与x轴交于 BE=2AE.若将△AOE绕原点O 顺时针旋转,每次旋转90°, 则第2024次旋转结束时, 点A的对应点的坐标( )
A.(1,-1) B.(-1,1) D.(3,0)
第Ⅱ卷(非选择题 110分)
二、填空题(本大题共6小题,只要求填写最后结果,每小题填对得4分,共24分)
11.分解因式:
12.已知 则分式 的值等于__________.
13.为了了解某小区居民的用水情况, 随机抽查了该小区10户家庭的月用水量, 结果如下:
月用水量(t) 10 13 14 17 18
户 数 2 3 2 2 Ⅰ
则这10户家庭月用水量的众数是__________; 中位数是__________.
14.若关于x的方程有 增根,则m的值为__________.
15.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=10,将△ABC沿CB方向向右平移得到.若四边形ABED的面积为15,则平移距离为__________.
16.如图, ABCD中,对角线AC与BD相交于点F, AC⊥BD, 且AC=8, 若点P 是对角线BD上一动点, 连接AP, 将AP绕点 A 逆时针旋转使至 AE, 得 连接PE, 取AD的中点 O,连接OE,则在点P的运动过程中,线段 OE 的最小值为__________.
三、解答题(本大题共 10小题,共86分,解答要写出必要的文字说明、证明过程或推演步骤)
17.(本题满分6分) 因式分解:
18.(本题满分6分) 解方程:
19.(本题满分6分) 先化简, 再求值: 其中x=2.
20.(本题满分8分)“五一”假期很多人都喜欢外出旅游,面对各大媒体报道出的各景区游客火爆的现象, 学校人文社团对 30个地区“五一”假期的出游人数进行了调查,获得了它们“五一”假期出游人数(出游人数用 m 表示,单位:百万)的数据,并对数据进行统计整理.数据分成5 组:
A 组: 1≤m<12; B 组:12≤m<23 ; C组:23≤m<34; D 组:34≤m<45 ;E组:45≤m<56下面给出了部分信息:
a.B组的数据:12, 13, 15, 16, 17, 17, 18, 20.
b.不完整的“五一”假期出游人数的频数分布直方图和扇形统计图如下:
请根据以上信息完成下列问题:
(1) 统计图中 E 组对应扇形百分比为n%, n= __________;
(2) 请补全频数分布直方图;
(3)这30个地区“五 ”假期出游人数的中位数是__________百万;
(4) 各组“五一”假期的平均出游人数如下表:
组别 A:1≤m<12 B:12≤m<23 C:23≤m<34 D:34≤m<45 E:45≤m<56
平均出游人数(百万) 5.5 16 32.5 42 50
求这30个地区“五一”假期的平均出游人数.
21.(本题满分8分) 已知:如图,点 O 为平行四边形 ABCD对角线AC 的中点,过点O的直线与AD, BC 分别相交于点 E, F. 求证:DE=BF.
22.(本题满分8分) 在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,△ABC是格点三角形(顶点在网格线的交点上).
(1) 作出△ABC关于原点 O成中心对称的△A B C ,并写出△A B C 三个顶点坐标A ( ), B ( ),C ( );
(2)把△A B C 向上平移4个单位长度得到.画出△A B C ;
(3)△A B C 与△ABC成中心对称,请直接写出对称中心的坐标( ).
23.(本题满分 10分)“春节”期间,某电商想购进A、 B两种商品出售, 已知每件B种商品的进价比每件 A 种商品的进价少5元,且用400元购进 A 种商品的数量是用 100元购进B种商品数量的2倍.
(1)求每件 A 种商品和每件 B 种商品的进价分别是多少元
(2)商店决定购进A、B两种商品共80件,A种商品加价5 元出售,B种商品比进价提高20%后出售,要使所有商品全部出售后利润不少于 200元,求A种商品至少购进多少件
24.(本题满分 10分) 阅读材料:教科书中提到 和 这样的式子叫做完全平方式.”有些多项式不是完全平方式,我们可以通过添加项,凑成完全平方式,再减去这个添加项,使整个式子的值不变,这样也可以将多项式进行分解,并解决一些最值问题.
例如: (1) 分解因式:
(2) 求代数式 的最小值.
∴当.时,代数式 有最小值
结合以上材料解决下面的问题:
(1)若二次三项式 恰好是完全平方式,k的值是 ;
(2)分解因式:
(3)当x为何值时, 有最小值 最小值是多少
25、 (本题满分12分) 综合与实践
问题背景:几何学的产生,源于人们对土地面积测量的需要,可以说几何学从一开始便与面积结下了不解之缘.我们已经掌握了平行四边形面积的求法,但是一般四边形的面积往往不易求得,那么我们能否将其转化为平行四边形来求呢
问题解决:下面是两位同学的转化方法:
方法1:如图1,连接四边形ABCD的对角线AC,BD,分别过四边形 ABCD的四个顶点作对角线的平行线,所作四条线相交形成四边形EFGH,易证四边形EFGH 是平行四边形.
(1)请直接写出 S 四边形ABCD和 之间的数量关系: .
方法2: 如图2, 取四边形ABCD四边的中点E, F, G, H, 连接EF , FG , GH, HE,
(2) 请直接写出S 四边形ABCD与 之间数量的关系: .
(3) 求证: 四边形EFGH是平行四边形;
实践应用:
如图3,某村有一个四边形池塘, 它的四个顶点A,B,C,D处均有一棵大树,村里准备开挖池塘建鱼塘,想使池塘的面积扩大一倍,又想保持大树不动,并要求扩建后的池塘成平行四边形的形状.
(4)请问能否实现这一设想 若能,请你画出你设计的图形; 若不能,请说明理由.
(5)已知, 在四边形池塘ABCD中, 对角线AC与BD交于点O,.则求四边形池塘 ABCD的面积.
26.(本题满分 12分)
问题情景:老师让同学们以“两个大小不等的等腰直角三角板的直角顶点重合,并让一个三角板固定,另一个绕直角顶点旋转”为主题开展数学活动.如图1, 和 都是等腰直角三角形, 点D, E分别在边BC, AC上, 连接AD, 点M, P, N分别为DE, AD, AB的中点.试判断线段PM与PN的数量关系和位置关系.
问题探究:
(1) 甲小组发现:图1中,线段PM与PN的数量关系是 位置关系 ;
(2)乙小组受到甲小组的启发,继续进行探究,把 绕点C逆时针方向旋转到如图2的位置,请判断 的形状并证明;
问题拓展:
(3) 两小组的同学继续探究:把 绕点C在平面内自由旋转,当( 时,直接写出线段MN长度的最大值.
2023─2024学年度上学期期末考试
初三数学试题参考答案:
一、选择题(每小题4分,共40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B B C C A A D B
二、填空题(每小题4分,共24分)
11. 12. 13.13 13.5 14.6 15.3 16.2
17.(1)(3分)解::
(2)(3分)解:
18.(6分)解:去分母得:, 2
去括号得:, 3
移项合并得:, 4
解得:, 5
经检验是增根,分式方程无解. 6
19.(6)解:原式 2
3
4
当时,原式. 6
20.(每小题2分)
补全频数直方图如下:
(1)10 2
(2)D组: (个) 3
C组: (个) 4
(3)15.5百万 6
(4) (百万). 8分
答:这30个地区五一平均出游人数是20百万
21.(8)证明:∵四边形ABCD是平行四边形
∴, 2
∴ 4
∵点O为对角线AC的中点,∴ 5
在, 6
∴, 7
∴,∴ 8
22.(1)解:如图,为所求作的三角形:
根据图可知, 3分
(2)解:如图,为所求作的三角形:
6分
(3)解:连接,则的交点即为对称中心,
∵,
∴对称中心的坐标为.
即对称中心的坐标为.
故答案为:. 8分
23.(10)(1)解:设每件A商品的进价为x元,则每件B商品的进价为元, 1
根据题意,得, 2
解这个方程,得, 3
经检验,是原分式方程的解,且符合题意, 4
则, 5
答:每件A商品的进价为10元,每件B商品的进价为5元;
(2)解:设购进A商品a件,则购进B商品件, 6
由题意,可得, 8
解得,
答:A种商品至少购进30件. 10
24.【答案】(1)或 2分
(2); 6分
(3)∵
∴当时,有最小值. 10分
25.(10分)【答案】(1); 1分
分析:(1):如图,
∵,
∴四边形AEBO,四边形BFCO,四边形CGDO,四边形DHAO都是平行四边形
∴,
∴
故答案为
(2):如图,连接BD.
(2) 2分
∵E,H分别为AB,AD中点
∴..
∴,
∴
故答案为
(3)证明:∵E,H分别为AB,AD中点
∴.,
∵F,G分别为BC,CD中点
∴.
∴
∴四边形EFGH为平行四边形 5分
应用:(4)能,如图所示,连接对角线AC,BD交于点O,
过点D作AC的平行线,过点B作AC的平行线
过点A作BD的平行线,过点C作BD的平行线
四边形EHGF即为所求
7分
应用(2)过H作于点M,
∵,∴,
∵,∴,
∴ (或写为)
∴ (或写为)
∴,(或写为)
故答案为.(或写为) 10分
26.(1) 2分
(2)证明:连接BD,由旋转知,
∵,∴
∴
∵点P,M,N分别是AD,ED,AB的中点,
∴PN,PM分别是,的中位线
∴
∴
∴是等腰三角形
又∵,
∴,
∵,
∴
∵,∴,
∴,
∴是等腰直角三角形: 7分
(3)由(2)知,是等腰直角三角形,,
∴点D在BC的延长线上时,PM有最大值,
∴,∵,
∵(或). 12分
初三数学试题
注意事项:
1.答卷前请考生务必在试卷的规定位置将自己的姓名、准考证号等内容填写准确。
2.本试题分第I卷(选择题) 和第Ⅱ卷(非选择题) 两部分,共150分,考试时间为 120分钟。
3.选择题每小题选出答案后, 用2B铅笔把答题卡上对应题目的答案标号涂黑; 非选择题用0.5mm黑色签字笔直接答在答题卡相应区域,不能答在试卷上; 解答题作图需用黑色签字笔,不能用铅笔。
4.考试结束后,由监考教师把答题卡收回。
第Ⅰ卷 (选择题40分)
一、选择题(本题共10小题,每小题选对得4分,选错、不选或选出的答案超过一个均记零分,共 40分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.要使分式 有意义,x应满足的条件是( )
A.x>-3 B.x<-3 C.x=-3 D.x≠-3
3.对甲、 乙、丙、丁四名选手进行射击测试,每人射击10次,平均成绩均为9.5环,方差如下表所示:则四名选手中成绩最稳定的是( )
选手 甲 乙 丙 丁
方差 1.34 0.16 2.56 0.21
A.甲 B.乙 C.丙 D.丁
4.如图,图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形, 则∠1+∠2+∠3+∠4+∠5的度数是( )
A.180° B.360° C.540° D.720°
5.计算 的结果是( )
6.一下列各选项中,因式分解正确的是( )
7.《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到 900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天, 则可列方程为( )
8.如图,在△ABC中, AB=BC=10, BD平分∠ABC交AC于点D,点F在BC上,且BF=4,连接AF, E为AF的中点, 连接DE, 则DE的长为( )
A.3 B.4 C.5 D.6
9.已知在平面直角坐标系中有三个点: A(-1, 2)、B(3, 1)、C(1, -2).在平面内确定点 D, 使得以A、B、C、D为顶点的四边形为平行四边形,则点D 的坐标不可能是( )
A.(1,5) D.(6,-4)
10.如图,原点O为 ABCD的对称中心,AB∥x轴,与y轴交于点E(0,1),AD与x轴交于 BE=2AE.若将△AOE绕原点O 顺时针旋转,每次旋转90°, 则第2024次旋转结束时, 点A的对应点的坐标( )
A.(1,-1) B.(-1,1) D.(3,0)
第Ⅱ卷(非选择题 110分)
二、填空题(本大题共6小题,只要求填写最后结果,每小题填对得4分,共24分)
11.分解因式:
12.已知 则分式 的值等于__________.
13.为了了解某小区居民的用水情况, 随机抽查了该小区10户家庭的月用水量, 结果如下:
月用水量(t) 10 13 14 17 18
户 数 2 3 2 2 Ⅰ
则这10户家庭月用水量的众数是__________; 中位数是__________.
14.若关于x的方程有 增根,则m的值为__________.
15.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=10,将△ABC沿CB方向向右平移得到.若四边形ABED的面积为15,则平移距离为__________.
16.如图, ABCD中,对角线AC与BD相交于点F, AC⊥BD, 且AC=8, 若点P 是对角线BD上一动点, 连接AP, 将AP绕点 A 逆时针旋转使至 AE, 得 连接PE, 取AD的中点 O,连接OE,则在点P的运动过程中,线段 OE 的最小值为__________.
三、解答题(本大题共 10小题,共86分,解答要写出必要的文字说明、证明过程或推演步骤)
17.(本题满分6分) 因式分解:
18.(本题满分6分) 解方程:
19.(本题满分6分) 先化简, 再求值: 其中x=2.
20.(本题满分8分)“五一”假期很多人都喜欢外出旅游,面对各大媒体报道出的各景区游客火爆的现象, 学校人文社团对 30个地区“五一”假期的出游人数进行了调查,获得了它们“五一”假期出游人数(出游人数用 m 表示,单位:百万)的数据,并对数据进行统计整理.数据分成5 组:
A 组: 1≤m<12; B 组:12≤m<23 ; C组:23≤m<34; D 组:34≤m<45 ;E组:45≤m<56下面给出了部分信息:
a.B组的数据:12, 13, 15, 16, 17, 17, 18, 20.
b.不完整的“五一”假期出游人数的频数分布直方图和扇形统计图如下:
请根据以上信息完成下列问题:
(1) 统计图中 E 组对应扇形百分比为n%, n= __________;
(2) 请补全频数分布直方图;
(3)这30个地区“五 ”假期出游人数的中位数是__________百万;
(4) 各组“五一”假期的平均出游人数如下表:
组别 A:1≤m<12 B:12≤m<23 C:23≤m<34 D:34≤m<45 E:45≤m<56
平均出游人数(百万) 5.5 16 32.5 42 50
求这30个地区“五一”假期的平均出游人数.
21.(本题满分8分) 已知:如图,点 O 为平行四边形 ABCD对角线AC 的中点,过点O的直线与AD, BC 分别相交于点 E, F. 求证:DE=BF.
22.(本题满分8分) 在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,△ABC是格点三角形(顶点在网格线的交点上).
(1) 作出△ABC关于原点 O成中心对称的△A B C ,并写出△A B C 三个顶点坐标A ( ), B ( ),C ( );
(2)把△A B C 向上平移4个单位长度得到.画出△A B C ;
(3)△A B C 与△ABC成中心对称,请直接写出对称中心的坐标( ).
23.(本题满分 10分)“春节”期间,某电商想购进A、 B两种商品出售, 已知每件B种商品的进价比每件 A 种商品的进价少5元,且用400元购进 A 种商品的数量是用 100元购进B种商品数量的2倍.
(1)求每件 A 种商品和每件 B 种商品的进价分别是多少元
(2)商店决定购进A、B两种商品共80件,A种商品加价5 元出售,B种商品比进价提高20%后出售,要使所有商品全部出售后利润不少于 200元,求A种商品至少购进多少件
24.(本题满分 10分) 阅读材料:教科书中提到 和 这样的式子叫做完全平方式.”有些多项式不是完全平方式,我们可以通过添加项,凑成完全平方式,再减去这个添加项,使整个式子的值不变,这样也可以将多项式进行分解,并解决一些最值问题.
例如: (1) 分解因式:
(2) 求代数式 的最小值.
∴当.时,代数式 有最小值
结合以上材料解决下面的问题:
(1)若二次三项式 恰好是完全平方式,k的值是 ;
(2)分解因式:
(3)当x为何值时, 有最小值 最小值是多少
25、 (本题满分12分) 综合与实践
问题背景:几何学的产生,源于人们对土地面积测量的需要,可以说几何学从一开始便与面积结下了不解之缘.我们已经掌握了平行四边形面积的求法,但是一般四边形的面积往往不易求得,那么我们能否将其转化为平行四边形来求呢
问题解决:下面是两位同学的转化方法:
方法1:如图1,连接四边形ABCD的对角线AC,BD,分别过四边形 ABCD的四个顶点作对角线的平行线,所作四条线相交形成四边形EFGH,易证四边形EFGH 是平行四边形.
(1)请直接写出 S 四边形ABCD和 之间的数量关系: .
方法2: 如图2, 取四边形ABCD四边的中点E, F, G, H, 连接EF , FG , GH, HE,
(2) 请直接写出S 四边形ABCD与 之间数量的关系: .
(3) 求证: 四边形EFGH是平行四边形;
实践应用:
如图3,某村有一个四边形池塘, 它的四个顶点A,B,C,D处均有一棵大树,村里准备开挖池塘建鱼塘,想使池塘的面积扩大一倍,又想保持大树不动,并要求扩建后的池塘成平行四边形的形状.
(4)请问能否实现这一设想 若能,请你画出你设计的图形; 若不能,请说明理由.
(5)已知, 在四边形池塘ABCD中, 对角线AC与BD交于点O,.则求四边形池塘 ABCD的面积.
26.(本题满分 12分)
问题情景:老师让同学们以“两个大小不等的等腰直角三角板的直角顶点重合,并让一个三角板固定,另一个绕直角顶点旋转”为主题开展数学活动.如图1, 和 都是等腰直角三角形, 点D, E分别在边BC, AC上, 连接AD, 点M, P, N分别为DE, AD, AB的中点.试判断线段PM与PN的数量关系和位置关系.
问题探究:
(1) 甲小组发现:图1中,线段PM与PN的数量关系是 位置关系 ;
(2)乙小组受到甲小组的启发,继续进行探究,把 绕点C逆时针方向旋转到如图2的位置,请判断 的形状并证明;
问题拓展:
(3) 两小组的同学继续探究:把 绕点C在平面内自由旋转,当( 时,直接写出线段MN长度的最大值.
2023─2024学年度上学期期末考试
初三数学试题参考答案:
一、选择题(每小题4分,共40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B B C C A A D B
二、填空题(每小题4分,共24分)
11. 12. 13.13 13.5 14.6 15.3 16.2
17.(1)(3分)解::
(2)(3分)解:
18.(6分)解:去分母得:, 2
去括号得:, 3
移项合并得:, 4
解得:, 5
经检验是增根,分式方程无解. 6
19.(6)解:原式 2
3
4
当时,原式. 6
20.(每小题2分)
补全频数直方图如下:
(1)10 2
(2)D组: (个) 3
C组: (个) 4
(3)15.5百万 6
(4) (百万). 8分
答:这30个地区五一平均出游人数是20百万
21.(8)证明:∵四边形ABCD是平行四边形
∴, 2
∴ 4
∵点O为对角线AC的中点,∴ 5
在, 6
∴, 7
∴,∴ 8
22.(1)解:如图,为所求作的三角形:
根据图可知, 3分
(2)解:如图,为所求作的三角形:
6分
(3)解:连接,则的交点即为对称中心,
∵,
∴对称中心的坐标为.
即对称中心的坐标为.
故答案为:. 8分
23.(10)(1)解:设每件A商品的进价为x元,则每件B商品的进价为元, 1
根据题意,得, 2
解这个方程,得, 3
经检验,是原分式方程的解,且符合题意, 4
则, 5
答:每件A商品的进价为10元,每件B商品的进价为5元;
(2)解:设购进A商品a件,则购进B商品件, 6
由题意,可得, 8
解得,
答:A种商品至少购进30件. 10
24.【答案】(1)或 2分
(2); 6分
(3)∵
∴当时,有最小值. 10分
25.(10分)【答案】(1); 1分
分析:(1):如图,
∵,
∴四边形AEBO,四边形BFCO,四边形CGDO,四边形DHAO都是平行四边形
∴,
∴
故答案为
(2):如图,连接BD.
(2) 2分
∵E,H分别为AB,AD中点
∴..
∴,
∴
故答案为
(3)证明:∵E,H分别为AB,AD中点
∴.,
∵F,G分别为BC,CD中点
∴.
∴
∴四边形EFGH为平行四边形 5分
应用:(4)能,如图所示,连接对角线AC,BD交于点O,
过点D作AC的平行线,过点B作AC的平行线
过点A作BD的平行线,过点C作BD的平行线
四边形EHGF即为所求
7分
应用(2)过H作于点M,
∵,∴,
∵,∴,
∴ (或写为)
∴ (或写为)
∴,(或写为)
故答案为.(或写为) 10分
26.(1) 2分
(2)证明:连接BD,由旋转知,
∵,∴
∴
∵点P,M,N分别是AD,ED,AB的中点,
∴PN,PM分别是,的中位线
∴
∴
∴是等腰三角形
又∵,
∴,
∵,
∴
∵,∴,
∴,
∴是等腰直角三角形: 7分
(3)由(2)知,是等腰直角三角形,,
∴点D在BC的延长线上时,PM有最大值,
∴,∵,
∵(或). 12分
同课章节目录
