17.1 勾股定理(第3课时)教学课件--人教版初中数学八下
文档属性
| 名称 | 17.1 勾股定理(第3课时)教学课件--人教版初中数学八下 |  | |
| 格式 | pptx | ||
| 文件大小 | 640.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:40 | ||
图片预览




文档简介
(共18张PPT)
第 十七章 勾股定理
第十七章 勾股定理
17.1 勾股定理
第三课时 利用勾股定理作图或计算
学 习 目 标
1
2
会运用勾股定理确定数轴上表示实数的点及解决网格问题. (重点)
能灵活运用勾股定理进行计算,并会解决相应的折叠问题. (难点)
新课导入
知识回顾
实数
数轴上的点
一一对应
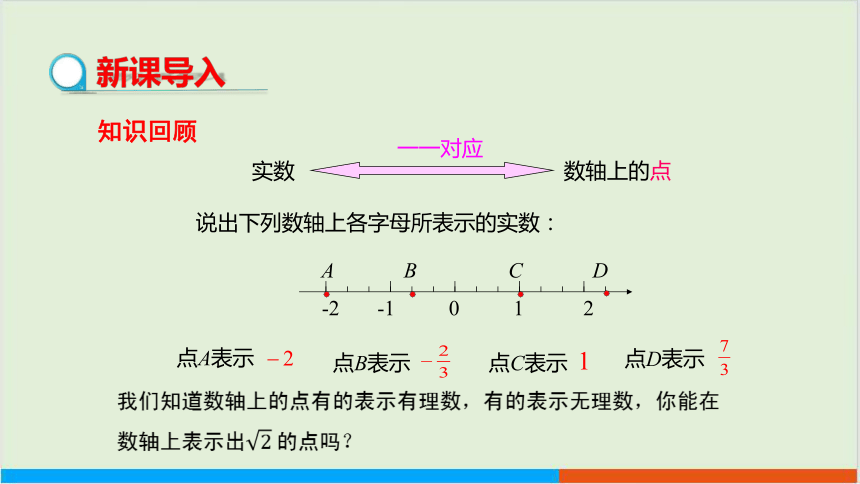
说出下列数轴上各字母所表示的实数:
A B C D
-2 -1 0 1 2
点C表示
点D表示
点B表示
点A表示
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上表示出的点吗?
知识讲解
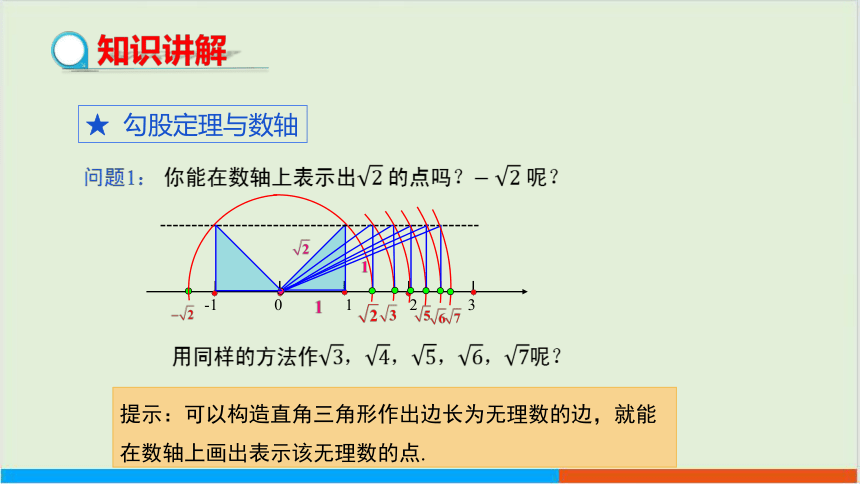
★ 勾股定理与数轴
-1 0 1 2 3
问题1: 你能在数轴上表示出的点吗? 呢?
用同样的方法作呢?
提示:可以构造直角三角形作出边长为无理数的边,就能在数轴上画出表示该无理数的点.
思考:根据上面问题你能在数轴上画出表示的点吗?
√
√
问题2 :长为的线段能是直角边的长都为正整数的直角三角形的斜边吗?
0
1
2
3
4
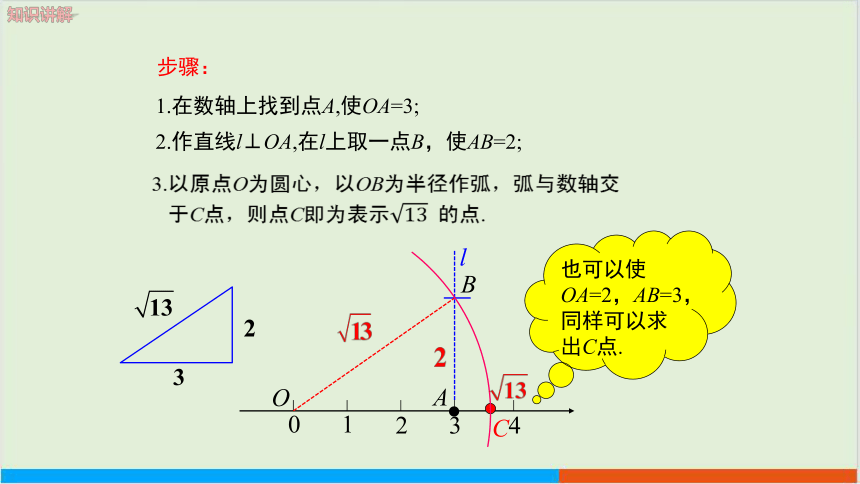
步骤:
l
A
B
C
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交
于C点,则点C即为表示的点.
O
也可以使OA=2,AB=3,同样可以求出C点.
归纳总结
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
类似地,利用勾股定理可以作出长为 的线段.
类比迁移
“数学海螺”
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
例1 如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边为1和2,
∴斜边长为 ,
即-1到A的距离是 ,
∴点A所表示的数为 .
易错点:求点表示的数时注意画弧的起点不从原点起,因而所表示的数不是斜边长.
★ 勾股定理与网格
B
B
B
画一画 :在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中从A出发画出长度分别为的线段AB.
归纳总结:勾股定理与网格的综合求线段长时,通常是把线段放在与网格构成的直角三角形中,利用勾股定理求其长度.
例2 如图,每个小方格都是边长为1的正方形,求△ABC的周长.
分析:利用正方形网格中有90°角的特点,把△ABC的三边分别作为三个直角三角形的斜边, 利用勾股定理求出△ABC的三边长,进而求出其周长.
解:∵
,
∴ △ ABC的周长= .
★ 勾股定理与图形的计算
例3 如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
解:在Rt△ABF中,由勾股定理得 BF2=AF2-AB2=102-82=36,
∴BF=6cm.∴CF=BC-BF=4.
设EC=xcm,则EF=DE=(8-x)cm ,
在Rt△ECF中,根据勾股定理
得 x2+ 42=(8-x)2,解得 x=3.
即EC的长为3cm.
折叠问题中结合勾股定理求线段长的方法:
(1)设一条未知线段的长为x(一般设所求线段的长为x);
(2)用已知线段长或含x的代数式表示出其他线段长;
(3)在一个直角三角形中应用勾股定理列出一个关于x
的方程;
(4)解这个方程,从而求出所求线段长.
归纳总结
随堂训练
B
A
1.如图所示:数轴上点A所表示的数为a,则a的值是( )
A.+1 B. -1 C.- +1 D.- -1
2.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A. B. C. D.
3.如图,在一张长方形ABCD纸张中,一边BC折叠后落在对角线BD上,点E为折痕与边CD的交点,若AB=5,BC=12,求图中阴影部分的面积。
解:因为BC折叠后落在对角线BD上,设C的对应点是F,则EF⊥BD,△DEF是直角三角形,∠DFE=90°.
因为BD是长方形ABCD的对角线,
所以BD==13,DF=13-12=1,
设CE=x,则EF=CE=x,DE=5-x,
在△DEF中,+12=,解得x=,
所以图中阴影部分的面积.
F
解:∵AB=AD=8cm,∠A=60°,
∴△ABD是等边三角形.
∵∠ADC=150°,∴∠CDB=150°-60°=90°,
∴△BCD是直角三角形.
又∵四边形的周长为32cm,
∴CD+BC=32-AD-AB=32-8-8=16(cm).
设CD=x,则BC=16-x,
由勾股定理得82+x2=(16-x)2
解得x=6cm.∴S△BCD= ×6×8=24(cm)2.
4.如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32cm,求△BCD的面积.
课堂小结
利用勾股定理作图或计算
在数轴上表示无理数的点
利用勾股定理解网格中的问题
利用勾股定理解折叠问题或其他图形问题
第 十七章 勾股定理
第十七章 勾股定理
17.1 勾股定理
第三课时 利用勾股定理作图或计算
学 习 目 标
1
2
会运用勾股定理确定数轴上表示实数的点及解决网格问题. (重点)
能灵活运用勾股定理进行计算,并会解决相应的折叠问题. (难点)
新课导入
知识回顾
实数
数轴上的点
一一对应
说出下列数轴上各字母所表示的实数:
A B C D
-2 -1 0 1 2
点C表示
点D表示
点B表示
点A表示
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上表示出的点吗?
知识讲解
★ 勾股定理与数轴
-1 0 1 2 3
问题1: 你能在数轴上表示出的点吗? 呢?
用同样的方法作呢?
提示:可以构造直角三角形作出边长为无理数的边,就能在数轴上画出表示该无理数的点.
思考:根据上面问题你能在数轴上画出表示的点吗?
√
√
问题2 :长为的线段能是直角边的长都为正整数的直角三角形的斜边吗?
0
1
2
3
4
步骤:
l
A
B
C
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交
于C点,则点C即为表示的点.
O
也可以使OA=2,AB=3,同样可以求出C点.
归纳总结
利用勾股定理表示无理数的方法:
(1)利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
(2)以原点为圆心,以无理数斜边长为半径画弧与数轴存在交点,在原点左边的点表示是负无理数,在原点右边的点表示是正无理数.
类似地,利用勾股定理可以作出长为 的线段.
类比迁移
“数学海螺”
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
例1 如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边为1和2,
∴斜边长为 ,
即-1到A的距离是 ,
∴点A所表示的数为 .
易错点:求点表示的数时注意画弧的起点不从原点起,因而所表示的数不是斜边长.
★ 勾股定理与网格
B
B
B
画一画 :在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中从A出发画出长度分别为的线段AB.
归纳总结:勾股定理与网格的综合求线段长时,通常是把线段放在与网格构成的直角三角形中,利用勾股定理求其长度.
例2 如图,每个小方格都是边长为1的正方形,求△ABC的周长.
分析:利用正方形网格中有90°角的特点,把△ABC的三边分别作为三个直角三角形的斜边, 利用勾股定理求出△ABC的三边长,进而求出其周长.
解:∵
,
∴ △ ABC的周长= .
★ 勾股定理与图形的计算
例3 如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
解:在Rt△ABF中,由勾股定理得 BF2=AF2-AB2=102-82=36,
∴BF=6cm.∴CF=BC-BF=4.
设EC=xcm,则EF=DE=(8-x)cm ,
在Rt△ECF中,根据勾股定理
得 x2+ 42=(8-x)2,解得 x=3.
即EC的长为3cm.
折叠问题中结合勾股定理求线段长的方法:
(1)设一条未知线段的长为x(一般设所求线段的长为x);
(2)用已知线段长或含x的代数式表示出其他线段长;
(3)在一个直角三角形中应用勾股定理列出一个关于x
的方程;
(4)解这个方程,从而求出所求线段长.
归纳总结
随堂训练
B
A
1.如图所示:数轴上点A所表示的数为a,则a的值是( )
A.+1 B. -1 C.- +1 D.- -1
2.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A. B. C. D.
3.如图,在一张长方形ABCD纸张中,一边BC折叠后落在对角线BD上,点E为折痕与边CD的交点,若AB=5,BC=12,求图中阴影部分的面积。
解:因为BC折叠后落在对角线BD上,设C的对应点是F,则EF⊥BD,△DEF是直角三角形,∠DFE=90°.
因为BD是长方形ABCD的对角线,
所以BD==13,DF=13-12=1,
设CE=x,则EF=CE=x,DE=5-x,
在△DEF中,+12=,解得x=,
所以图中阴影部分的面积.
F
解:∵AB=AD=8cm,∠A=60°,
∴△ABD是等边三角形.
∵∠ADC=150°,∴∠CDB=150°-60°=90°,
∴△BCD是直角三角形.
又∵四边形的周长为32cm,
∴CD+BC=32-AD-AB=32-8-8=16(cm).
设CD=x,则BC=16-x,
由勾股定理得82+x2=(16-x)2
解得x=6cm.∴S△BCD= ×6×8=24(cm)2.
4.如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32cm,求△BCD的面积.
课堂小结
利用勾股定理作图或计算
在数轴上表示无理数的点
利用勾股定理解网格中的问题
利用勾股定理解折叠问题或其他图形问题
