18.1.2 平行四边形的判定(第1课时)教学课件--人教版初中数学八下
文档属性
| 名称 | 18.1.2 平行四边形的判定(第1课时)教学课件--人教版初中数学八下 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:40 | ||
图片预览





文档简介
(共15张PPT)
第十八章 平行四边形
18.1.2 平行四边形的判定
第1课时
第十八章 平行四边形
学 习 目 标
通过平行四边形判定定理的猜想与证明过程,体会类比思想及探究图形判定的一般思路.
掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理.(难点)
1
2
新课导入
学行四边形之后,小明回家用细木棒钉制了一个平行四边形.第二天,小明拿着自己动手做的平行四边形向同学们展示.
小红却问:你凭什么确定这四边形就是平行四边形呢
大家议论纷纷……
小强提议说:我们可以度量它的边,如果它的两组对边分别相等,那么它就是一个平行四边形.
小伟提议说:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形.
小丽却说:我们可以度量它的对角线,如果它的对角线互相平分,那么它就是一个平行四边形.
你们能对他们三人的猜想进行证明吗
知识讲解
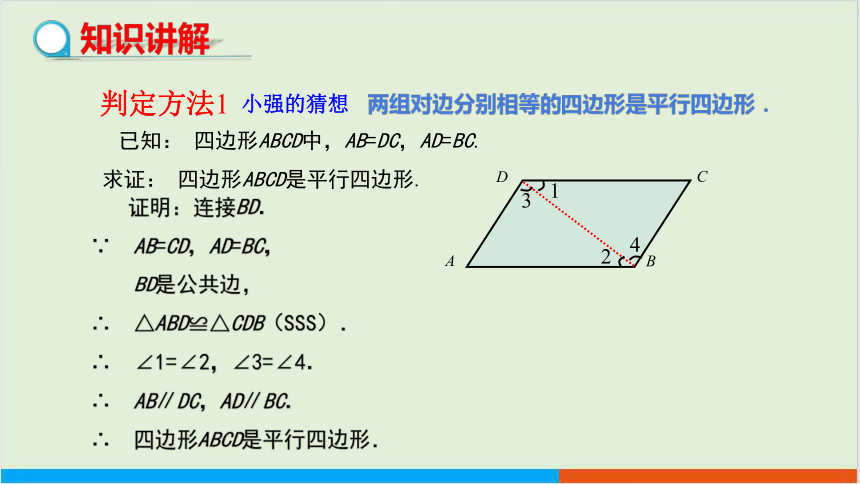
证明:连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB(SSS).
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
已知: 四边形ABCD中,AB=DC,AD=BC.
求证: 四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
判定方法1
小强的猜想
D
A
B
C
1
2
3
4
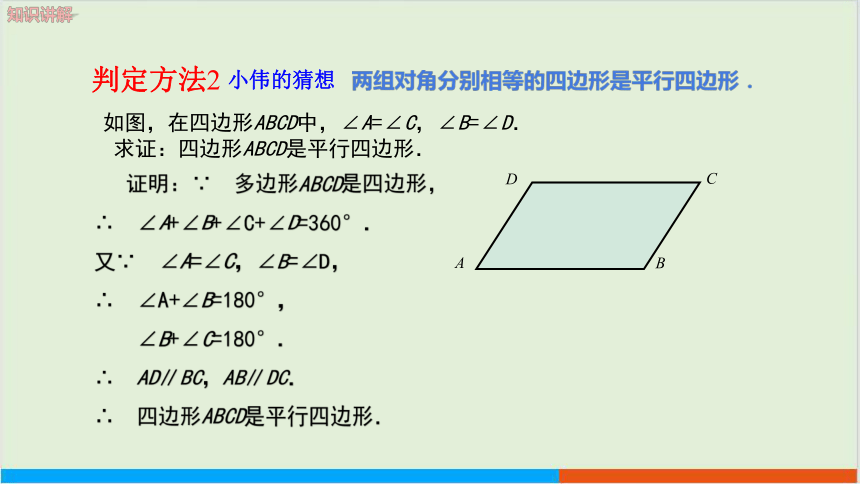
证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形.
判定方法2
小伟的猜想
D
A
B
C
如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
判定方法3
D
A
B
C
O
小丽的猜想
证明:∵ OA=OC,OB=OD,∠1=∠2,
∴ △AOD≌△COB(SAS).
∴ ∠3=∠4.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
1
2
3
4
文字语言 图形语言 几何语言
平行四边形判定方法
判定
方法1
定义法
判定方法2
判定方法3
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是
平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是
平行四边形
∵ ∠ A= ∠ C,
∠ B= ∠ D,
∴四边形ABCD是
平行四边形
∵AO=CO,BO=DO,
∴四边形ABCD是
平行四边形
两组对角分别相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
例1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
D
O
A
B
C
E
F
证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF,
∴AO-AE=CO-CF , 即EO=FO.
又 BO=DO,
∴ 四边形BFDE是平行四边形.
求证:四边形BFDE是平行四边形
随堂训练
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
2.如图,在四边形ABCD中,AC与BD交于点O.
如果AC=8cm,BD=10cm,那么当AO=_____cm,
BO=_____cm时,四边形ABCD是平行四边形.
B
O
D
A
C
4
5
3.如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△ACD中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形ABCD是平行四边形.
4. 如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°;
(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
又∵∠D=∠B=55°,
∴四边形ABCD是平行四边形.
课堂小结
平行四边形的判定(1)
定义法:两组对边分别平行的四边形叫平行四边形.
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
第十八章 平行四边形
18.1.2 平行四边形的判定
第1课时
第十八章 平行四边形
学 习 目 标
通过平行四边形判定定理的猜想与证明过程,体会类比思想及探究图形判定的一般思路.
掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理.(难点)
1
2
新课导入
学行四边形之后,小明回家用细木棒钉制了一个平行四边形.第二天,小明拿着自己动手做的平行四边形向同学们展示.
小红却问:你凭什么确定这四边形就是平行四边形呢
大家议论纷纷……
小强提议说:我们可以度量它的边,如果它的两组对边分别相等,那么它就是一个平行四边形.
小伟提议说:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形.
小丽却说:我们可以度量它的对角线,如果它的对角线互相平分,那么它就是一个平行四边形.
你们能对他们三人的猜想进行证明吗
知识讲解
证明:连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB(SSS).
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
已知: 四边形ABCD中,AB=DC,AD=BC.
求证: 四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
判定方法1
小强的猜想
D
A
B
C
1
2
3
4
证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形.
判定方法2
小伟的猜想
D
A
B
C
如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
判定方法3
D
A
B
C
O
小丽的猜想
证明:∵ OA=OC,OB=OD,∠1=∠2,
∴ △AOD≌△COB(SAS).
∴ ∠3=∠4.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
1
2
3
4
文字语言 图形语言 几何语言
平行四边形判定方法
判定
方法1
定义法
判定方法2
判定方法3
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是
平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是
平行四边形
∵ ∠ A= ∠ C,
∠ B= ∠ D,
∴四边形ABCD是
平行四边形
∵AO=CO,BO=DO,
∴四边形ABCD是
平行四边形
两组对角分别相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
例1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
D
O
A
B
C
E
F
证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF,
∴AO-AE=CO-CF , 即EO=FO.
又 BO=DO,
∴ 四边形BFDE是平行四边形.
求证:四边形BFDE是平行四边形
随堂训练
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
2.如图,在四边形ABCD中,AC与BD交于点O.
如果AC=8cm,BD=10cm,那么当AO=_____cm,
BO=_____cm时,四边形ABCD是平行四边形.
B
O
D
A
C
4
5
3.如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△ACD中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形ABCD是平行四边形.
4. 如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°;
(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
又∵∠D=∠B=55°,
∴四边形ABCD是平行四边形.
课堂小结
平行四边形的判定(1)
定义法:两组对边分别平行的四边形叫平行四边形.
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
