18.1.2 平行四边形的判定(第2课时)教学课件--人教版初中数学八下
文档属性
| 名称 | 18.1.2 平行四边形的判定(第2课时)教学课件--人教版初中数学八下 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:40 | ||
图片预览



文档简介
(共14张PPT)
第十八章 平行四边形
18.1.2 平行四边形的判定
第2课时
第十八章 平行四边形
学 习 目 标
掌握用一组对边平行且相等来判定平行四边形的方法.(重点)
会综合运用平行四边形的判定方法和性质来证明问题.(重点、难点)
1
2
新课导入
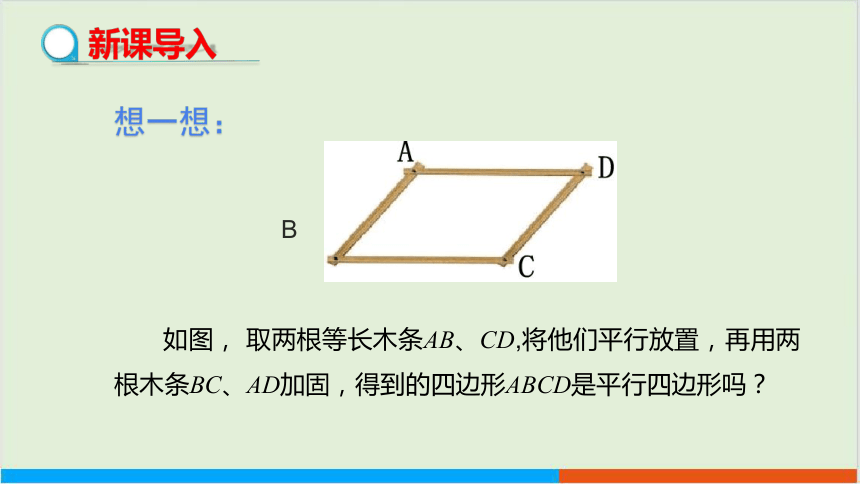
想一想:
B
如图, 取两根等长木条AB、CD,将他们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?
知识讲解
A
B
C
D
1
2
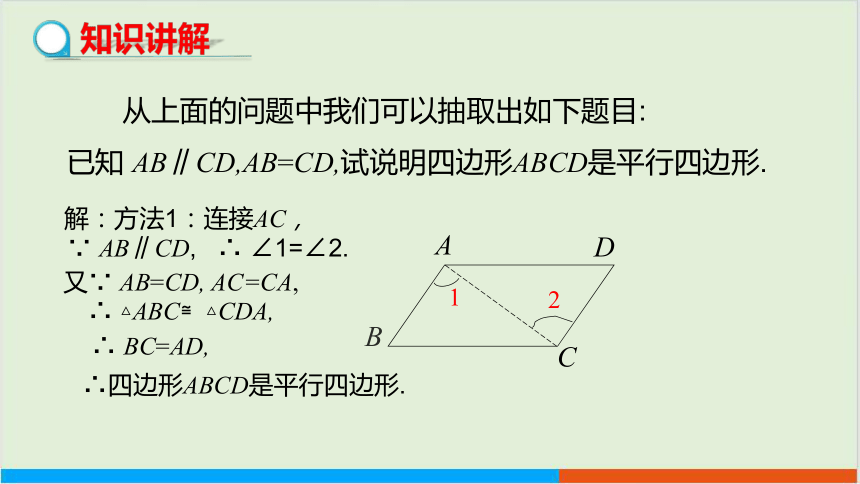
从上面的问题中我们可以抽取出如下题目:
已知 AB∥CD,AB=CD,试说明四边形ABCD是平行四边形.
解:方法1:连接AC,
∵ AB∥CD, ∴ ∠1=∠2.
又∵ AB=CD, AC=CA,
∴ △ABC≌△CDA,
∴ BC=AD,
∴四边形ABCD是平行四边形.
∵AB //CD ,
∴∠1=∠2 .
又 ∵AB =CD ,
AC =CA ,
∴△ABC≌△CDA .
∴∠BCA=∠DAC .
∴AD //BC .
∴四边形ABCD是平行四边形.
方法2:如图,连接 AC.
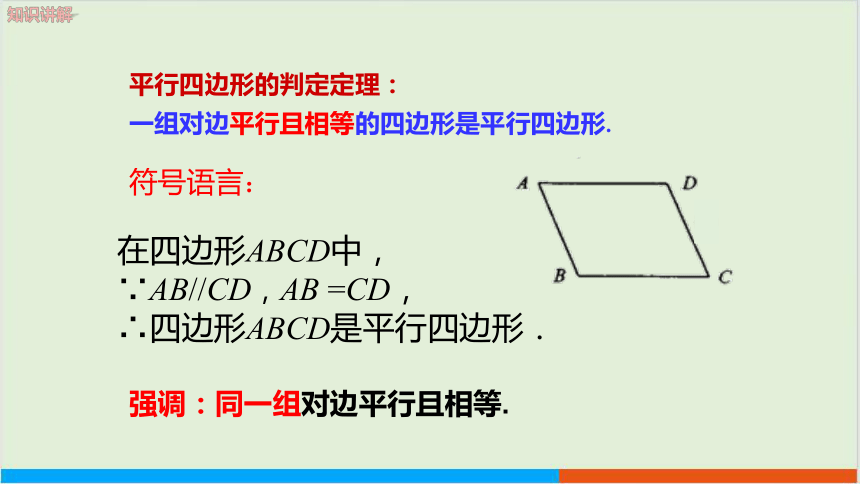
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AB//CD,AB =CD, ∴四边形ABCD是平行四边形.
符号语言:
强调:同一组对边平行且相等.
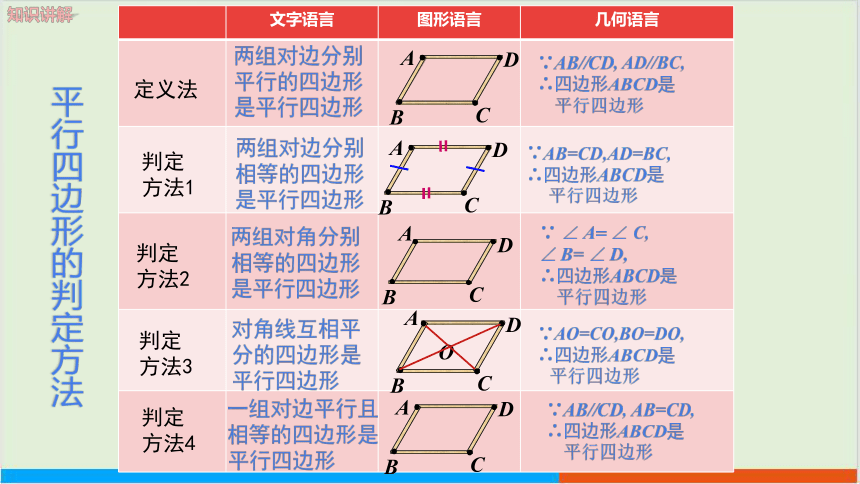
文字语言 图形语言 几何语言
判定
方法1
定义法
判定方法2
判定方法3
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是
平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是
平行四边形
∵ ∠ A= ∠ C,
∠ B= ∠ D,
∴四边形ABCD是
平行四边形
∵AO=CO,BO=DO,
∴四边形ABCD是
平行四边形
两组对角分别相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
判定方法4
一组对边平行且相等的四边形是平行四边形
A
B
C
D
∵AB//CD, AB=CD,
∴四边形ABCD是
平行四边形
平行四边形的判定方法
证明:∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
例 如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
随堂训练
1.四边形ABCD中,已知AB∥CD,再添加一个条件_____________,使四边形ABCD是平行四边形.
AB=CD
提示:本题答案不唯一,如答案也可为AD∥BC.
2.为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了,你能说出其中的道理吗?
解:由一组对边平行且相等的四边形为平行四边形可知,两条直铺的铁轨互相平行.
3.如图, ABCD中,线段EF、GH分别在AB、CD上运动,在运动过程中总是保持EF=GH.
(1)试猜想四边形EFGH的形状,并说明理由.
解:四边形EFGH为平行四边形.
由平行四边形的性质,得AB∥CD,即EF∥GH.又∵EF=GH,
∴四边形EFGH为平行四边形.
(2)若EF= AB,且S ABCD=24,
则S四边形EFGH=____.
8
4.如图,在 ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.求证:四边形AFCE是平行四边形.
证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
又∠AED=∠CFB=90°,∴△AED≌△CFB,
∴AE=CF.
又∵ ∠AEF=∠CFE=90°,
∴ AE∥CF,
∴四边形AFCE是平行四边形.
课堂小结
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
判定一个四边形是平行四边形的方法:
第十八章 平行四边形
18.1.2 平行四边形的判定
第2课时
第十八章 平行四边形
学 习 目 标
掌握用一组对边平行且相等来判定平行四边形的方法.(重点)
会综合运用平行四边形的判定方法和性质来证明问题.(重点、难点)
1
2
新课导入
想一想:
B
如图, 取两根等长木条AB、CD,将他们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?
知识讲解
A
B
C
D
1
2
从上面的问题中我们可以抽取出如下题目:
已知 AB∥CD,AB=CD,试说明四边形ABCD是平行四边形.
解:方法1:连接AC,
∵ AB∥CD, ∴ ∠1=∠2.
又∵ AB=CD, AC=CA,
∴ △ABC≌△CDA,
∴ BC=AD,
∴四边形ABCD是平行四边形.
∵AB //CD ,
∴∠1=∠2 .
又 ∵AB =CD ,
AC =CA ,
∴△ABC≌△CDA .
∴∠BCA=∠DAC .
∴AD //BC .
∴四边形ABCD是平行四边形.
方法2:如图,连接 AC.
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AB//CD,AB =CD, ∴四边形ABCD是平行四边形.
符号语言:
强调:同一组对边平行且相等.
文字语言 图形语言 几何语言
判定
方法1
定义法
判定方法2
判定方法3
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是
平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是
平行四边形
∵ ∠ A= ∠ C,
∠ B= ∠ D,
∴四边形ABCD是
平行四边形
∵AO=CO,BO=DO,
∴四边形ABCD是
平行四边形
两组对角分别相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
判定方法4
一组对边平行且相等的四边形是平行四边形
A
B
C
D
∵AB//CD, AB=CD,
∴四边形ABCD是
平行四边形
平行四边形的判定方法
证明:∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
例 如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
随堂训练
1.四边形ABCD中,已知AB∥CD,再添加一个条件_____________,使四边形ABCD是平行四边形.
AB=CD
提示:本题答案不唯一,如答案也可为AD∥BC.
2.为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了,你能说出其中的道理吗?
解:由一组对边平行且相等的四边形为平行四边形可知,两条直铺的铁轨互相平行.
3.如图, ABCD中,线段EF、GH分别在AB、CD上运动,在运动过程中总是保持EF=GH.
(1)试猜想四边形EFGH的形状,并说明理由.
解:四边形EFGH为平行四边形.
由平行四边形的性质,得AB∥CD,即EF∥GH.又∵EF=GH,
∴四边形EFGH为平行四边形.
(2)若EF= AB,且S ABCD=24,
则S四边形EFGH=____.
8
4.如图,在 ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.求证:四边形AFCE是平行四边形.
证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
又∠AED=∠CFB=90°,∴△AED≌△CFB,
∴AE=CF.
又∵ ∠AEF=∠CFE=90°,
∴ AE∥CF,
∴四边形AFCE是平行四边形.
课堂小结
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
判定一个四边形是平行四边形的方法:
