18.2.1 矩形(第2课时)教学课件--人教版初中数学八下
文档属性
| 名称 | 18.2.1 矩形(第2课时)教学课件--人教版初中数学八下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 332.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:40 | ||
图片预览






文档简介
(共14张PPT)
第十八章 平行四边形
18.2.1 矩形
第2课时
第十八章 平行四边形
学 习 目 标
2
掌握矩形的两个判定定理,能根据不同条件,选取适当的定理进行推理计算. (重点)
1
通过矩形判定定理的猜想与证明过程,渗透类比思想,体会类比学习和图形判定探究的一般思路.
新课导入
一位很有名望的木工师傅,招收了两名徒弟,
一天,师傅有事外出,两徒弟就自已在家练习用
两块四边形的废料各做了一扇矩形式的门,做完
之后,两人都说对方的门不是矩形,而自已的是
矩形。
除了矩形的定义外,有没有
其他判定矩形的方法呢?
问题
你能想一个办法确定
谁做的门是矩形吗?
知识讲解
情境一:李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想:有三个角是直角的四边形是矩形 .
你能证明上述结论吗?
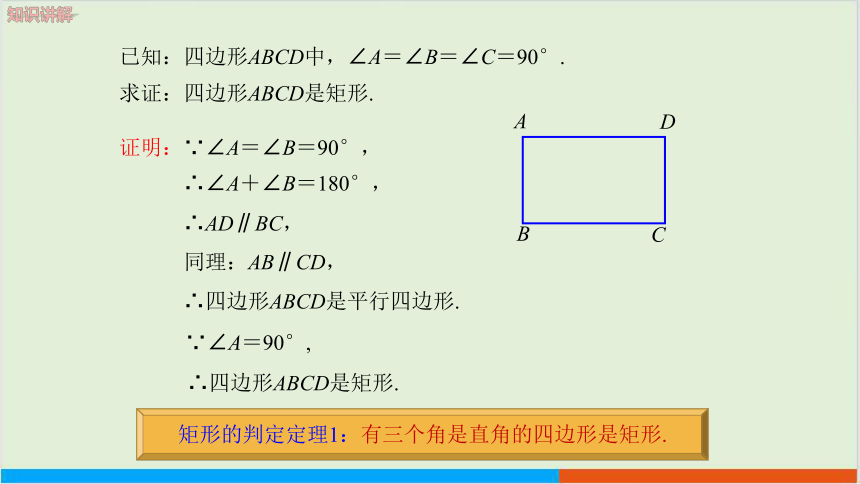
矩形的判定定理1:有三个角是直角的四边形是矩形.
已知:四边形ABCD中,∠A=∠B=∠C=90°.
D
A
B
C
求证:四边形ABCD是矩形.
证明:∵∠A=∠B=90°,
∴∠A+∠B=180°,
∴AD∥BC,
同理:AB∥CD,
∴四边形ABCD是平行四边形.
∵∠A=90°,
∴四边形ABCD是矩形.
情境二:
工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形.
你能证明上述结论吗?
已知:如图,在□ABCD中,AC , DB是它的两条对角线, AC=DB.求证:□ABCD是矩形.
证明:∵ 四边形ABCD是平行四边形,
∴AB = DC, AB∥CD,
∵AB = DC,BC = CB,AC = DB,
∴ △ABC≌ △ DCB ,∴∠ABC = ∠DCB.
∵AB∥CD,∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ □ ABCD是矩形(矩形的定义).
A
B
C
D
矩形的判定定理2:对角线相等的平行四边形是矩形.
A
B
C
D
E
F
G
H
O
例:已知:矩形ABCD的对角线AC、BD相交于O,E、F、G、H分别是AO、BO、CO、DO上的一点,AE=BF=CG=DH.
求证:四边形EFGH是矩形.
证明: ∵四边形ABCD是矩形,
∴ AO=BO=CO=DO.
又∵ AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形.
又∵EO+OG=FO+OH,
即EG=FH,
∴四边形EFGH是矩形.
随堂训练
×
√
×
√
√
1. 现在你能帮两个徒弟解决问题了吗?这两个徒弟下列判定所做的门为矩形的方法中哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形;( )
(3)对角线相等的四边形是矩形;( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)两组对边分别平行,且对角线相等的四边形是矩
形.( )
2、能够判断一个四边形是矩形的条件是( )
A 、对角线相等 B 、对角线垂直
C、对角线互相平分且相等 D、对角线垂直且相等
3、矩形的一组邻边长分别是3cm和4cm,则它的对角线长是 cm.
4、如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、
∠ CAF的角平分线,则四边形ABCD是( )
A 、一般四边形 B、平行四边形
C 、矩形 D 、不能确定
C
5
C
解:
5、在 ABCD中,AC,BD相交于点O,△AOB是等边三角形,求∠ACB的度数.
∵△AOB是等边三角形,
∴OA=OB.
∵四边形ABCD是平行四边形 ,
∴ OA=OC,OB=OD,
在△ABC中 ,∠ABC=90°,
∴ AC=BD,
∴ ABCD是矩形.
∵∠BAC=60°,
∴∠ACB=30°.
6.如图, □ ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形 EFGH为矩形.
证明:在□ ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB、
∠ABC的平分线,
A
B
D
C
H
E
F
G
∴四边形EFGH是矩形.
同理可证∠AED=∠EHG=90°,
∴∠AFB=90°,
∴∠GFE=90°.
∴ ∠BAE+ ∠ABF= ∠DAB+ ∠ABC=90°.
课堂小结
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
运用定理进行计算和证明
矩形的判定
定义
判定定理
第十八章 平行四边形
18.2.1 矩形
第2课时
第十八章 平行四边形
学 习 目 标
2
掌握矩形的两个判定定理,能根据不同条件,选取适当的定理进行推理计算. (重点)
1
通过矩形判定定理的猜想与证明过程,渗透类比思想,体会类比学习和图形判定探究的一般思路.
新课导入
一位很有名望的木工师傅,招收了两名徒弟,
一天,师傅有事外出,两徒弟就自已在家练习用
两块四边形的废料各做了一扇矩形式的门,做完
之后,两人都说对方的门不是矩形,而自已的是
矩形。
除了矩形的定义外,有没有
其他判定矩形的方法呢?
问题
你能想一个办法确定
谁做的门是矩形吗?
知识讲解
情境一:李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想:有三个角是直角的四边形是矩形 .
你能证明上述结论吗?
矩形的判定定理1:有三个角是直角的四边形是矩形.
已知:四边形ABCD中,∠A=∠B=∠C=90°.
D
A
B
C
求证:四边形ABCD是矩形.
证明:∵∠A=∠B=90°,
∴∠A+∠B=180°,
∴AD∥BC,
同理:AB∥CD,
∴四边形ABCD是平行四边形.
∵∠A=90°,
∴四边形ABCD是矩形.
情境二:
工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形.
你能证明上述结论吗?
已知:如图,在□ABCD中,AC , DB是它的两条对角线, AC=DB.求证:□ABCD是矩形.
证明:∵ 四边形ABCD是平行四边形,
∴AB = DC, AB∥CD,
∵AB = DC,BC = CB,AC = DB,
∴ △ABC≌ △ DCB ,∴∠ABC = ∠DCB.
∵AB∥CD,∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ □ ABCD是矩形(矩形的定义).
A
B
C
D
矩形的判定定理2:对角线相等的平行四边形是矩形.
A
B
C
D
E
F
G
H
O
例:已知:矩形ABCD的对角线AC、BD相交于O,E、F、G、H分别是AO、BO、CO、DO上的一点,AE=BF=CG=DH.
求证:四边形EFGH是矩形.
证明: ∵四边形ABCD是矩形,
∴ AO=BO=CO=DO.
又∵ AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形.
又∵EO+OG=FO+OH,
即EG=FH,
∴四边形EFGH是矩形.
随堂训练
×
√
×
√
√
1. 现在你能帮两个徒弟解决问题了吗?这两个徒弟下列判定所做的门为矩形的方法中哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形;( )
(3)对角线相等的四边形是矩形;( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)两组对边分别平行,且对角线相等的四边形是矩
形.( )
2、能够判断一个四边形是矩形的条件是( )
A 、对角线相等 B 、对角线垂直
C、对角线互相平分且相等 D、对角线垂直且相等
3、矩形的一组邻边长分别是3cm和4cm,则它的对角线长是 cm.
4、如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、
∠ CAF的角平分线,则四边形ABCD是( )
A 、一般四边形 B、平行四边形
C 、矩形 D 、不能确定
C
5
C
解:
5、在 ABCD中,AC,BD相交于点O,△AOB是等边三角形,求∠ACB的度数.
∵△AOB是等边三角形,
∴OA=OB.
∵四边形ABCD是平行四边形 ,
∴ OA=OC,OB=OD,
在△ABC中 ,∠ABC=90°,
∴ AC=BD,
∴ ABCD是矩形.
∵∠BAC=60°,
∴∠ACB=30°.
6.如图, □ ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形 EFGH为矩形.
证明:在□ ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB、
∠ABC的平分线,
A
B
D
C
H
E
F
G
∴四边形EFGH是矩形.
同理可证∠AED=∠EHG=90°,
∴∠AFB=90°,
∴∠GFE=90°.
∴ ∠BAE+ ∠ABF= ∠DAB+ ∠ABC=90°.
课堂小结
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
运用定理进行计算和证明
矩形的判定
定义
判定定理
