18.2.2 菱形(第1课时)教学课件--人教版初中数学八下
文档属性
| 名称 | 18.2.2 菱形(第1课时)教学课件--人教版初中数学八下 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:40 | ||
图片预览




文档简介
(共19张PPT)
第十八章 平行四边形
18.2.2 菱形
第1课时
第十八章 平行四边形
学 习 目 标
2
探索并证明菱形的性质定理.(重点)
1
应用菱形的性质定理解决相关计算或证明问题.(难点)
知识讲解
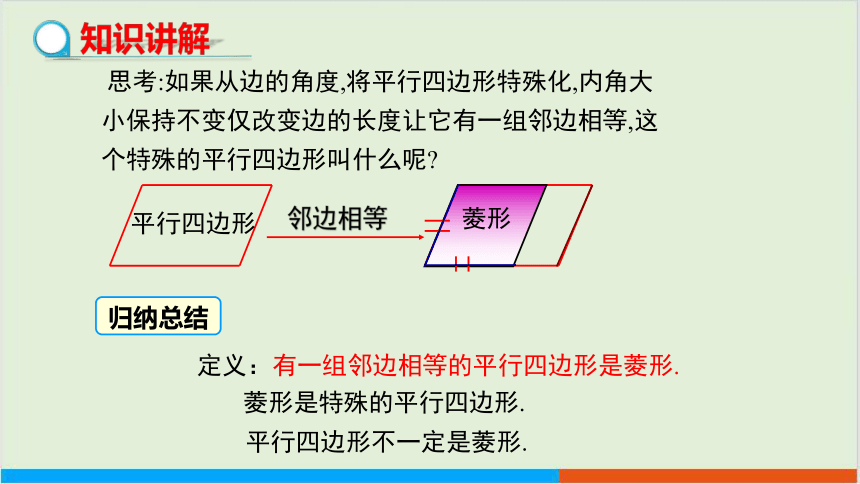
思考:如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢
平行四边形
定义:有一组邻边相等的平行四边形是菱形.
菱形
邻边相等
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
归纳总结
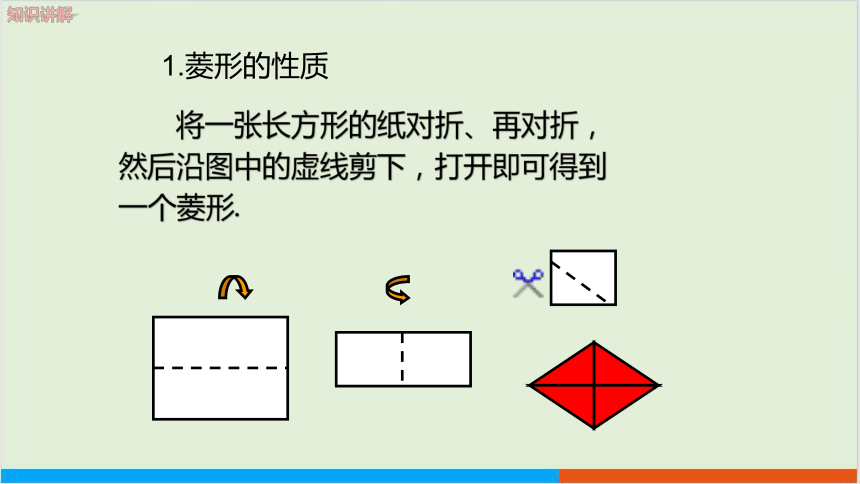
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可得到一个菱形.
1.菱形的性质
画出菱形的两条折痕,并通过折叠手中的图形回答以下问题:
1.菱形是轴对称图形吗?
2.菱形有几条对称轴?
3.对称轴之间有什么关系?
4.你能看出图中哪些线段和角相等?
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
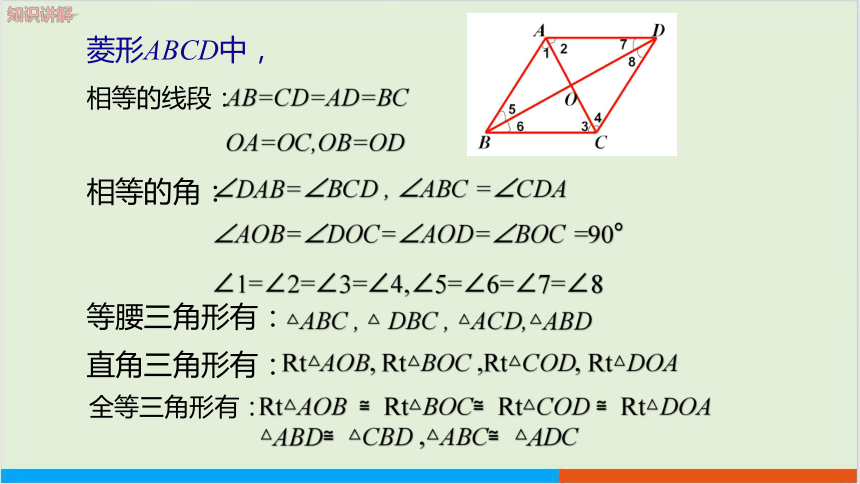
菱形ABCD中,
AB=CD=AD=BC
OA=OC,OB=OD
∠DAB=∠BCD , ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4,∠5=∠6=∠7=∠8
△ABC , △ DBC , △ACD,△ABD
Rt△AOB, Rt△BOC ,Rt△COD, Rt△DOA
Rt△AOB ≌Rt△BOC≌Rt△COD ≌Rt△DOA
△ABD≌△CBD ,△ABC≌△ADC
菱形是特殊的平行四边形,具有平行四边形的所有性质.
由此我们可以得到菱形的性质:
菱形是轴对称图形, 对称轴有两条,是菱形两条对角线所在的直线.
问题:猜想菱形的四条边在数量上有什么关系 菱形的两条
对角线有什么关系
猜想1 菱形的四条边都相等.
猜想2 菱形的两条对角线互相垂直,并且每一条对
角线平分一组对角.
已知:如图,四边形ABCD是菱形.
求证:(1)AB = BC = CD =AD;
(2)AC⊥BD;
∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
证明:(1)∵四边形ABCD是菱形,
∴AB=AD.
又∵AB = CD,AD = BC,
∴AB = BC = CD =AD.
A
B
C
O
D
证一证
(2)∵AB = AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB = OD .
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
例1 如图,在菱形ABCD中,CE⊥AB于点E,CF⊥AD于点F,求证:AE=AF.
证明:连接AC.
∵四边形ABCD是菱形,
∴AC平分∠BAD,
即∠BAC=∠DAC.
∵CE⊥AB,CF⊥AD,
∴∠AEC=∠AFC=90°.
又∵AC=AC,
∴△ACE≌△ACF.
∴AE=AF.
问题1 菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积吗
A
B
C
D
思考 前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢
能.过点A作AE⊥BC于点E,
则S菱形ABCD=底×高
=BC·AE.
E
2.菱形的面积
问题2 如图,四边形ABCD是菱形,对角线AC,BD交于点O,试用对角线表示出菱形ABCD的面积.
A
B
C
D
O
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC +S△ADC
= AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
你有什么发现?
菱形的面积 = 底×高 = 对角线乘积的一半
例2 如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,OA=5,OB=12,
∴S△AOB= OA·OB= ×5×12=30,
∴S菱形ABCD=4S△AOB=4×30=120.
∵
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,
∴13h=120,得h= .
随堂训练
1.如图,在菱形ABCD中,已知∠A=60°,AB=
5,则△ABD的周长是 ( )
A.10 B.12 C.15 D.20
C
2.如图,菱形ABCD的周长为48cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
第1题图
第2题图
6cm
3.如图,已知菱形的两条对角线长分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm C.5cm D.9.6cm
B
4.如图,四边形ABCD是边长为13cm的菱形,其中对
角线BD长10cm.
求:(1)对角线AC的长度;
(2)菱形ABCD的面积.
解:(1)
∵四边形ABCD是菱形,
∴∠AED=90°,
(2)菱形ABCD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
5.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.
解:(1)∵四边形ABCD是菱形,∴AC⊥BD.
在RT△OCD中,由勾股定理得OC=4cm.
(2)∵CE∥DB,BE∥AC,
∴四边形OBEC为平行四边形.
又∵AC⊥BD,即∠COB=90°,
∴平行四边形OBEC为矩形.
∵OB=OD=3cm,
∴S矩形OBEC=OB·OC=4×3=12(cm2).
课堂小结
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
第十八章 平行四边形
18.2.2 菱形
第1课时
第十八章 平行四边形
学 习 目 标
2
探索并证明菱形的性质定理.(重点)
1
应用菱形的性质定理解决相关计算或证明问题.(难点)
知识讲解
思考:如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢
平行四边形
定义:有一组邻边相等的平行四边形是菱形.
菱形
邻边相等
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
归纳总结
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可得到一个菱形.
1.菱形的性质
画出菱形的两条折痕,并通过折叠手中的图形回答以下问题:
1.菱形是轴对称图形吗?
2.菱形有几条对称轴?
3.对称轴之间有什么关系?
4.你能看出图中哪些线段和角相等?
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
菱形ABCD中,
AB=CD=AD=BC
OA=OC,OB=OD
∠DAB=∠BCD , ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4,∠5=∠6=∠7=∠8
△ABC , △ DBC , △ACD,△ABD
Rt△AOB, Rt△BOC ,Rt△COD, Rt△DOA
Rt△AOB ≌Rt△BOC≌Rt△COD ≌Rt△DOA
△ABD≌△CBD ,△ABC≌△ADC
菱形是特殊的平行四边形,具有平行四边形的所有性质.
由此我们可以得到菱形的性质:
菱形是轴对称图形, 对称轴有两条,是菱形两条对角线所在的直线.
问题:猜想菱形的四条边在数量上有什么关系 菱形的两条
对角线有什么关系
猜想1 菱形的四条边都相等.
猜想2 菱形的两条对角线互相垂直,并且每一条对
角线平分一组对角.
已知:如图,四边形ABCD是菱形.
求证:(1)AB = BC = CD =AD;
(2)AC⊥BD;
∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
证明:(1)∵四边形ABCD是菱形,
∴AB=AD.
又∵AB = CD,AD = BC,
∴AB = BC = CD =AD.
A
B
C
O
D
证一证
(2)∵AB = AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB = OD .
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
例1 如图,在菱形ABCD中,CE⊥AB于点E,CF⊥AD于点F,求证:AE=AF.
证明:连接AC.
∵四边形ABCD是菱形,
∴AC平分∠BAD,
即∠BAC=∠DAC.
∵CE⊥AB,CF⊥AD,
∴∠AEC=∠AFC=90°.
又∵AC=AC,
∴△ACE≌△ACF.
∴AE=AF.
问题1 菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积吗
A
B
C
D
思考 前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢
能.过点A作AE⊥BC于点E,
则S菱形ABCD=底×高
=BC·AE.
E
2.菱形的面积
问题2 如图,四边形ABCD是菱形,对角线AC,BD交于点O,试用对角线表示出菱形ABCD的面积.
A
B
C
D
O
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC +S△ADC
= AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
你有什么发现?
菱形的面积 = 底×高 = 对角线乘积的一半
例2 如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,OA=5,OB=12,
∴S△AOB= OA·OB= ×5×12=30,
∴S菱形ABCD=4S△AOB=4×30=120.
∵
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,
∴13h=120,得h= .
随堂训练
1.如图,在菱形ABCD中,已知∠A=60°,AB=
5,则△ABD的周长是 ( )
A.10 B.12 C.15 D.20
C
2.如图,菱形ABCD的周长为48cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
第1题图
第2题图
6cm
3.如图,已知菱形的两条对角线长分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm C.5cm D.9.6cm
B
4.如图,四边形ABCD是边长为13cm的菱形,其中对
角线BD长10cm.
求:(1)对角线AC的长度;
(2)菱形ABCD的面积.
解:(1)
∵四边形ABCD是菱形,
∴∠AED=90°,
(2)菱形ABCD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
5.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.
解:(1)∵四边形ABCD是菱形,∴AC⊥BD.
在RT△OCD中,由勾股定理得OC=4cm.
(2)∵CE∥DB,BE∥AC,
∴四边形OBEC为平行四边形.
又∵AC⊥BD,即∠COB=90°,
∴平行四边形OBEC为矩形.
∵OB=OD=3cm,
∴S矩形OBEC=OB·OC=4×3=12(cm2).
课堂小结
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
