18.2.3 正方形教学课件--人教版初中数学八下
文档属性
| 名称 | 18.2.3 正方形教学课件--人教版初中数学八下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:40 | ||
图片预览


文档简介
(共14张PPT)
第十八章 平行四边形
18.2.3 正方形
第十八章 平行四边形
学 习 目 标
2
掌握正方形的定义、性质,并能灵活运用.(重点)
1
理解正方形与平行四边形、矩形、菱形的联系并归纳出正方形的判定定理.(难点)
知识讲解
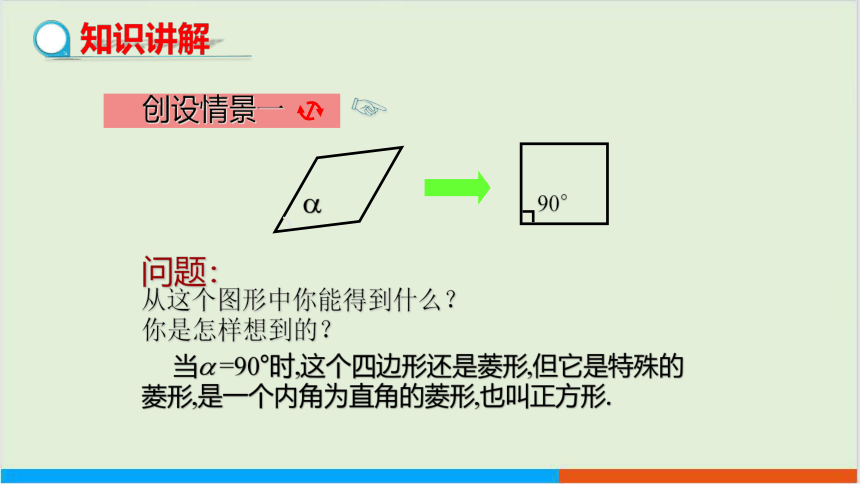
创设情景一
问题:
从这个图形中你能得到什么?
你是怎样想到的?
┓
90°
当 =90°时,这个四边形还是菱形,但它是特殊的菱形,是一个内角为直角的菱形,也叫正方形.
问题:
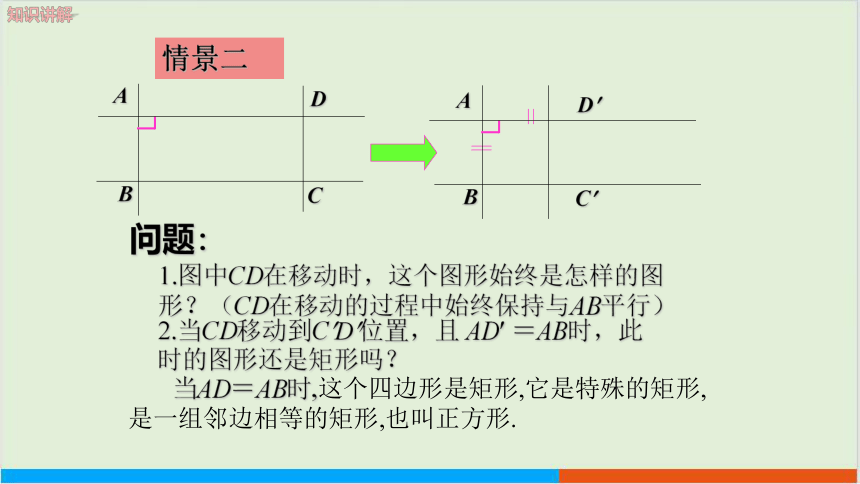
情景二
1.图中CD在移动时,这个图形始终是怎样的图形?(CD在移动的过程中始终保持与AB平行)
2.当CD移动到C D 位置,且 AD =AB时,此
时的图形还是矩形吗?
A
B
C
D
A
B
C
D
当AD=AB时,这个四边形是矩形,它是特殊的矩形,是一组邻边相等的矩形,也叫正方形.
矩 形
〃
〃
正方形
邻边
相等
〃
〃
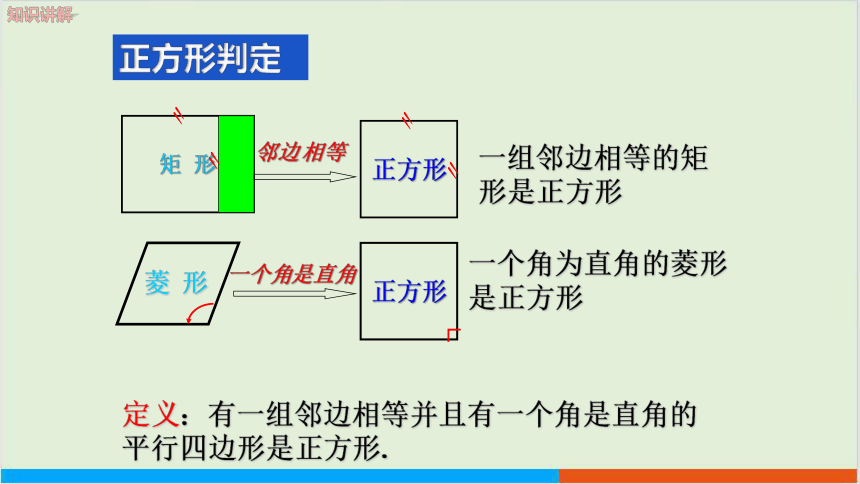
一组邻边相等的矩形是正方形
菱 形
一个角
是直角
正方形
∟
一个角为直角的菱形是正方形
定义:有一组邻边相等并且有一个角是直角的平行四边形是正方形.
正方形判定
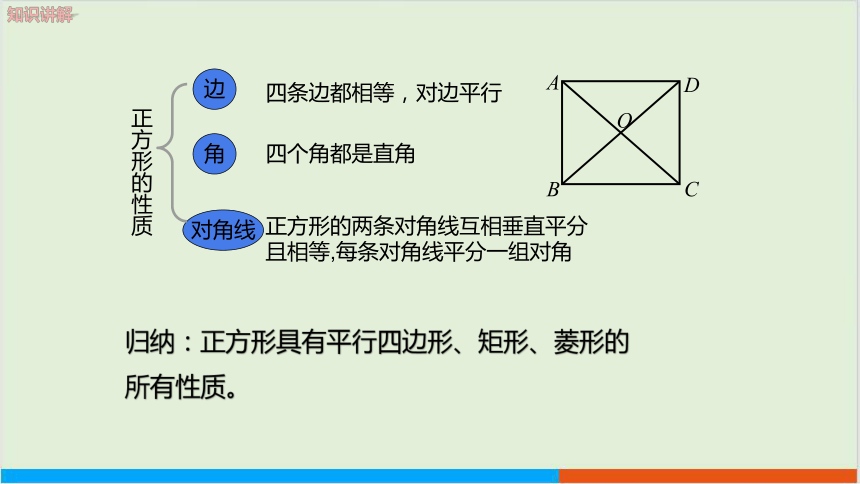
正方形的两条对角线互相垂直平分且相等,每条对角线平分一组对角
四条边都相等,对边平行
四个角都是直角
边
对角线
角
正方形的性质
O
A
B
C
D
归纳:正方形具有平行四边形、矩形、菱形的所有性质。
平行四边形
矩形
菱形
正
方
形
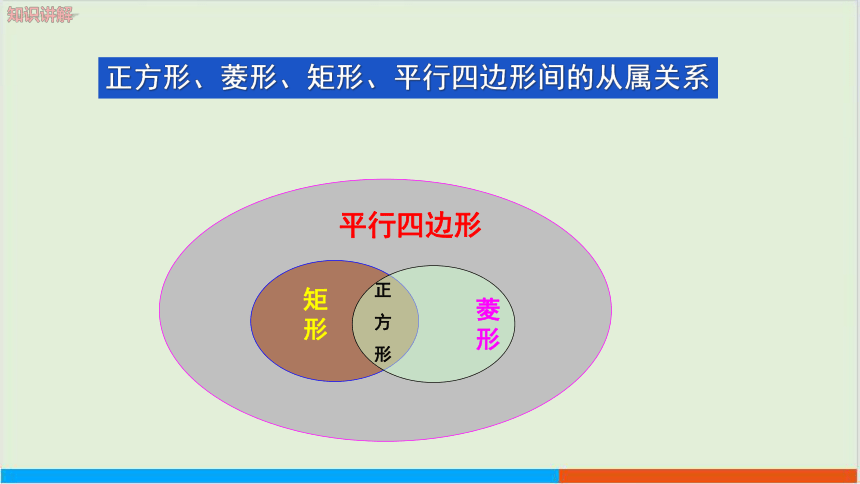
正方形、菱形、矩形、平行四边形间的从属关系
E
A
B
C
D
F
N
M
例:如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论。
解:四边形EFMN是正方形。
理由:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°。
又∵AE=BF=CM=DN,∴BE=CF=DM=AN,
∴Rt△EBF≌ Rt△FCM ≌ Rt△MDN ≌ Rt△NAE(SAS),
∴EF=FM=MN=EN,∠AEN=∠EFB。
∵∠EFB+∠BEF=90°,
∴∠NEF=90°,
∴四边形EFMN是正方形。
随堂训练
1.如图,已知E点在正方形ABCD的BC边的延长线上,且CE=AC,AE与CD相交
于点F,则∠AFC=________.
2.已知正方形的面积为9cm,它的周长为 _____.
3.已知在平行四边形ABCD中,∠A=90°,如果添加一个条件,可使该四边形是正方形,那么这个条件可以是( )
A.∠D=90° B.AB=CD C. AD=BC D. BC=CD
112.5 °
D
12cm
112.5 °
4.已知正方形ABCD中,AC=10,P是AB上一点,
PE⊥AC于E,PF⊥BD于F,则PE+PF=____.
5
30°
5.以正方形ABCD的边DC向外作等边△DCE,
则∠AEB=_____.
P
A
B
C
D
E
F
O
E
A
B
C
D
6.正方形具有而矩形不一定具有的性质是( )
A、四个角相等
B、对角线互相垂直
C、对角互补
D、对角线相等
7.正方形具有而菱形不一定具有的性质( )
A、四条边相等
B、对角线互相垂直平分
C、对角线平分一组对角
D、对角线相等
B
D
8.根据图形所具有的性质,在下表中相应的空格里打“ √ ”
√ √ √ √
√ √
√ √
√ √ √ √
√ √
√ √
√ √
课堂小结
边 角 对角线
平行四边形 对边平行且相等 对角相等 对角线互相平分
矩形 对边平行且相等 四个角都是直角 对角线互相平分、相等
菱形 对边平行, 四条边相等 对角相等 对角线互相垂直、平分,. 每一条对角线平分一组对角
正方形 对边平行, 四条边相等 四个角都是直角 对角线互相垂直、平分且相等, 每一条对角线平分一组对角
第十八章 平行四边形
18.2.3 正方形
第十八章 平行四边形
学 习 目 标
2
掌握正方形的定义、性质,并能灵活运用.(重点)
1
理解正方形与平行四边形、矩形、菱形的联系并归纳出正方形的判定定理.(难点)
知识讲解
创设情景一
问题:
从这个图形中你能得到什么?
你是怎样想到的?
┓
90°
当 =90°时,这个四边形还是菱形,但它是特殊的菱形,是一个内角为直角的菱形,也叫正方形.
问题:
情景二
1.图中CD在移动时,这个图形始终是怎样的图形?(CD在移动的过程中始终保持与AB平行)
2.当CD移动到C D 位置,且 AD =AB时,此
时的图形还是矩形吗?
A
B
C
D
A
B
C
D
当AD=AB时,这个四边形是矩形,它是特殊的矩形,是一组邻边相等的矩形,也叫正方形.
矩 形
〃
〃
正方形
邻边
相等
〃
〃
一组邻边相等的矩形是正方形
菱 形
一个角
是直角
正方形
∟
一个角为直角的菱形是正方形
定义:有一组邻边相等并且有一个角是直角的平行四边形是正方形.
正方形判定
正方形的两条对角线互相垂直平分且相等,每条对角线平分一组对角
四条边都相等,对边平行
四个角都是直角
边
对角线
角
正方形的性质
O
A
B
C
D
归纳:正方形具有平行四边形、矩形、菱形的所有性质。
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形间的从属关系
E
A
B
C
D
F
N
M
例:如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论。
解:四边形EFMN是正方形。
理由:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°。
又∵AE=BF=CM=DN,∴BE=CF=DM=AN,
∴Rt△EBF≌ Rt△FCM ≌ Rt△MDN ≌ Rt△NAE(SAS),
∴EF=FM=MN=EN,∠AEN=∠EFB。
∵∠EFB+∠BEF=90°,
∴∠NEF=90°,
∴四边形EFMN是正方形。
随堂训练
1.如图,已知E点在正方形ABCD的BC边的延长线上,且CE=AC,AE与CD相交
于点F,则∠AFC=________.
2.已知正方形的面积为9cm,它的周长为 _____.
3.已知在平行四边形ABCD中,∠A=90°,如果添加一个条件,可使该四边形是正方形,那么这个条件可以是( )
A.∠D=90° B.AB=CD C. AD=BC D. BC=CD
112.5 °
D
12cm
112.5 °
4.已知正方形ABCD中,AC=10,P是AB上一点,
PE⊥AC于E,PF⊥BD于F,则PE+PF=____.
5
30°
5.以正方形ABCD的边DC向外作等边△DCE,
则∠AEB=_____.
P
A
B
C
D
E
F
O
E
A
B
C
D
6.正方形具有而矩形不一定具有的性质是( )
A、四个角相等
B、对角线互相垂直
C、对角互补
D、对角线相等
7.正方形具有而菱形不一定具有的性质( )
A、四条边相等
B、对角线互相垂直平分
C、对角线平分一组对角
D、对角线相等
B
D
8.根据图形所具有的性质,在下表中相应的空格里打“ √ ”
√ √ √ √
√ √
√ √
√ √ √ √
√ √
√ √
√ √
课堂小结
边 角 对角线
平行四边形 对边平行且相等 对角相等 对角线互相平分
矩形 对边平行且相等 四个角都是直角 对角线互相平分、相等
菱形 对边平行, 四条边相等 对角相等 对角线互相垂直、平分,. 每一条对角线平分一组对角
正方形 对边平行, 四条边相等 四个角都是直角 对角线互相垂直、平分且相等, 每一条对角线平分一组对角
