19.2.3 一次函数与方程、不等式教学课件--人教版初中数学八下
文档属性
| 名称 | 19.2.3 一次函数与方程、不等式教学课件--人教版初中数学八下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:40 | ||
图片预览





文档简介
(共27张PPT)
第十九章 一次函数
19.2 一次函数
19.2.3 一次函数与方程、不等式
学 习 目 标
1
2
认识一次函数与一元(二元)一次方程(组)、
一元一次不等式之间的联系.(重点、难点)
会用函数观点解释方程和不等式及其解(解集)
的意义.
新课导入
思考:
问题①:解方程2x+20=0;
问题②:当 x为何值时,函数y=2x+20的值为0?
问题③:画出函数y=2x+20的图象,并确定它与x 轴的交点坐标;
问题④:问题① ②有何关系? ① ③呢?
问题⑤ : 能从函数的角度来解一元一次方程 2x+20=0吗?
知识讲解
一次函数与一元一次方程
3
2
1
2
1
-2
O
x
y
-1
-1
3
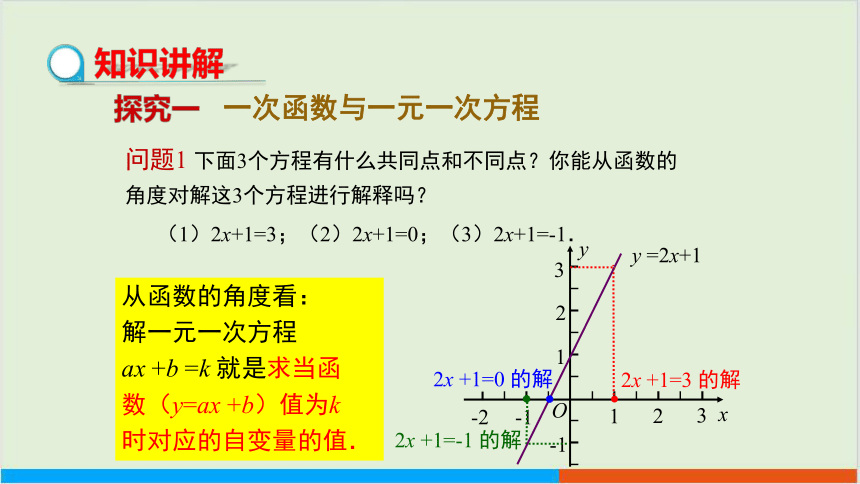
问题1 下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
从函数的角度看:
解一元一次方程
ax +b =k 就是求当函
数(y=ax +b)值为k
时对应的自变量的值.
2x +1=3 的解
y =2x+1
2x +1=0 的解
2x +1=-1 的解
探究一
练一练
2、如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
A.x=2 B.x=0
C.x=-1 D.x=-3
D
1、解方程2x+3=5就是求当y= 时,函数y=2x+3的自变量x的取值.
(0,2)
5
(-3,0)
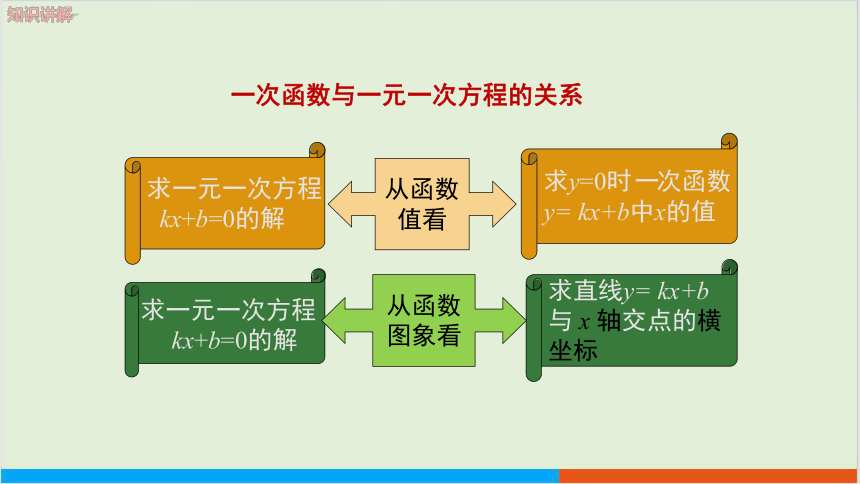
求一元一次方程
kx+b=0的解
一次函数与一元一次方程的关系
求y=0时一次函数
y= kx+b中x的值
从函数
值看
求一元一次方程
kx+b=0的解
求直线y= kx+b
与 x 轴交点的横
坐标
从函数
图象看
探究二
一次函数与一元一次不等式
问题2 观察下面这几个不等式:
你能类比一次函数和一元一次方程的关系,试着从函数的角度解一元一次不等式吗?
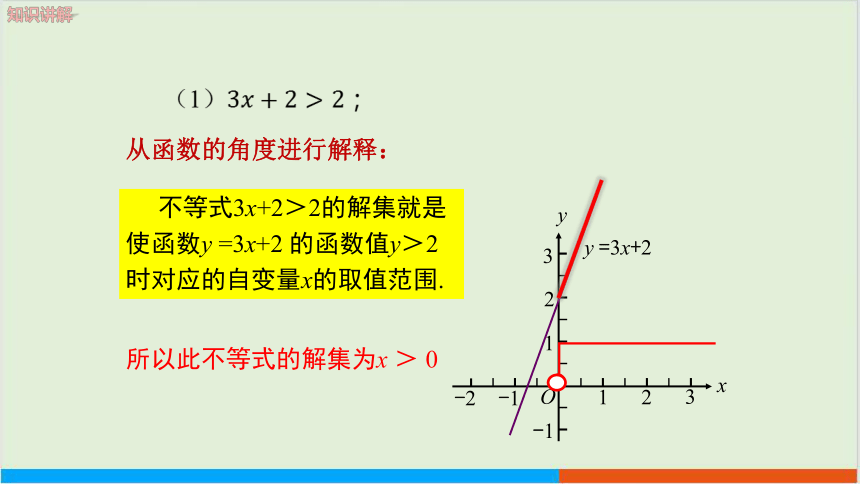
(1); (2); (3).
不等式3x+2>2的解集就是
使函数y =3x+2 的函数值y>2
时对应的自变量x的取值范围.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
从函数的角度进行解释:
所以此不等式的解集为x > 0
(1)
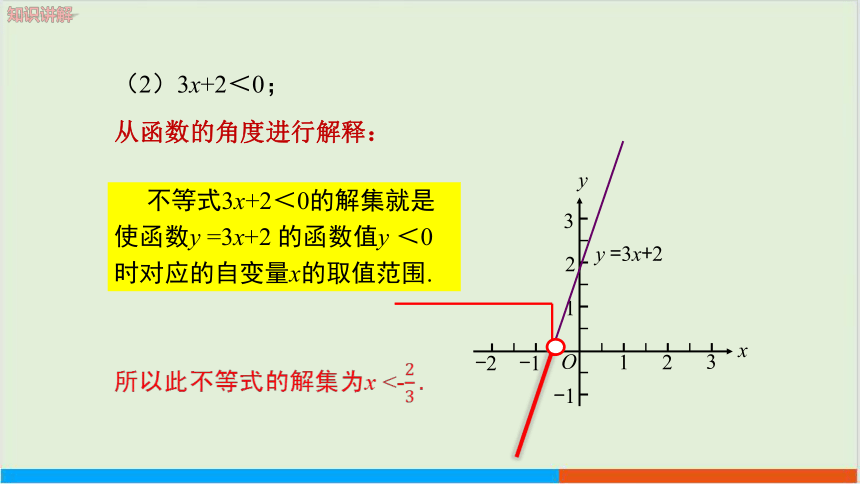
(2)3x+2<0;
不等式3x+2<0的解集就是
使函数y =3x+2 的函数值y <0
时对应的自变量x的取值范围.
所以此不等式的解集为x <-
从函数的角度进行解释:
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
不等式3x+2<-1的解集就是
使函数y =3x+2 的函数值y<-1
时对应的自变量x的取值范围.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
所以此不等式的解集为x<-1
(3)3x+2<-1.
从函数的角度进行解释:
能把你得到的结论推广到一般情形吗?
不等式ax+b>c的解集就是使函数y =ax+b 的函数值大于c的对应的自变量取值范围;
不等式ax+b<c的解集就是使函数y =ax+b 的函数值小于c的对应的自变量取值范围.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
y =2
y =0
y =-1
从函数的角度看:
例1 画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3
解:作出函数y=-3x+6的图象,如图所示,图象与x轴交于点B(2,0).
x
O
B(2,0)
A(0,6)
y
解:(1)由图象可知,不等式
-3x+6>0 的解集是图象位于 x轴上方的x的取值范围,即x<2;
不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
x
O
B(2,0)
A(0,6)
3
1
(1,3)
y
(2)由图象可知,当x>1时,y<3.
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3
求kx+b>0(或<0)
(k≠0)的解集
y=kx+b的值
大于(或小于)0时,
x的取值范围
从函数
值看
求kx+b>0(或<0)
(k≠0)的解集
直线y=kx+b在x
轴上方(或下方)
的x取值范围
从函数
图象看
一次函数与一元一次不等式的关系
探究三
一次函数与二元一次方程组
例2 1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
(1)用式子分别表示两个气球所在位置的海拔 y(m)
关于上升时间 x(min)的函数关系;
1号气球:y =x+5;
2号气球:y =0.5x+15.
思考1:一次函数与二元一次方程从数的角度看有什么关系?
一次函数
y =0.5x+15
二元一次方程
y -0.5x =15
从方程角度看
从函数角度看
由函数图象的定义可知:
直线上每个点的坐标(x , y)都是这个二元一次方程的解.
思考2:从形的角度看,一次函数与二元一次方程有什么关系?
二元一次方程组的解就是相应的 两个一次函数图象的交点坐标.
思考3:从形的角度看,二元一次方程组与一次函数有什么关系?
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
从数的角度看:
就是求自变量为何值时,两个一次函数 y =x+5,y =0.5x+15 的函数值相等,并求出函数值.
解方程组
y =x+5,
y =0.5x+15
(2)在某时刻两个气球能否位于同一高度?如果能,
这时气球上升了多长时间?位于什么高度?
解方程组
y =x+5,
y =0.5x+15,
∴当上升20 min 时,两个气球都位于海拔25 m的高度.
A(20,25)
30
25
20
15
10
5
y =x+5
y =0.5x+15
O
y
观察图象,两条直线的交点坐标是(20,25).
∴当上升20 min 时,两个气球都位于海拔25 m的高度.
从形的角度看:
一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
方程组的解 对应两条直线交点的坐标.
总结
随堂训练
1、一次函数y=ax+b的图象如图所示,则不等式ax+b≥0的解集是( )
A.x≥2 B.x≤2
C.x≥4 D.x≤4
B
2、小亮用作图象的方法解二元一次方程组时,在
同一直角坐标系内作出了相应的两条直线l1、l2
如图 ,他解的这个方程组是( )
D
点拨:由图象知l1、l2 的 x 的系数都应为负数,排除 A、
C.又 l1、l2的交点为(2,-2),代入验证可知只有 D 符合.
3、如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式-2<kx+b<1的 解集__________ .
-1<x<2
2
1
-2
-1
4、当x 时,直线y=-x+2上的点在x轴的下方.
x
o
y
2
2
5、直线=-x+m和=2x+n的交点如图,则不等式-x+m<2x+n的解集是 .
x
o
y
2
1
>2
x<1
y1=-x+m
y2=2x+n
课堂小结
一次函数与方程、不等式
解一元一次方程 对应一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标
解一元一次不等式 对应一次函数的函数值大(小)于0时,求自变量的取值范围,即在x轴上方(或下方)的图象所对应的x的取值范围
解二元一次方程组 求对应两条直线交点的坐标
第十九章 一次函数
19.2 一次函数
19.2.3 一次函数与方程、不等式
学 习 目 标
1
2
认识一次函数与一元(二元)一次方程(组)、
一元一次不等式之间的联系.(重点、难点)
会用函数观点解释方程和不等式及其解(解集)
的意义.
新课导入
思考:
问题①:解方程2x+20=0;
问题②:当 x为何值时,函数y=2x+20的值为0?
问题③:画出函数y=2x+20的图象,并确定它与x 轴的交点坐标;
问题④:问题① ②有何关系? ① ③呢?
问题⑤ : 能从函数的角度来解一元一次方程 2x+20=0吗?
知识讲解
一次函数与一元一次方程
3
2
1
2
1
-2
O
x
y
-1
-1
3
问题1 下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
从函数的角度看:
解一元一次方程
ax +b =k 就是求当函
数(y=ax +b)值为k
时对应的自变量的值.
2x +1=3 的解
y =2x+1
2x +1=0 的解
2x +1=-1 的解
探究一
练一练
2、如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
A.x=2 B.x=0
C.x=-1 D.x=-3
D
1、解方程2x+3=5就是求当y= 时,函数y=2x+3的自变量x的取值.
(0,2)
5
(-3,0)
求一元一次方程
kx+b=0的解
一次函数与一元一次方程的关系
求y=0时一次函数
y= kx+b中x的值
从函数
值看
求一元一次方程
kx+b=0的解
求直线y= kx+b
与 x 轴交点的横
坐标
从函数
图象看
探究二
一次函数与一元一次不等式
问题2 观察下面这几个不等式:
你能类比一次函数和一元一次方程的关系,试着从函数的角度解一元一次不等式吗?
(1); (2); (3).
不等式3x+2>2的解集就是
使函数y =3x+2 的函数值y>2
时对应的自变量x的取值范围.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
从函数的角度进行解释:
所以此不等式的解集为x > 0
(1)
(2)3x+2<0;
不等式3x+2<0的解集就是
使函数y =3x+2 的函数值y <0
时对应的自变量x的取值范围.
所以此不等式的解集为x <-
从函数的角度进行解释:
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
不等式3x+2<-1的解集就是
使函数y =3x+2 的函数值y<-1
时对应的自变量x的取值范围.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
所以此不等式的解集为x<-1
(3)3x+2<-1.
从函数的角度进行解释:
能把你得到的结论推广到一般情形吗?
不等式ax+b>c的解集就是使函数y =ax+b 的函数值大于c的对应的自变量取值范围;
不等式ax+b<c的解集就是使函数y =ax+b 的函数值小于c的对应的自变量取值范围.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
y =2
y =0
y =-1
从函数的角度看:
例1 画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3
解:作出函数y=-3x+6的图象,如图所示,图象与x轴交于点B(2,0).
x
O
B(2,0)
A(0,6)
y
解:(1)由图象可知,不等式
-3x+6>0 的解集是图象位于 x轴上方的x的取值范围,即x<2;
不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
x
O
B(2,0)
A(0,6)
3
1
(1,3)
y
(2)由图象可知,当x>1时,y<3.
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3
求kx+b>0(或<0)
(k≠0)的解集
y=kx+b的值
大于(或小于)0时,
x的取值范围
从函数
值看
求kx+b>0(或<0)
(k≠0)的解集
直线y=kx+b在x
轴上方(或下方)
的x取值范围
从函数
图象看
一次函数与一元一次不等式的关系
探究三
一次函数与二元一次方程组
例2 1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
(1)用式子分别表示两个气球所在位置的海拔 y(m)
关于上升时间 x(min)的函数关系;
1号气球:y =x+5;
2号气球:y =0.5x+15.
思考1:一次函数与二元一次方程从数的角度看有什么关系?
一次函数
y =0.5x+15
二元一次方程
y -0.5x =15
从方程角度看
从函数角度看
由函数图象的定义可知:
直线上每个点的坐标(x , y)都是这个二元一次方程的解.
思考2:从形的角度看,一次函数与二元一次方程有什么关系?
二元一次方程组的解就是相应的 两个一次函数图象的交点坐标.
思考3:从形的角度看,二元一次方程组与一次函数有什么关系?
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
从数的角度看:
就是求自变量为何值时,两个一次函数 y =x+5,y =0.5x+15 的函数值相等,并求出函数值.
解方程组
y =x+5,
y =0.5x+15
(2)在某时刻两个气球能否位于同一高度?如果能,
这时气球上升了多长时间?位于什么高度?
解方程组
y =x+5,
y =0.5x+15,
∴当上升20 min 时,两个气球都位于海拔25 m的高度.
A(20,25)
30
25
20
15
10
5
y =x+5
y =0.5x+15
O
y
观察图象,两条直线的交点坐标是(20,25).
∴当上升20 min 时,两个气球都位于海拔25 m的高度.
从形的角度看:
一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
方程组的解 对应两条直线交点的坐标.
总结
随堂训练
1、一次函数y=ax+b的图象如图所示,则不等式ax+b≥0的解集是( )
A.x≥2 B.x≤2
C.x≥4 D.x≤4
B
2、小亮用作图象的方法解二元一次方程组时,在
同一直角坐标系内作出了相应的两条直线l1、l2
如图 ,他解的这个方程组是( )
D
点拨:由图象知l1、l2 的 x 的系数都应为负数,排除 A、
C.又 l1、l2的交点为(2,-2),代入验证可知只有 D 符合.
3、如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式-2<kx+b<1的 解集__________ .
-1<x<2
2
1
-2
-1
4、当x 时,直线y=-x+2上的点在x轴的下方.
x
o
y
2
2
5、直线=-x+m和=2x+n的交点如图,则不等式-x+m<2x+n的解集是 .
x
o
y
2
1
>2
x<1
y1=-x+m
y2=2x+n
课堂小结
一次函数与方程、不等式
解一元一次方程 对应一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标
解一元一次不等式 对应一次函数的函数值大(小)于0时,求自变量的取值范围,即在x轴上方(或下方)的图象所对应的x的取值范围
解二元一次方程组 求对应两条直线交点的坐标
