20.1.1 平均数和加权平均数(第2课时)教学课件--人教版初中数学八下
文档属性
| 名称 | 20.1.1 平均数和加权平均数(第2课时)教学课件--人教版初中数学八下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:40 | ||
图片预览




文档简介
(共25张PPT)
第二十章 数据的分析
20.1.1 平均数和加权平均数
第二十章 数据的分析
20.1 数据的集中趋势
第2课时
学 习 目 标
1
3
理解组中值的意义,能利用组中值计算一组数据的加权平均数;(重点)
理解用样本平均数估计总体平均数的意义.(难点)
2
了解使用计算器计算加权平均数.
1.若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,
则__________________叫做这n个数的加权平均数.
旧知回顾
2.“权”反映数据的“重要程度”,其表现形式有:数据所占的百分比、各个数据所占的比值、数据出现的次数.
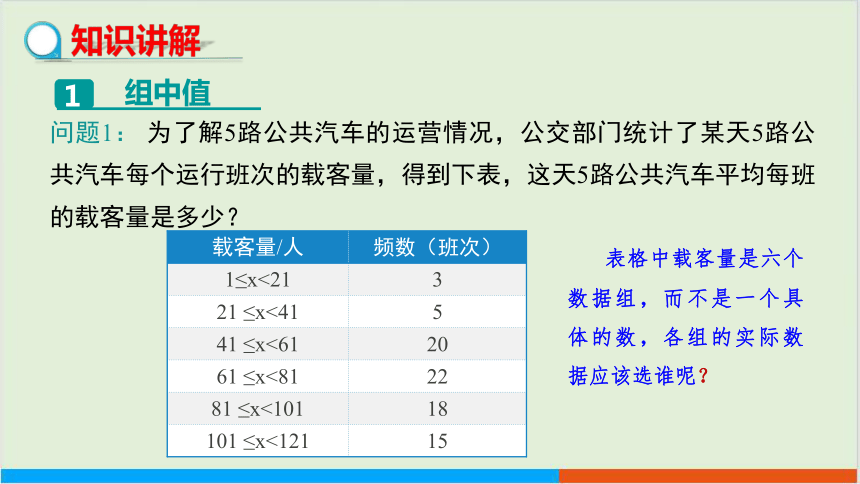
问题1: 为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表,这天5路公共汽车平均每班的载客量是多少?
载客量/人 频数(班次)
1≤x<21 3
21 ≤x<41 5
41 ≤x<61 20
61 ≤x<81 22
81 ≤x<101 18
101 ≤x<121 15
知识讲解
组中值
1
表格中载客量是六个数据组,而不是一个具体的数,各组的实际数据应该选谁呢?
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
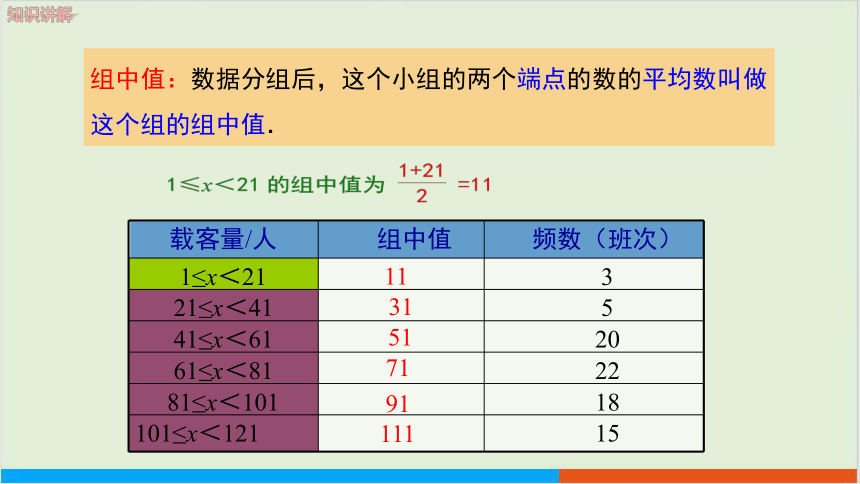
11
31
51
71
91
111
组中值:数据分组后,这个小组的两个端点的数的平均数叫做这个组的组中值.
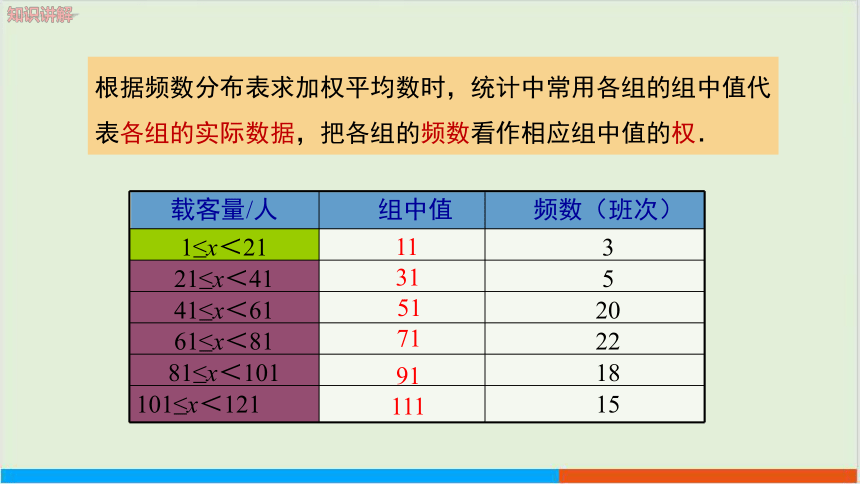
根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权.
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
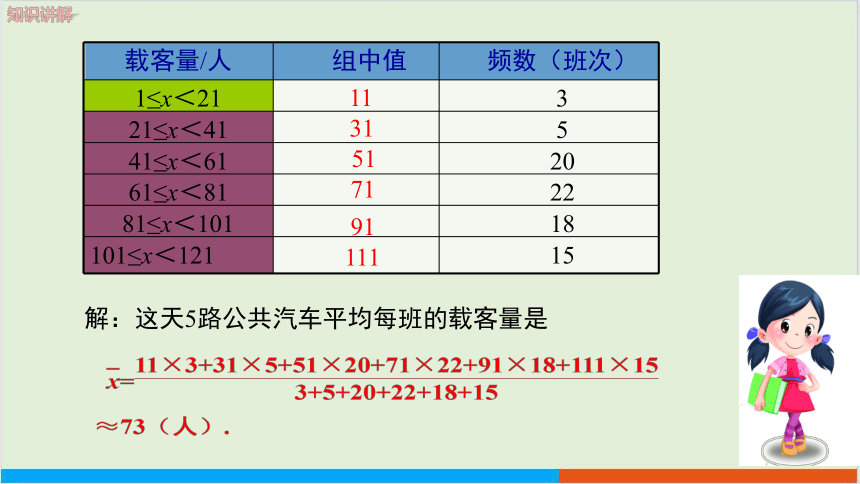
解:这天5路公共汽车平均每班的载客量是
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
1.不同品牌的计算器的操作步骤有所不同,
操作时需要参阅计算器的使用说明书.
2.通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn ,以及它们的权f, f2,…,fn ;
最后按动求平均数的功能键(例如 键),计算器便会求出平均数 的值.
使用计算器计算加权平均数
2
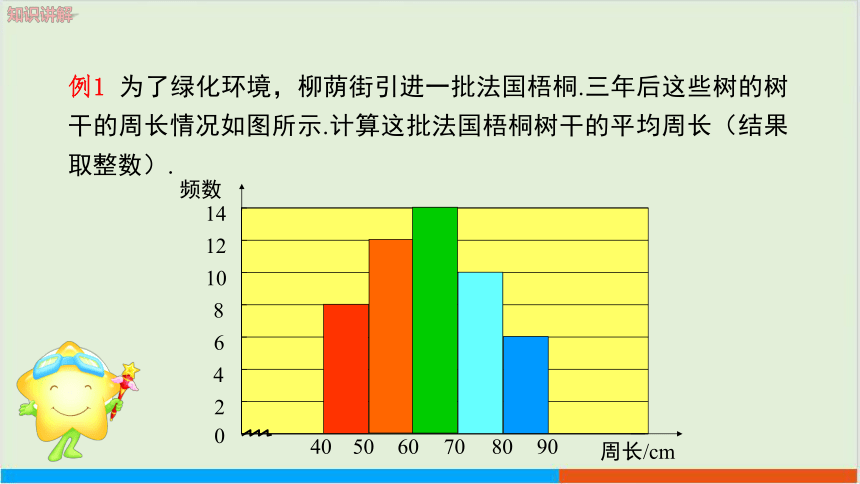
例1 为了绿化环境,柳荫街引进一批法国梧桐.三年后这些树的树干的周长情况如图所示.计算这批法国梧桐树干的平均周长(结果取整数).
0
2
4
6
8
10
12
14
40
50
60
70
80
90
频数
周长/cm
答:这批梧桐树干的平均周长是64cm.
解:
用样本平均数估计总体平均数
3
使用理由
选取样本数据的条件
(1)在很多情况下总体包含的个体数目很多,甚至无限,不可能一一加以考察.
(2)有些从总体中抽取个体的试验带有破坏性,因此抽取个体的数目不允许太多.
选取的样本要有随机性,样本中的数据要有代表性。
否则会影响样本对总体估计的精确度。
问题2 为了了解某校1800名学生的身高情况,随机抽取该校男生和女生进行抽样调查.利用所得数据绘制如下统计图表:
组别 身高/cm
A 145≤x<155
B 155≤x<165
C 165≤x<175
D 175≤x<185
身高情况分组表(单位:cm)
男生身高情况直方图
女生身高情况扇形统计图
组别 身高/cm
A 145≤x<155
B 155≤x<165
C 165≤x<175
D 175≤x<185
身高情况分组表(单位:cm)
男生身高情况直方图
女生身高情况扇形统计图
(1)根据图表提供的信息,样本中男生的平均身高约是多少?
(2)已知抽取的样本中,女生和男生的人数相同,样本中女生的平均身高约是多少?
组别 身高/cm
A 145≤x<155
B 155≤x<165
C 165≤x<175
D 175≤x<185
男生身高情况直方图
女生身高情况扇形统计图
(3)若抽样的女生为m人,女生的平均身高会改变吗?若改变,请计算;若不变,请说明理由.
(4)根据以上结果,你能估计该校女生的平均身高吗?
组别 身高/cm
A 145≤x<155
B 155≤x<165
C 165≤x<175
D 175≤x<185
男生身高情况直方图
女生身高情况扇形统计图
用样本的平均数可以估计总体的平均数.
例2 用商家免费提供的塑料袋购物,我们享受着方便和快捷,但同时要关注它对环境的潜在危害。为了解某市所有家庭每年丢弃塑料袋个数的情况,统计人员采用了科学的方法,随机抽取了200户,对他们某日丢弃塑料袋的个数进行了统计,结果如下表:
(1)求这天这200户家庭平均每户丢弃塑料袋的个数;
(2)假设本市现有家庭100万户,据此估计全市所有家庭每年(以36天计算)丢弃塑料袋的总数.
解:(1)(15×1+60×2+65×3+35×4+20×5+5×6)÷200=3(个),
∴这天这200户家庭平均每户丢弃3个塑料袋.
(2)∵100×3×365=109500(万个),∴全市所有家庭每年约丢弃109500万个塑料袋
年 龄 频数
28≤X<30 4
30≤X<32 4
32≤X<34 8
34≤X<36 8
36≤X<38 12
38≤X<40 14
40≤X<42 6
1.下表是截至到2017年菲尔兹奖得主获奖时的年龄,根据表格中的信息计算获菲尔兹奖得主获奖时的平均年龄(保留一位小数)?
答案:36.1岁.
随堂训练
2.为了检查一批零件的质量,从中随机抽取10件,
测得它们的长度(单位:mm)如下:
22.36 22.35 22.33 22.35 22.37
22.34 22.38 22.36 22.32 22.35
根据以上数据,估计这批零件的平均长度.
解:根据以上数据,得
=
= 22.351
即样本平均数为 22.351
答:这批零件的平均长度大约是22.351mm.
3.下图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.
(1)本次测验的平均分约是多少?
解:(1)∵点D,O,E在同一条直线上,∴∠DOE=180°,
∴60≤x<80所占百分比为180/360 ×100%=50%.
∵∠AOE=36°,
∴80≤x≤100所占百分比为36/360 ×100%=10%,
∴0≤x<20所占百分比为1-50%-25%-10%-10%=5%.
∴本次测验的平均分是
10×5%+30×10%+50×25%+70×50%+90×10%
=60(分)
(2)已知本次测验及格人数比不及格人数(低于60分为不及格)多240人,求参加本次测验的人数.
解:设参加本次测验的有x人,根据题意得
(50%+10%)x-(5%+10%+25%)x=240,
解得x=1200.
即参加本次测验的有1200人.
4.某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
使用寿命 x/h
600≤x
<1 000
1 000≤x
<1 400
1 400≤x
<1 800
1 800≤x
<2 200
2 200≤x
<2 600
灯泡只数
5
10
12
17
6
抽出50只灯泡的使用寿命组成一个样本,可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.
解:据上表得各小组的组中值,于是
即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大约是
1 672 h.
用样本平均数估计总体平均数
组中值是指两个端点的数的平均数;
把各组的频数看作相应组中值的权
用计算器求平均数
用样本平均数估计总体平均数
课堂小结
第二十章 数据的分析
20.1.1 平均数和加权平均数
第二十章 数据的分析
20.1 数据的集中趋势
第2课时
学 习 目 标
1
3
理解组中值的意义,能利用组中值计算一组数据的加权平均数;(重点)
理解用样本平均数估计总体平均数的意义.(难点)
2
了解使用计算器计算加权平均数.
1.若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,
则__________________叫做这n个数的加权平均数.
旧知回顾
2.“权”反映数据的“重要程度”,其表现形式有:数据所占的百分比、各个数据所占的比值、数据出现的次数.
问题1: 为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表,这天5路公共汽车平均每班的载客量是多少?
载客量/人 频数(班次)
1≤x<21 3
21 ≤x<41 5
41 ≤x<61 20
61 ≤x<81 22
81 ≤x<101 18
101 ≤x<121 15
知识讲解
组中值
1
表格中载客量是六个数据组,而不是一个具体的数,各组的实际数据应该选谁呢?
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
组中值:数据分组后,这个小组的两个端点的数的平均数叫做这个组的组中值.
根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权.
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
解:这天5路公共汽车平均每班的载客量是
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
1.不同品牌的计算器的操作步骤有所不同,
操作时需要参阅计算器的使用说明书.
2.通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn ,以及它们的权f, f2,…,fn ;
最后按动求平均数的功能键(例如 键),计算器便会求出平均数 的值.
使用计算器计算加权平均数
2
例1 为了绿化环境,柳荫街引进一批法国梧桐.三年后这些树的树干的周长情况如图所示.计算这批法国梧桐树干的平均周长(结果取整数).
0
2
4
6
8
10
12
14
40
50
60
70
80
90
频数
周长/cm
答:这批梧桐树干的平均周长是64cm.
解:
用样本平均数估计总体平均数
3
使用理由
选取样本数据的条件
(1)在很多情况下总体包含的个体数目很多,甚至无限,不可能一一加以考察.
(2)有些从总体中抽取个体的试验带有破坏性,因此抽取个体的数目不允许太多.
选取的样本要有随机性,样本中的数据要有代表性。
否则会影响样本对总体估计的精确度。
问题2 为了了解某校1800名学生的身高情况,随机抽取该校男生和女生进行抽样调查.利用所得数据绘制如下统计图表:
组别 身高/cm
A 145≤x<155
B 155≤x<165
C 165≤x<175
D 175≤x<185
身高情况分组表(单位:cm)
男生身高情况直方图
女生身高情况扇形统计图
组别 身高/cm
A 145≤x<155
B 155≤x<165
C 165≤x<175
D 175≤x<185
身高情况分组表(单位:cm)
男生身高情况直方图
女生身高情况扇形统计图
(1)根据图表提供的信息,样本中男生的平均身高约是多少?
(2)已知抽取的样本中,女生和男生的人数相同,样本中女生的平均身高约是多少?
组别 身高/cm
A 145≤x<155
B 155≤x<165
C 165≤x<175
D 175≤x<185
男生身高情况直方图
女生身高情况扇形统计图
(3)若抽样的女生为m人,女生的平均身高会改变吗?若改变,请计算;若不变,请说明理由.
(4)根据以上结果,你能估计该校女生的平均身高吗?
组别 身高/cm
A 145≤x<155
B 155≤x<165
C 165≤x<175
D 175≤x<185
男生身高情况直方图
女生身高情况扇形统计图
用样本的平均数可以估计总体的平均数.
例2 用商家免费提供的塑料袋购物,我们享受着方便和快捷,但同时要关注它对环境的潜在危害。为了解某市所有家庭每年丢弃塑料袋个数的情况,统计人员采用了科学的方法,随机抽取了200户,对他们某日丢弃塑料袋的个数进行了统计,结果如下表:
(1)求这天这200户家庭平均每户丢弃塑料袋的个数;
(2)假设本市现有家庭100万户,据此估计全市所有家庭每年(以36天计算)丢弃塑料袋的总数.
解:(1)(15×1+60×2+65×3+35×4+20×5+5×6)÷200=3(个),
∴这天这200户家庭平均每户丢弃3个塑料袋.
(2)∵100×3×365=109500(万个),∴全市所有家庭每年约丢弃109500万个塑料袋
年 龄 频数
28≤X<30 4
30≤X<32 4
32≤X<34 8
34≤X<36 8
36≤X<38 12
38≤X<40 14
40≤X<42 6
1.下表是截至到2017年菲尔兹奖得主获奖时的年龄,根据表格中的信息计算获菲尔兹奖得主获奖时的平均年龄(保留一位小数)?
答案:36.1岁.
随堂训练
2.为了检查一批零件的质量,从中随机抽取10件,
测得它们的长度(单位:mm)如下:
22.36 22.35 22.33 22.35 22.37
22.34 22.38 22.36 22.32 22.35
根据以上数据,估计这批零件的平均长度.
解:根据以上数据,得
=
= 22.351
即样本平均数为 22.351
答:这批零件的平均长度大约是22.351mm.
3.下图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.
(1)本次测验的平均分约是多少?
解:(1)∵点D,O,E在同一条直线上,∴∠DOE=180°,
∴60≤x<80所占百分比为180/360 ×100%=50%.
∵∠AOE=36°,
∴80≤x≤100所占百分比为36/360 ×100%=10%,
∴0≤x<20所占百分比为1-50%-25%-10%-10%=5%.
∴本次测验的平均分是
10×5%+30×10%+50×25%+70×50%+90×10%
=60(分)
(2)已知本次测验及格人数比不及格人数(低于60分为不及格)多240人,求参加本次测验的人数.
解:设参加本次测验的有x人,根据题意得
(50%+10%)x-(5%+10%+25%)x=240,
解得x=1200.
即参加本次测验的有1200人.
4.某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
使用寿命 x/h
600≤x
<1 000
1 000≤x
<1 400
1 400≤x
<1 800
1 800≤x
<2 200
2 200≤x
<2 600
灯泡只数
5
10
12
17
6
抽出50只灯泡的使用寿命组成一个样本,可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.
解:据上表得各小组的组中值,于是
即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大约是
1 672 h.
用样本平均数估计总体平均数
组中值是指两个端点的数的平均数;
把各组的频数看作相应组中值的权
用计算器求平均数
用样本平均数估计总体平均数
课堂小结
