9.1.1认识三角形(第1课时三角形的有关概念) 教学课件--华师大版初中数学七年级(下)
文档属性
| 名称 | 9.1.1认识三角形(第1课时三角形的有关概念) 教学课件--华师大版初中数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第 9章 多边形
9.1 三角形
第1课时 三角形的有关概念
9.1.1 认识三角形
学 习 目 标
1.认识三角形并会用几何语言表示三角形;
2.掌握三角形分类.
新课导入
思考
探究
(1)从古埃及的金字塔到现代的飞机,从宏伟的建筑到微小的分子结构,都有什么样的形象?
(2)在我们的生活中有没有这样的形象呢?试举例.
从古埃及的金字塔到现代的飞机,从宏大的建筑到微小的分子结构, 处处都有三角形的身影.
交通标志、警告牌、三明治等等.
知识讲解
三角形的有关概念
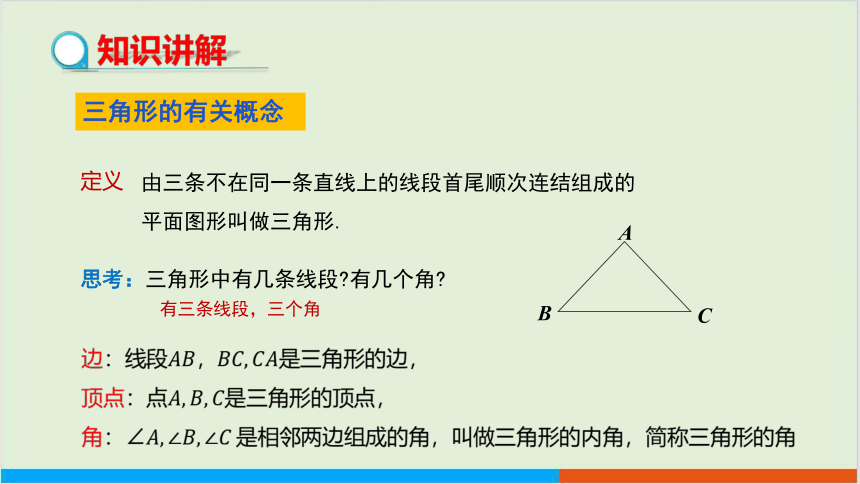
由三条不在同一条直线上的线段首尾顺次连结组成的平面图形叫做三角形.
定义
思考:三角形中有几条线段 有几个角
有三条线段,三个角
A
B
C
边:线段是三角形的边,
顶点:点是三角形的顶点,
角:∠是相邻两边组成的角,叫做三角形的内角,简称三角形的角
的三边 , 来表示.
三角形的表示
三角形可以用符号“△”表示,顶点是的三角形,记作,读作“三角形”.
边的表示
∠所对的边是, ∠所对的边是, ∠所对的边是.
角的对边
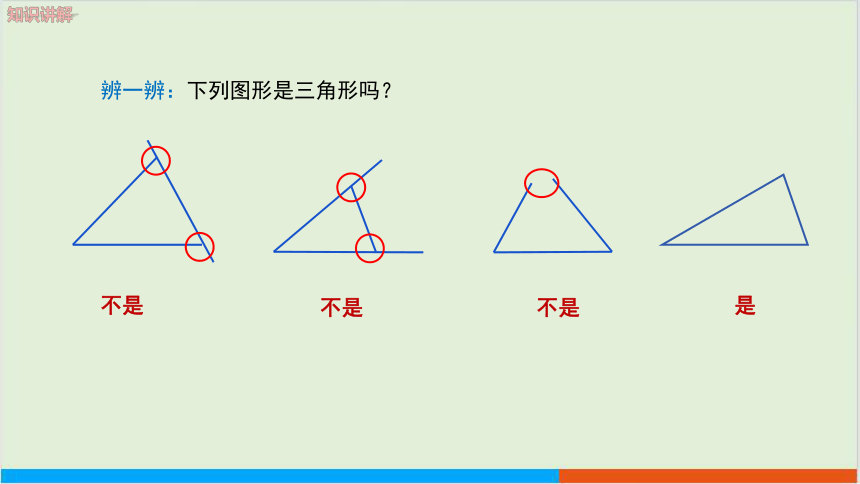
辨一辨:下列图形是三角形吗?
不是
不是
是
不是
①位置关系:不在同一直线上;
②联接方式:首尾顺次相接.
三角形应满足以下两个条件:
要点提醒
表示方法:
三角形用符号“△”表示;记作“△ABC”,读作“三角形ABC”,除此△ABC还可记作△BCA, △ CAB, △ ACB等.
思考:如图,把△ABC的一边BC延长,得到∠ACD.它与 △ABC有和联系呢?
像这样,三角形的一边与另一边的延长线所组成的角,叫作三角形的外角.
对外角∠ACD来说,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角.
D
三角形的分类
锐角三角形
钝角三角形
直角三角形
思考:按照三角形内角的大小,三角形可以分为哪几类?
直角三角形
锐角三角形
钝角三角形
三角形
三角形按角的大小分类
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
问题:你能找出下列三角形各自的特点吗?
三边均不相等
有两条边相等
三条边均相等
三条边各不相等的三角形叫作不等边三角形 ;
有两条边相等的三角形叫作等腰三角形;
三条边都相等的三角形叫作等边三角形.
等边三角形和等腰三角形之间有什么关系?
总结归纳
等腰三角形两边相等,等边三角形三边相等.
我们可以把三角形按照三边情况进行分类
三角形按边的相等关系分类
三角形
不等边三角形
等腰三角形
腰和底不等的三角形
等边三角形
随堂训练
(2)等边三角形是特殊的等腰三角形.( )
(1)一个钝角三角形一定不是等腰三角形.( )
(3)等腰三角形的腰和底一定不相等.( )
(5)直角三角形一定不是等腰三角形.( )
1.判断:
√
×
×
(4)等边三角形是锐角三角形.( )
×
√
2.图中锐角三角形的个数有( )
A.3个 B.4个 C.5个 D.6个
A
3.如果等腰三角形的一边长是5cm,另一边长是8cm, 则这个等腰三角形的周长为______________.
18cm或21cm
课堂小结
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类
第 9章 多边形
9.1 三角形
第1课时 三角形的有关概念
9.1.1 认识三角形
学 习 目 标
1.认识三角形并会用几何语言表示三角形;
2.掌握三角形分类.
新课导入
思考
探究
(1)从古埃及的金字塔到现代的飞机,从宏伟的建筑到微小的分子结构,都有什么样的形象?
(2)在我们的生活中有没有这样的形象呢?试举例.
从古埃及的金字塔到现代的飞机,从宏大的建筑到微小的分子结构, 处处都有三角形的身影.
交通标志、警告牌、三明治等等.
知识讲解
三角形的有关概念
由三条不在同一条直线上的线段首尾顺次连结组成的平面图形叫做三角形.
定义
思考:三角形中有几条线段 有几个角
有三条线段,三个角
A
B
C
边:线段是三角形的边,
顶点:点是三角形的顶点,
角:∠是相邻两边组成的角,叫做三角形的内角,简称三角形的角
的三边 , 来表示.
三角形的表示
三角形可以用符号“△”表示,顶点是的三角形,记作,读作“三角形”.
边的表示
∠所对的边是, ∠所对的边是, ∠所对的边是.
角的对边
辨一辨:下列图形是三角形吗?
不是
不是
是
不是
①位置关系:不在同一直线上;
②联接方式:首尾顺次相接.
三角形应满足以下两个条件:
要点提醒
表示方法:
三角形用符号“△”表示;记作“△ABC”,读作“三角形ABC”,除此△ABC还可记作△BCA, △ CAB, △ ACB等.
思考:如图,把△ABC的一边BC延长,得到∠ACD.它与 △ABC有和联系呢?
像这样,三角形的一边与另一边的延长线所组成的角,叫作三角形的外角.
对外角∠ACD来说,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角.
D
三角形的分类
锐角三角形
钝角三角形
直角三角形
思考:按照三角形内角的大小,三角形可以分为哪几类?
直角三角形
锐角三角形
钝角三角形
三角形
三角形按角的大小分类
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
问题:你能找出下列三角形各自的特点吗?
三边均不相等
有两条边相等
三条边均相等
三条边各不相等的三角形叫作不等边三角形 ;
有两条边相等的三角形叫作等腰三角形;
三条边都相等的三角形叫作等边三角形.
等边三角形和等腰三角形之间有什么关系?
总结归纳
等腰三角形两边相等,等边三角形三边相等.
我们可以把三角形按照三边情况进行分类
三角形按边的相等关系分类
三角形
不等边三角形
等腰三角形
腰和底不等的三角形
等边三角形
随堂训练
(2)等边三角形是特殊的等腰三角形.( )
(1)一个钝角三角形一定不是等腰三角形.( )
(3)等腰三角形的腰和底一定不相等.( )
(5)直角三角形一定不是等腰三角形.( )
1.判断:
√
×
×
(4)等边三角形是锐角三角形.( )
×
√
2.图中锐角三角形的个数有( )
A.3个 B.4个 C.5个 D.6个
A
3.如果等腰三角形的一边长是5cm,另一边长是8cm, 则这个等腰三角形的周长为______________.
18cm或21cm
课堂小结
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类
