9.1.1认识三角形(第2课时三角形中的重要线段) 教学课件--华师大版初中数学七年级(下)
文档属性
| 名称 | 9.1.1认识三角形(第2课时三角形中的重要线段) 教学课件--华师大版初中数学七年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:32:27 | ||
图片预览






文档简介
(共19张PPT)
第 9章 多边形
9.1 三角形
第2课时 三角形中的重要线段
9.1.1 认识三角形
学 习 目 标
1.掌握三角形的高,中线及角平分线的概念.(重点)
2.掌握三角形的高,中线及角平分线的画法.
3.掌握钝角三角形的两短边上高的画法.(难点)
新课导入
1.过直线外一点,画已知直线的垂线,能画几条,
怎么画?
只能画一条.
2.已知△ABC中,BC=5cm,高AD=4cm,求△ABC的
面积.
★ 三角形的中线
连接三角形的一个顶点和它所对的中点的线段叫做三角形的中线.如图,是△的边上的中线.
定义
中线
中点
想一想:由三角形的中线能得到什么结论?
(或为的中点)
知识讲解
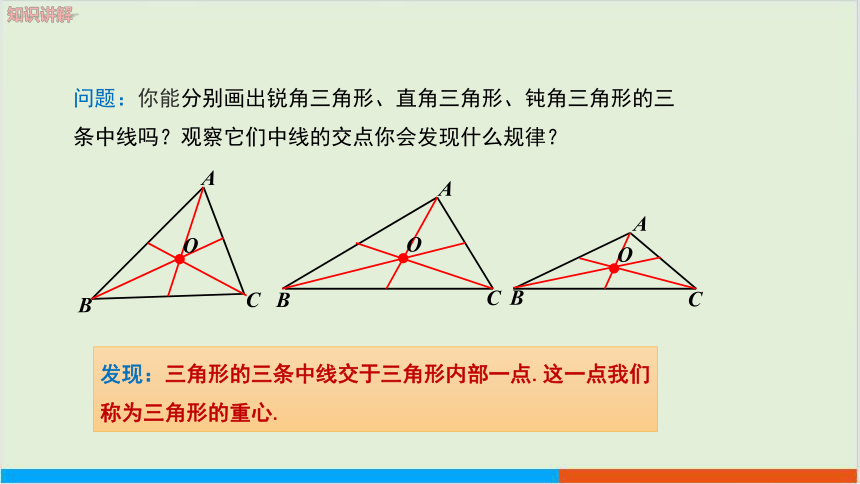
问题:你能分别画出锐角三角形、直角三角形、钝角三角形的三条中线吗?观察它们中线的交点你会发现什么规律?
发现:三角形的三条中线交于三角形内部一点.这一点我们称为三角形的重心.
A
B
C
A
B
C
A
B
C
O
O
O
拓展: 如图所示,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?你能发现什么规律?
B
C
D
E
A
相等,因为两个三角形等底同高,所以它们面积相等.
发现:三角形的中线能将三角形的面积平分.
★ 三角形的角平分线
在三角形中,一个内角的平分线和它所对的边相交于一点,这个角的顶点与交点之间的线段叫做三角形的角平分线.如图, 是△ 的角平分线, 或∠ =∠ = ∠且点在边 上.
1
2
A
C
D
∠1=∠2
B
想一想:三角形的角平分线与角的角平分线相同吗
定义
不同,三角形的角平分线是线段,而角的平分线是射线
问题:请画出这个三角形的另外两条角平分线,你发现了什么?
A
B
C
D
E
F
发现:三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心.
问题:分别画出锐角三角形、直角三角形、钝角三角形的三条角平分线,观察它们是否也有这样的发现?
★ 三角形的高
定义
A
B
C
从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
D
注意:标明垂直的记号和垂足的字母.
如图,从△ABC的顶点A向它的对边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
垂足
问题:(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
(3) 锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高交于同一点;
锐角三角形的三条高都在三角形的内部.
如图所示;
锐角三角形的三条高
F
E
A
B
O
C
D
直角三角形的三条高
问题: 画出直角三角形的三条高,直角三角形的三条高又有怎样的位置关系吗
A
B
C
D
直角三角形的三条高交于直角顶点.
直角边BC边上的高是 ;
直角边AB边上的高是 ;
AC边上的高是 ;
AB
BC
BD
钝角三角形的三条高
问题: 画出钝角三角形的三条高,钝角三角形的三条高又有怎样的位置关系吗
A
B
D
F
O
E
C
钝角三角形的三条高不相交于一点,钝角三角形的三条高所在直线交于一点
要点归纳
随堂训练
1.下列四个图形中,线段BE是△ABC的高的图形是( )
A
2.如图,用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是( )
B
3.下列说法错误的是( )
A.三角形的高、中线、角平分线都是线段
B.三角形的三条中线都在三角形内部
C.锐角三角形的三条高一定交于同一点
D.三角形的三条高、三条中线、三条角平分线都交于同一点
D
4.如图所示,BD是△ABC的中线,AD=2,AB+BC=5,求△ABC的周长.
解:因为BD是△ABC的中线,
所以点D是AC的中点,
所以AC=2AD=4,
所以△ABC的周长为AB+BC+AC=5+4=9.
课堂小结
三角形重要线段
高
锐角三角形的三条高交于在三角形的内部一点,直角三角形的三条高交于直角顶点,钝角三角形的三条高所在直线交于三角形外部一点
中线
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心
一边上的中线把原三角形分成两个面积相等的三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心
第 9章 多边形
9.1 三角形
第2课时 三角形中的重要线段
9.1.1 认识三角形
学 习 目 标
1.掌握三角形的高,中线及角平分线的概念.(重点)
2.掌握三角形的高,中线及角平分线的画法.
3.掌握钝角三角形的两短边上高的画法.(难点)
新课导入
1.过直线外一点,画已知直线的垂线,能画几条,
怎么画?
只能画一条.
2.已知△ABC中,BC=5cm,高AD=4cm,求△ABC的
面积.
★ 三角形的中线
连接三角形的一个顶点和它所对的中点的线段叫做三角形的中线.如图,是△的边上的中线.
定义
中线
中点
想一想:由三角形的中线能得到什么结论?
(或为的中点)
知识讲解
问题:你能分别画出锐角三角形、直角三角形、钝角三角形的三条中线吗?观察它们中线的交点你会发现什么规律?
发现:三角形的三条中线交于三角形内部一点.这一点我们称为三角形的重心.
A
B
C
A
B
C
A
B
C
O
O
O
拓展: 如图所示,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?你能发现什么规律?
B
C
D
E
A
相等,因为两个三角形等底同高,所以它们面积相等.
发现:三角形的中线能将三角形的面积平分.
★ 三角形的角平分线
在三角形中,一个内角的平分线和它所对的边相交于一点,这个角的顶点与交点之间的线段叫做三角形的角平分线.如图, 是△ 的角平分线, 或∠ =∠ = ∠且点在边 上.
1
2
A
C
D
∠1=∠2
B
想一想:三角形的角平分线与角的角平分线相同吗
定义
不同,三角形的角平分线是线段,而角的平分线是射线
问题:请画出这个三角形的另外两条角平分线,你发现了什么?
A
B
C
D
E
F
发现:三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心.
问题:分别画出锐角三角形、直角三角形、钝角三角形的三条角平分线,观察它们是否也有这样的发现?
★ 三角形的高
定义
A
B
C
从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
D
注意:标明垂直的记号和垂足的字母.
如图,从△ABC的顶点A向它的对边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
垂足
问题:(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
(3) 锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高交于同一点;
锐角三角形的三条高都在三角形的内部.
如图所示;
锐角三角形的三条高
F
E
A
B
O
C
D
直角三角形的三条高
问题: 画出直角三角形的三条高,直角三角形的三条高又有怎样的位置关系吗
A
B
C
D
直角三角形的三条高交于直角顶点.
直角边BC边上的高是 ;
直角边AB边上的高是 ;
AC边上的高是 ;
AB
BC
BD
钝角三角形的三条高
问题: 画出钝角三角形的三条高,钝角三角形的三条高又有怎样的位置关系吗
A
B
D
F
O
E
C
钝角三角形的三条高不相交于一点,钝角三角形的三条高所在直线交于一点
要点归纳
随堂训练
1.下列四个图形中,线段BE是△ABC的高的图形是( )
A
2.如图,用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是( )
B
3.下列说法错误的是( )
A.三角形的高、中线、角平分线都是线段
B.三角形的三条中线都在三角形内部
C.锐角三角形的三条高一定交于同一点
D.三角形的三条高、三条中线、三条角平分线都交于同一点
D
4.如图所示,BD是△ABC的中线,AD=2,AB+BC=5,求△ABC的周长.
解:因为BD是△ABC的中线,
所以点D是AC的中点,
所以AC=2AD=4,
所以△ABC的周长为AB+BC+AC=5+4=9.
课堂小结
三角形重要线段
高
锐角三角形的三条高交于在三角形的内部一点,直角三角形的三条高交于直角顶点,钝角三角形的三条高所在直线交于三角形外部一点
中线
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心
一边上的中线把原三角形分成两个面积相等的三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心
