9.1.3三角形的三边关系 教学课件--华师大版初中数学七年级(下)
文档属性
| 名称 | 9.1.3三角形的三边关系 教学课件--华师大版初中数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:32:27 | ||
图片预览





文档简介
(共18张PPT)
第 9章 多边形
9.1 三角形
9.1.3 三角形的三边关系
学 习 目 标
1.掌握“三角形的任意两边之和大于第三边”的性
质并能初步运用;(重点、难点)
2.了解三角形的稳定性及应用.
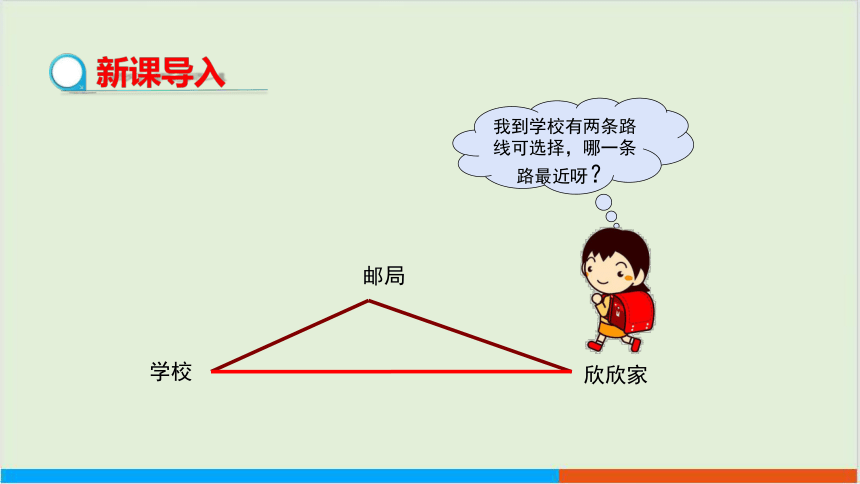
新课导入
我到学校有两条路线可选择,哪一条路最近呀?
邮局
学校
欣欣家
知识讲解
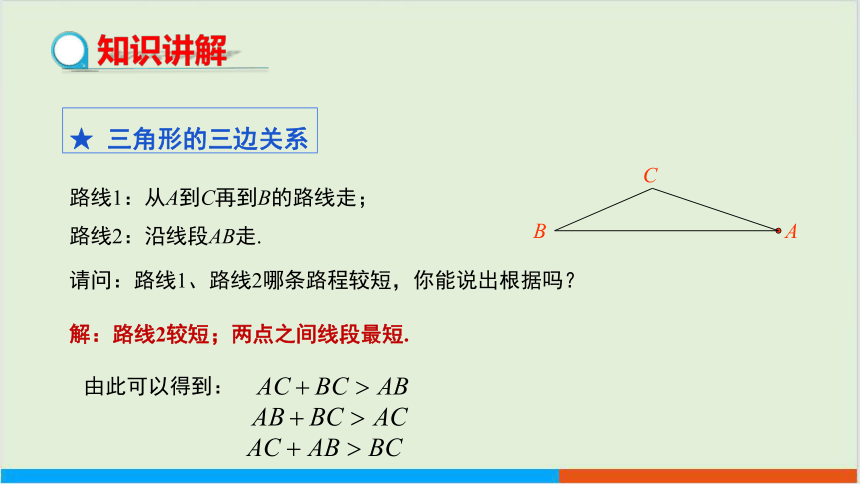
★ 三角形的三边关系
路线1:从A到C再到B的路线走;
路线2:沿线段AB走.
请问:路线1、路线2哪条路程较短,你能说出根据吗?
解:路线2较短;两点之间线段最短.
由此可以得到:
A
B
C
三角形任意两边的和大于第三边
想一想:由不等式的变形,三角形的两边之差与第
三边有何关系?
三角形任意两边的差小于第三边
三角形三边的关系定理的理论根据是?
三角形的三边关系定理
两点之间,线段最短.
例1 判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;
(3)5cm、6cm、10cm.
归纳:判断三条线段是否可以组成三角形,只需说明两条较短线段之和大于第三条线段即可.
解:(1)不能,因为3cm+4cm<8cm;
(2)不能,因为5cm+6cm=11cm;
(3)能,因为5cm+6cm>10cm.
解析:∵三角形的三边长分别为4,7,x,
∴7-4<x<7+4,即3<x<11.
例2 一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
总结:判断三角形边的取值范围要同时运用两边之和大于第三边,两边之差小于第三边.
★ 三角形的稳定性
探究1:如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
不会改变,也就是说,三角形的三条边长确定后,三角形的形状就确定了.
探究2:如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
会改变,也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变.
探究3:如图,四边形木架上再钉一根木条,将它的一对不相等的顶点连接起来,然后再扭动它,这时木架的形状会改变吗?为什么?
不会改变,三角形具有稳定性,四边形不具有稳定性.
理解“稳定性”
“只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
这就是说,三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形边长确定,其形状和大小就确定了”.
例3 小明用7 根木条钉成一个七边形的木架,他为了使该木架稳固, 想在其中加上四根木条,请你在下图的三个图中画出你的三种想法.
解:如图所示(答案不唯一).
1.下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
随堂训练
4.如果等腰三角形的一边长是4cm,另一边长是9cm,
则这个等腰三角形的周长为______________.
3.如果等腰三角形的一边长是5cm,另一边长是8cm,
则这个等腰三角形的周长为______________.
2.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中
三条线段为边长可以构成________个三角形.
3
22cm
18cm或21cm
5.小颖要制作一个三角形木架,现有两根长度为8cm
和5cm的木棒,如果要求第三根木棒的长度是偶数,
小颖有几种选法?第三根的长度可以是多少?
∵x为偶数,∴小颖有5种选法
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm.
解:设第三根木棒长为xcm,有
8-5<x<8+5
3<x<13
6.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
三角形的三边关系
三角形的三边关系:任何两边的和大于第三边,任何两边的差小于第三边.
应用
稳定性
三角形
独有性质
应用
课堂小结
第 9章 多边形
9.1 三角形
9.1.3 三角形的三边关系
学 习 目 标
1.掌握“三角形的任意两边之和大于第三边”的性
质并能初步运用;(重点、难点)
2.了解三角形的稳定性及应用.
新课导入
我到学校有两条路线可选择,哪一条路最近呀?
邮局
学校
欣欣家
知识讲解
★ 三角形的三边关系
路线1:从A到C再到B的路线走;
路线2:沿线段AB走.
请问:路线1、路线2哪条路程较短,你能说出根据吗?
解:路线2较短;两点之间线段最短.
由此可以得到:
A
B
C
三角形任意两边的和大于第三边
想一想:由不等式的变形,三角形的两边之差与第
三边有何关系?
三角形任意两边的差小于第三边
三角形三边的关系定理的理论根据是?
三角形的三边关系定理
两点之间,线段最短.
例1 判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;
(3)5cm、6cm、10cm.
归纳:判断三条线段是否可以组成三角形,只需说明两条较短线段之和大于第三条线段即可.
解:(1)不能,因为3cm+4cm<8cm;
(2)不能,因为5cm+6cm=11cm;
(3)能,因为5cm+6cm>10cm.
解析:∵三角形的三边长分别为4,7,x,
∴7-4<x<7+4,即3<x<11.
例2 一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
总结:判断三角形边的取值范围要同时运用两边之和大于第三边,两边之差小于第三边.
★ 三角形的稳定性
探究1:如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
不会改变,也就是说,三角形的三条边长确定后,三角形的形状就确定了.
探究2:如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
会改变,也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变.
探究3:如图,四边形木架上再钉一根木条,将它的一对不相等的顶点连接起来,然后再扭动它,这时木架的形状会改变吗?为什么?
不会改变,三角形具有稳定性,四边形不具有稳定性.
理解“稳定性”
“只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
这就是说,三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形边长确定,其形状和大小就确定了”.
例3 小明用7 根木条钉成一个七边形的木架,他为了使该木架稳固, 想在其中加上四根木条,请你在下图的三个图中画出你的三种想法.
解:如图所示(答案不唯一).
1.下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
随堂训练
4.如果等腰三角形的一边长是4cm,另一边长是9cm,
则这个等腰三角形的周长为______________.
3.如果等腰三角形的一边长是5cm,另一边长是8cm,
则这个等腰三角形的周长为______________.
2.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中
三条线段为边长可以构成________个三角形.
3
22cm
18cm或21cm
5.小颖要制作一个三角形木架,现有两根长度为8cm
和5cm的木棒,如果要求第三根木棒的长度是偶数,
小颖有几种选法?第三根的长度可以是多少?
∵x为偶数,∴小颖有5种选法
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm.
解:设第三根木棒长为xcm,有
8-5<x<8+5
3<x<13
6.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
三角形的三边关系
三角形的三边关系:任何两边的和大于第三边,任何两边的差小于第三边.
应用
稳定性
三角形
独有性质
应用
课堂小结
