10.1.2轴对称的再认识 教学课件--华师大版初中数学七年级(下)
文档属性
| 名称 | 10.1.2轴对称的再认识 教学课件--华师大版初中数学七年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:32:27 | ||
图片预览





文档简介
(共18张PPT)
第 10章 多边形
10.1 轴对称
10.1.2 轴对称的再认识
学 习 目 标
1.探索轴对称现象共同特点.(重点)
2.轴对称图形与垂直平分线的联系.(重点)
3.垂直平分线的性质与运用.(难点)
新课导入
什么是轴对称图形?什么是图形成轴对称?它们有什么共同的特征?
知识讲解
垂直平分线
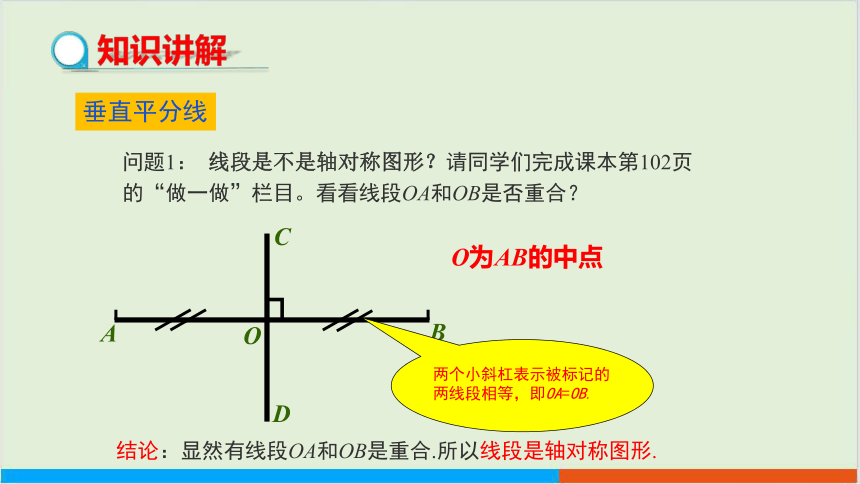
问题1: 线段是不是轴对称图形?请同学们完成课本第102页的“做一做”栏目。看看线段OA和OB是否重合?
结论:显然有线段OA和OB是重合.所以线段是轴对称图形.
A
B
O
C
D
O为AB的中点
两个小斜杠表示被标记的
两线段相等,即OA=OB.
根据刚才的实验,我们知道线段AB是轴对称图形。直线CD是它的对称轴。直线CD既垂直于线段AB,又平分线AB。
定义:垂直并且平分一条线段的直线称为这条线段垂直平分线,又叫中垂线.
概 括
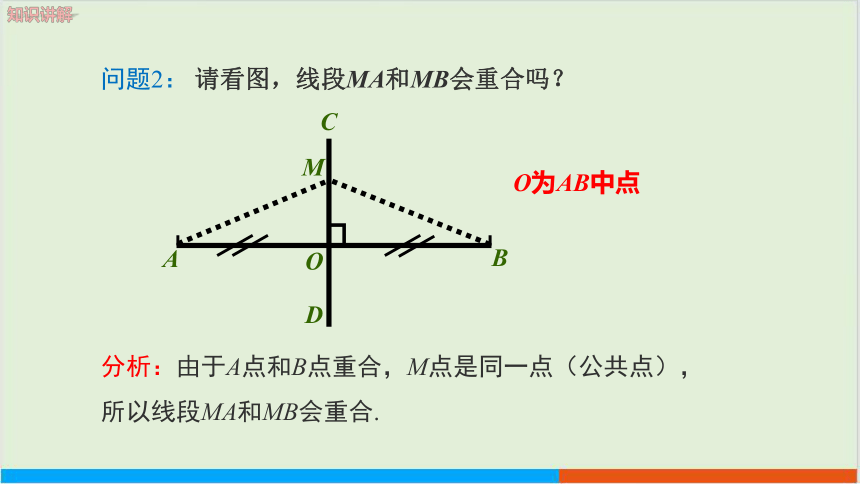
问题2: 请看图,线段MA和MB会重合吗?
A
B
O
C
D
O为AB中点
M
分析:由于A点和B点重合,M点是同一点(公共点),所以线段MA和MB会重合.
线段垂直平分线的性质:线段的垂直平分线上的点到这条线段两个端点的距离相等。
例1 △ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D;BE=6,求△BCE的周长.
解:∵ED是BC的垂直平分线(已知),
∴EC=EB=6(线段的垂直平分线上的点到这条线段两个端点的距离 相等),
∴△BCE的周长=BC+CE+EB=10+6+6=22,
答:△BCE的周长为22.
问题2: 角是不是轴对称图形?
试验:在半透明的纸上画∠AOB,对折,使角的两条边完全重合,然后用直尺画出折痕OM.
从上面试验可以看出,角是轴对称图形,对称轴是它的角平分线所在的直线.
A
B
O
P
结论:角是轴对称图形,对称轴是它的角平分线
所在的直线.
轴对称图形的对称轴的画法
试一试:画出下列图形的对称轴.
如果没有方格子,而又不能折叠,你还能比较准确的画出图形的对称轴吗?
做一做
1.画出下面图形的对称轴,画完图后请思考下面的
问题:
①能总结你画对称轴的方法吗?
②连结对称点的线段与对称轴有什么关系?
连结对称点的线段被对称轴垂直平分
2.如图,点A和点A’关于某条直线成轴对称,你能画
出这条直线吗?
A . . A’
画图形的对称轴的画法:
(2)连结对称点.
(3)画出对称点所连线段的垂直平分线,
就可以得到该图形的对称轴.
结论:如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
(1)找出图形的任意一组对称点.
随堂训练
1.找出下面每个轴对称图形的对称轴.
2.判断题(对的在题后的括号内打“√”,错的打
“×”)
(1) 线段的垂直平分线上存在到这条线段两端点
距离不相等的点 . ( )
(2) 有一公共端点的两条相等线段组成的图形是
轴对称图形 . ( )
(3) 角是轴对称图形,对称轴是角平分线.
( )
×
√
×
A
B
C
3. 如图,A、B、C三点表示三个镇的地理位置,随着乡
镇外资、集体、个体工业的发展需要,现三镇联合建
造一个变电所,要求变电所到三镇的距离相等,请你
作出变电所的位置(用点P表示)
作法:
1.分别连结AB、BC.
2.分别作线段AB、BC的垂直平分
线两直线交于点P.
则点P为所求的变电所的位置.
P
课堂小结
线段垂直平分线的定义
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
如果两个图形关于某条直线对称,那么任何一对对称点所连线段的垂直平分线就是该图形的对称轴.
轴对称图形与垂直平分线的联系
第 10章 多边形
10.1 轴对称
10.1.2 轴对称的再认识
学 习 目 标
1.探索轴对称现象共同特点.(重点)
2.轴对称图形与垂直平分线的联系.(重点)
3.垂直平分线的性质与运用.(难点)
新课导入
什么是轴对称图形?什么是图形成轴对称?它们有什么共同的特征?
知识讲解
垂直平分线
问题1: 线段是不是轴对称图形?请同学们完成课本第102页的“做一做”栏目。看看线段OA和OB是否重合?
结论:显然有线段OA和OB是重合.所以线段是轴对称图形.
A
B
O
C
D
O为AB的中点
两个小斜杠表示被标记的
两线段相等,即OA=OB.
根据刚才的实验,我们知道线段AB是轴对称图形。直线CD是它的对称轴。直线CD既垂直于线段AB,又平分线AB。
定义:垂直并且平分一条线段的直线称为这条线段垂直平分线,又叫中垂线.
概 括
问题2: 请看图,线段MA和MB会重合吗?
A
B
O
C
D
O为AB中点
M
分析:由于A点和B点重合,M点是同一点(公共点),所以线段MA和MB会重合.
线段垂直平分线的性质:线段的垂直平分线上的点到这条线段两个端点的距离相等。
例1 △ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D;BE=6,求△BCE的周长.
解:∵ED是BC的垂直平分线(已知),
∴EC=EB=6(线段的垂直平分线上的点到这条线段两个端点的距离 相等),
∴△BCE的周长=BC+CE+EB=10+6+6=22,
答:△BCE的周长为22.
问题2: 角是不是轴对称图形?
试验:在半透明的纸上画∠AOB,对折,使角的两条边完全重合,然后用直尺画出折痕OM.
从上面试验可以看出,角是轴对称图形,对称轴是它的角平分线所在的直线.
A
B
O
P
结论:角是轴对称图形,对称轴是它的角平分线
所在的直线.
轴对称图形的对称轴的画法
试一试:画出下列图形的对称轴.
如果没有方格子,而又不能折叠,你还能比较准确的画出图形的对称轴吗?
做一做
1.画出下面图形的对称轴,画完图后请思考下面的
问题:
①能总结你画对称轴的方法吗?
②连结对称点的线段与对称轴有什么关系?
连结对称点的线段被对称轴垂直平分
2.如图,点A和点A’关于某条直线成轴对称,你能画
出这条直线吗?
A . . A’
画图形的对称轴的画法:
(2)连结对称点.
(3)画出对称点所连线段的垂直平分线,
就可以得到该图形的对称轴.
结论:如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
(1)找出图形的任意一组对称点.
随堂训练
1.找出下面每个轴对称图形的对称轴.
2.判断题(对的在题后的括号内打“√”,错的打
“×”)
(1) 线段的垂直平分线上存在到这条线段两端点
距离不相等的点 . ( )
(2) 有一公共端点的两条相等线段组成的图形是
轴对称图形 . ( )
(3) 角是轴对称图形,对称轴是角平分线.
( )
×
√
×
A
B
C
3. 如图,A、B、C三点表示三个镇的地理位置,随着乡
镇外资、集体、个体工业的发展需要,现三镇联合建
造一个变电所,要求变电所到三镇的距离相等,请你
作出变电所的位置(用点P表示)
作法:
1.分别连结AB、BC.
2.分别作线段AB、BC的垂直平分
线两直线交于点P.
则点P为所求的变电所的位置.
P
课堂小结
线段垂直平分线的定义
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
如果两个图形关于某条直线对称,那么任何一对对称点所连线段的垂直平分线就是该图形的对称轴.
轴对称图形与垂直平分线的联系
