10.3.2旋转的特征 教学课件--华师大版初中数学七年级(下)
文档属性
| 名称 | 10.3.2旋转的特征 教学课件--华师大版初中数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:32:27 | ||
图片预览






文档简介
(共15张PPT)
第 10章 轴对称、平移与旋转
10.3 旋 转
10.3.2 旋转的特征
学 习 目 标
掌握图形旋转的特征.(重点、难点)
复习导入
如图,将△ABC绕点C逆时针方向旋转,请说出:
(1)旋转中心是点____;
(2)点B的对应点是点____;
(3)CA的对应边是______;
(4)∠A的对应角是_______;
(5)点A的旋转角是∠____,
(6)点B的旋转角是∠____.
C
E
CD
∠D
ACD
BCE
思考:这些对应点、线段与角之间有什么关系呢?
知识讲解
★ 旋转的特征
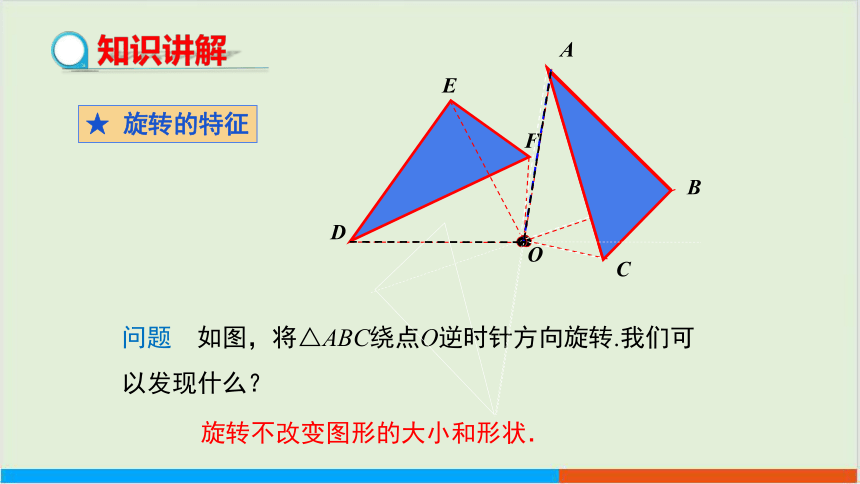
问题 如图,将△ABC绕点O逆时针方向旋转.我们可以发现什么?
旋转不改变图形的大小和形状.
D
E
A
B
F
C
O
D
E
A
B
F
C
O
(1)图中除对应线段相等
外, 还有哪些相等的线
段?
OA=OD OB=OE OC=OF
每对对应点到旋转中心的距离相等.
(2)图中除对应角相等外,还有哪些相等的角?
∠AOD=∠BOE=∠COF
旋转角彼此相等
(2)对应点到旋转中心的距离相等;
图形旋转的基本性质
(4)旋转不改变图形的大小和形状.
(1)各组对应点与旋转中心的连线所成的角相等,
都等于旋转角;
(5)旋转中心是唯一不动的点;
(3)对应线段相等,对应角相等;
例 △ ABD经过旋转后到△ ACE的位置.
(1)旋转中心是哪一点
(2)旋转了多少度 顺时针还是逆时针?
(3)如果M是AB的中点,经过上述旋转后,点M转到什么位置
A
B
C
E
M
.
解:(1)旋转中心是点A;
(2)旋转了60 °,逆时针;
(3)点M转到了AC的中点上.
D
练一练
画出下图所示的四边形 ABCD 分别以 O1,O2 为中心,
旋转角都为 30°的旋转图形.
A
B
C
D
O1
O2
A
B
C
D
O1
A′
B′
C′
D′
A
B
C
D
O2
A′
B′
D′
C′
绕 O1 顺时针旋转 30°
绕 O2 顺时针旋转 30°
拓展提升
①相同:都是一种运动;运动前后不改变图形的形状和大小.
B
A
C
O
②不同
图形变换 运动方向 运动量的衡量
平移 直线 移动一定距离
旋转 顺时针或逆时针 转动一定的角度
平移和旋转的异同:
随堂训练
A
B
C
D
E
1.如图,将Rt△ABC绕点A按顺时针方向旋转一定角度得Rt △ADE,点B的对应点D恰好落在BC边上.若AC= , ∠B=60 °,则CD的长为( )
A. 0.5 B. 1.5 C. D. 1
D
2.如图,正方形A′B′C′D′是由正方形ABCD按顺时针方向旋转45°而成的.
(1)若AB=4,则S正方形A′B′C′D′= ;
(2) ∠BAB ′= , ∠B′AD= .
(3)若连接BB′,则∠ABB′= .
16
45°
45°
67.5°
3.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,A′B′与BC交于点D,则△A′CD的面积为( )
A.1 B. C. D.2
C
课堂小结
旋转前后图形全等
线:每对对应点与旋转中心的距离相等
角:旋转角彼此相等
对应线段相等
对应角相等
旋转的特征
第 10章 轴对称、平移与旋转
10.3 旋 转
10.3.2 旋转的特征
学 习 目 标
掌握图形旋转的特征.(重点、难点)
复习导入
如图,将△ABC绕点C逆时针方向旋转,请说出:
(1)旋转中心是点____;
(2)点B的对应点是点____;
(3)CA的对应边是______;
(4)∠A的对应角是_______;
(5)点A的旋转角是∠____,
(6)点B的旋转角是∠____.
C
E
CD
∠D
ACD
BCE
思考:这些对应点、线段与角之间有什么关系呢?
知识讲解
★ 旋转的特征
问题 如图,将△ABC绕点O逆时针方向旋转.我们可以发现什么?
旋转不改变图形的大小和形状.
D
E
A
B
F
C
O
D
E
A
B
F
C
O
(1)图中除对应线段相等
外, 还有哪些相等的线
段?
OA=OD OB=OE OC=OF
每对对应点到旋转中心的距离相等.
(2)图中除对应角相等外,还有哪些相等的角?
∠AOD=∠BOE=∠COF
旋转角彼此相等
(2)对应点到旋转中心的距离相等;
图形旋转的基本性质
(4)旋转不改变图形的大小和形状.
(1)各组对应点与旋转中心的连线所成的角相等,
都等于旋转角;
(5)旋转中心是唯一不动的点;
(3)对应线段相等,对应角相等;
例 △ ABD经过旋转后到△ ACE的位置.
(1)旋转中心是哪一点
(2)旋转了多少度 顺时针还是逆时针?
(3)如果M是AB的中点,经过上述旋转后,点M转到什么位置
A
B
C
E
M
.
解:(1)旋转中心是点A;
(2)旋转了60 °,逆时针;
(3)点M转到了AC的中点上.
D
练一练
画出下图所示的四边形 ABCD 分别以 O1,O2 为中心,
旋转角都为 30°的旋转图形.
A
B
C
D
O1
O2
A
B
C
D
O1
A′
B′
C′
D′
A
B
C
D
O2
A′
B′
D′
C′
绕 O1 顺时针旋转 30°
绕 O2 顺时针旋转 30°
拓展提升
①相同:都是一种运动;运动前后不改变图形的形状和大小.
B
A
C
O
②不同
图形变换 运动方向 运动量的衡量
平移 直线 移动一定距离
旋转 顺时针或逆时针 转动一定的角度
平移和旋转的异同:
随堂训练
A
B
C
D
E
1.如图,将Rt△ABC绕点A按顺时针方向旋转一定角度得Rt △ADE,点B的对应点D恰好落在BC边上.若AC= , ∠B=60 °,则CD的长为( )
A. 0.5 B. 1.5 C. D. 1
D
2.如图,正方形A′B′C′D′是由正方形ABCD按顺时针方向旋转45°而成的.
(1)若AB=4,则S正方形A′B′C′D′= ;
(2) ∠BAB ′= , ∠B′AD= .
(3)若连接BB′,则∠ABB′= .
16
45°
45°
67.5°
3.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,A′B′与BC交于点D,则△A′CD的面积为( )
A.1 B. C. D.2
C
课堂小结
旋转前后图形全等
线:每对对应点与旋转中心的距离相等
角:旋转角彼此相等
对应线段相等
对应角相等
旋转的特征
