10.4中心对称 教学课件--华师大版初中数学七年级(下)
文档属性
| 名称 | 10.4中心对称 教学课件--华师大版初中数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:32:27 | ||
图片预览




文档简介
(共24张PPT)
第 10章 轴对称、平移与旋转
10.4 中心对称
学 习 目 标
1.理解中心对称的定义.
2.探究中心对称的性质.(难点)
3.利用中心对称的性质画中心对称图形.(重点)
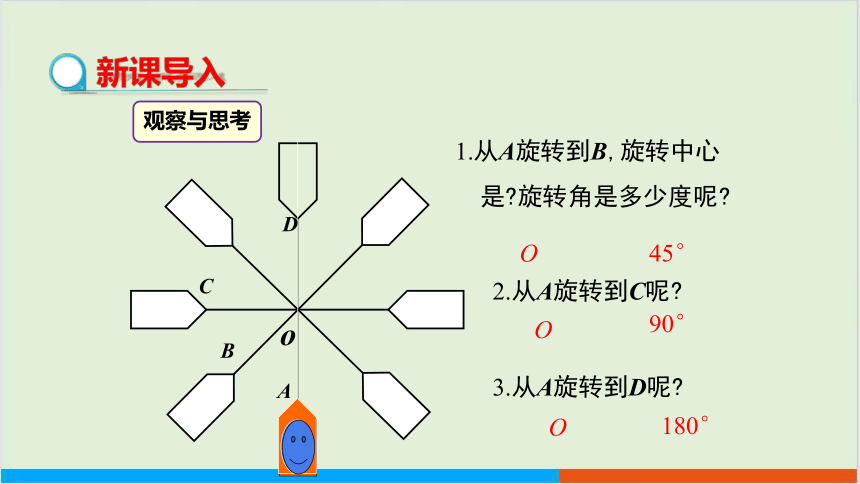
新课导入
1.从A旋转到B,旋转中心
是 旋转角是多少度呢
o
A
B
C
D
2.从A旋转到C呢
3.从A旋转到D呢
观察与思考
O
45°
O
90°
180°
O
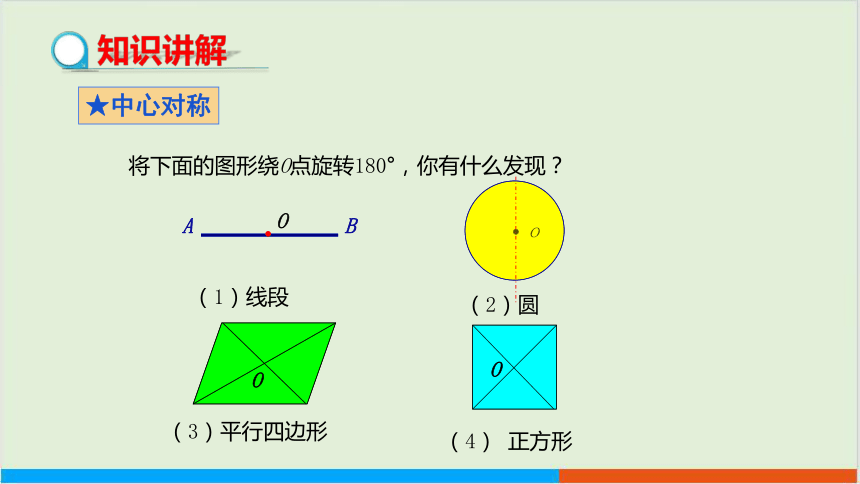
知识讲解
★中心对称
o
(2)圆
(4) 正方形
(1)线段
(3)平行四边形
A
B
将下面的图形绕O点旋转180°,你有什么发现?
O
O
O
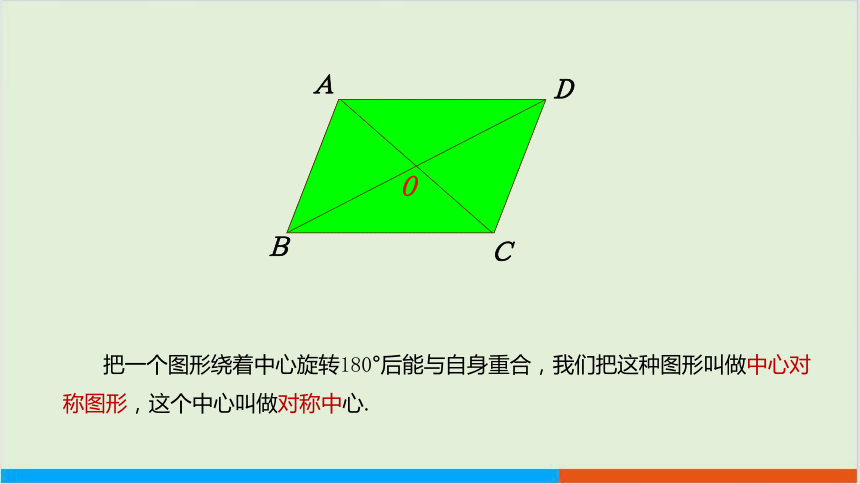
把一个图形绕着中心旋转180°后能与自身重合,我们把这种图形叫做中心对称图形,这个中心叫做对称中心.
A
B
C
D
O
问题1:如图,把其中一个图案绕点O旋转180°,你有什么发现?
答:两个图案能够完全重合在一起.
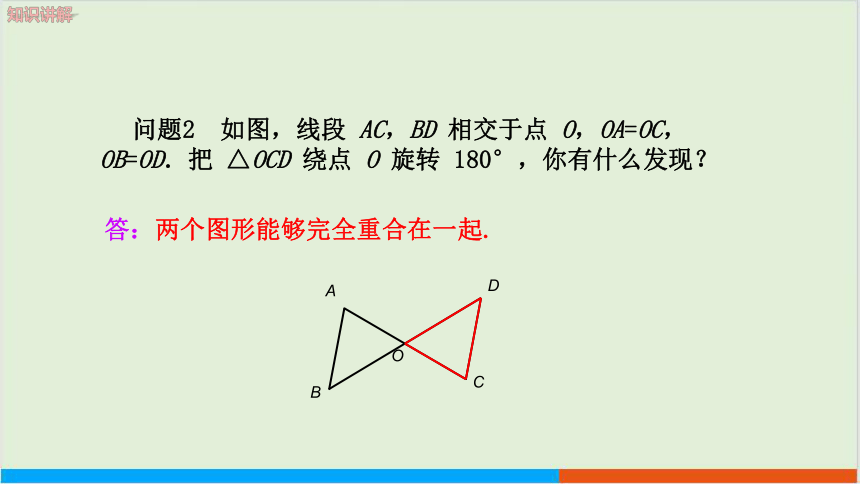
O
问题2 如图,线段 AC,BD 相交于点 O,OA=OC,OB=OD.把 △OCD 绕点 O 旋转 180°,你有什么发现?
A
B
D
C
O
答:两个图形能够完全重合在一起.
像这样,把一个图形绕某一个点旋转180 ,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称;这个点叫做对称中心;这两个图形中的对应点叫做关于中心的对称点.
中心对称与一般的旋转的联系和区别?
联系:
中心对称和一般的旋转都是绕着某一点进行旋转;
区别:
中心对称的旋转角度都是180°,一般的旋转的旋转角度不固定,中心对称是特殊的旋转.
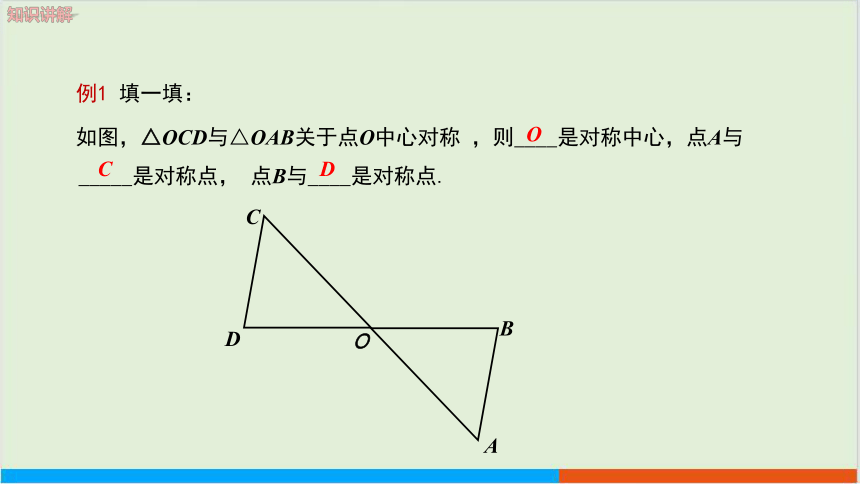
例1 填一填:
如图,△OCD与△OAB关于点O中心对称 ,则____是对称中心,点A与_____是对称点, 点B与____是对称点.
O
B
C
A
D
O
C
D
★ 中心对称的性质
找一找:
下图中△A′B′C′与△ABC关于点O是成中心对称,你能从图中找到哪些等量关系
A′
B′
C′
A
B
C
O
(1) OA=OA′,OB=OB′, OC=OC′;
(2)△ABC≌△A′B′C′.
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
中心对称的基本性质
反之,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
A
O
A'
解:第一步:连结AO;
第二步:延长AO至A',使OA'=OA;
例2 (1)已知点A和点O,画出点A关于点O的对称点A'.
则A'是所求的点.
(2)已知线段AB和点O,画出线段AB关于点O的对称线段A' B' .
B'
A'
A
B
O
解:(1)连接OA并延长至 ,使OA=O ;
(2)连接OB并延长至 ,使OB=O ;
A'
A'
B'
B'
(3)连接 .
A'
B'
(3)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
解:△A′B′C′为所求作的三角形.
A′
C′
B′
B
A
C
O
例3 如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中心O.
A
B
C
A′
B′
C′
解法1:通过观察,我们知道B、B′应是对称点,连接BB′,用刻度尺找出BB′的中点O,则点O即为所求(如图所示).
A
B
C
A′
B′
C′
O
O
解法2:通过观察,我们知道B、B′及C、C′应是两组对称点,连接BB′、CC′,相交于点O,则点O即为所求(如图所示).
A
B
C
A′
B′
C′
O
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
拓展提升
中心对称与轴对称的异同
随堂训练
1.已知下列命题:
①关于中心对称的两个图形一定不全等;
②关于中心对称的两个图形一定全等;
③两个全等的图形一定成中心对称;
其中真命题的是___________.
2.如下图所示的4组图形中,左边数字与右边数字成中心对称的
有( )
A.1组 B.2组 C.3组 D.4组
C
3.图形中的两个四边形关于某点对称,找出他们的对称中心.
o
A′
B′
C′
O
A
B
C
4.如图,已知等边△ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.
课堂小结
中心对称
概念
把一个图形绕某一个点旋转180 ,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称
性质
作图
应用1:作中心对称图形;
应用2:找出对称中心
1.中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.(即对称点与对称中心三点共线;
2.成中心对称的两个图形是全等形
第 10章 轴对称、平移与旋转
10.4 中心对称
学 习 目 标
1.理解中心对称的定义.
2.探究中心对称的性质.(难点)
3.利用中心对称的性质画中心对称图形.(重点)
新课导入
1.从A旋转到B,旋转中心
是 旋转角是多少度呢
o
A
B
C
D
2.从A旋转到C呢
3.从A旋转到D呢
观察与思考
O
45°
O
90°
180°
O
知识讲解
★中心对称
o
(2)圆
(4) 正方形
(1)线段
(3)平行四边形
A
B
将下面的图形绕O点旋转180°,你有什么发现?
O
O
O
把一个图形绕着中心旋转180°后能与自身重合,我们把这种图形叫做中心对称图形,这个中心叫做对称中心.
A
B
C
D
O
问题1:如图,把其中一个图案绕点O旋转180°,你有什么发现?
答:两个图案能够完全重合在一起.
O
问题2 如图,线段 AC,BD 相交于点 O,OA=OC,OB=OD.把 △OCD 绕点 O 旋转 180°,你有什么发现?
A
B
D
C
O
答:两个图形能够完全重合在一起.
像这样,把一个图形绕某一个点旋转180 ,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称;这个点叫做对称中心;这两个图形中的对应点叫做关于中心的对称点.
中心对称与一般的旋转的联系和区别?
联系:
中心对称和一般的旋转都是绕着某一点进行旋转;
区别:
中心对称的旋转角度都是180°,一般的旋转的旋转角度不固定,中心对称是特殊的旋转.
例1 填一填:
如图,△OCD与△OAB关于点O中心对称 ,则____是对称中心,点A与_____是对称点, 点B与____是对称点.
O
B
C
A
D
O
C
D
★ 中心对称的性质
找一找:
下图中△A′B′C′与△ABC关于点O是成中心对称,你能从图中找到哪些等量关系
A′
B′
C′
A
B
C
O
(1) OA=OA′,OB=OB′, OC=OC′;
(2)△ABC≌△A′B′C′.
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
中心对称的基本性质
反之,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
A
O
A'
解:第一步:连结AO;
第二步:延长AO至A',使OA'=OA;
例2 (1)已知点A和点O,画出点A关于点O的对称点A'.
则A'是所求的点.
(2)已知线段AB和点O,画出线段AB关于点O的对称线段A' B' .
B'
A'
A
B
O
解:(1)连接OA并延长至 ,使OA=O ;
(2)连接OB并延长至 ,使OB=O ;
A'
A'
B'
B'
(3)连接 .
A'
B'
(3)如图,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.
解:△A′B′C′为所求作的三角形.
A′
C′
B′
B
A
C
O
例3 如图,已知△ABC与△A′B′C′中心对称,找出它们的对称中心O.
A
B
C
A′
B′
C′
解法1:通过观察,我们知道B、B′应是对称点,连接BB′,用刻度尺找出BB′的中点O,则点O即为所求(如图所示).
A
B
C
A′
B′
C′
O
O
解法2:通过观察,我们知道B、B′及C、C′应是两组对称点,连接BB′、CC′,相交于点O,则点O即为所求(如图所示).
A
B
C
A′
B′
C′
O
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
拓展提升
中心对称与轴对称的异同
随堂训练
1.已知下列命题:
①关于中心对称的两个图形一定不全等;
②关于中心对称的两个图形一定全等;
③两个全等的图形一定成中心对称;
其中真命题的是___________.
2.如下图所示的4组图形中,左边数字与右边数字成中心对称的
有( )
A.1组 B.2组 C.3组 D.4组
C
3.图形中的两个四边形关于某点对称,找出他们的对称中心.
o
A′
B′
C′
O
A
B
C
4.如图,已知等边△ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.
课堂小结
中心对称
概念
把一个图形绕某一个点旋转180 ,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称
性质
作图
应用1:作中心对称图形;
应用2:找出对称中心
1.中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.(即对称点与对称中心三点共线;
2.成中心对称的两个图形是全等形
