10.5图形的全等 教学课件--华师大版初中数学七年级(下)
文档属性
| 名称 | 10.5图形的全等 教学课件--华师大版初中数学七年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:32:27 | ||
图片预览




文档简介
(共20张PPT)
第 10章 轴对称、平移与旋转
10.5 图形的全等
学 习 目 标
1.理解全等图形的定义.
2.探究全等图形的性质与判定.(难点)
3.从全等图形的判定到全等三角形的判定.(重点)
新课导入
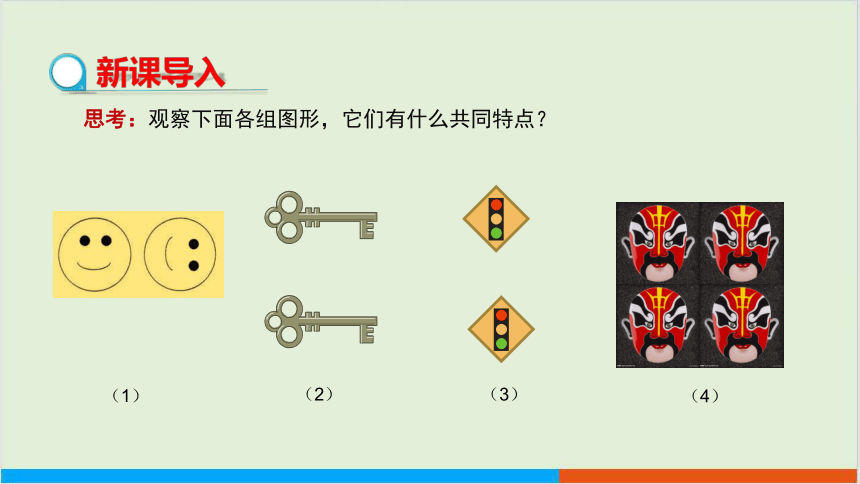
思考:观察下面各组图形,它们有什么共同特点?
(1)
(2)
(3)
(4)
都有形状、大小相同的图片
(5)
(6)
(7)
你能再举出一些类似的例子吗
知识讲解
★全等图形的概念
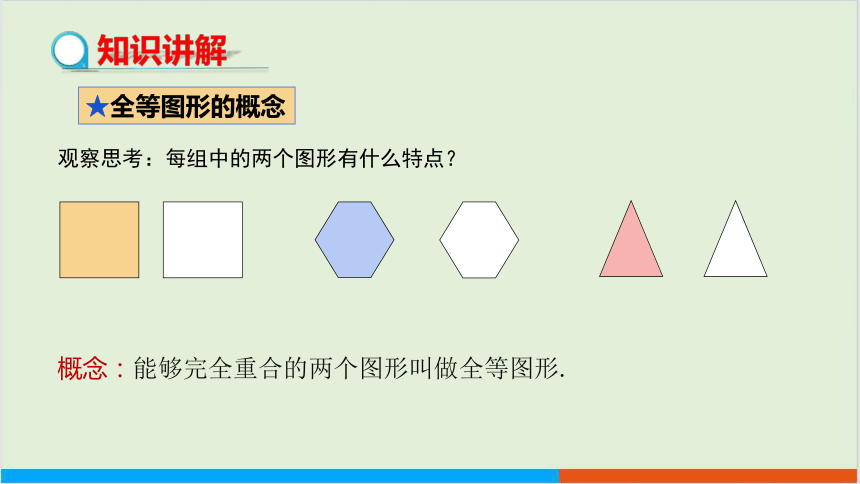
观察思考:每组中的两个图形有什么特点?
概念:能够完全重合的两个图形叫做全等图形.
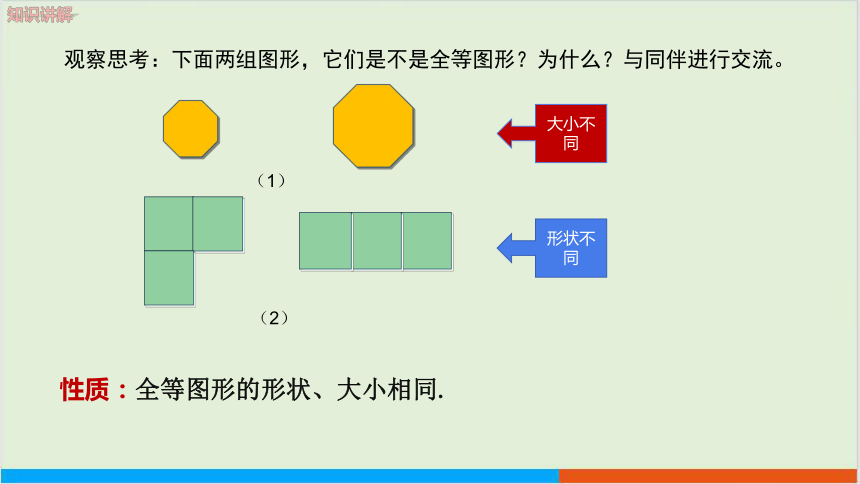
观察思考:下面两组图形,它们是不是全等图形?为什么?与同伴进行交流。
(1)
(2)
大小不同
形状不同
性质:全等图形的形状、大小相同.
A
A
C
B
D
E
A
B
D
C
A
B
C
D
B
C
N
M
F
E
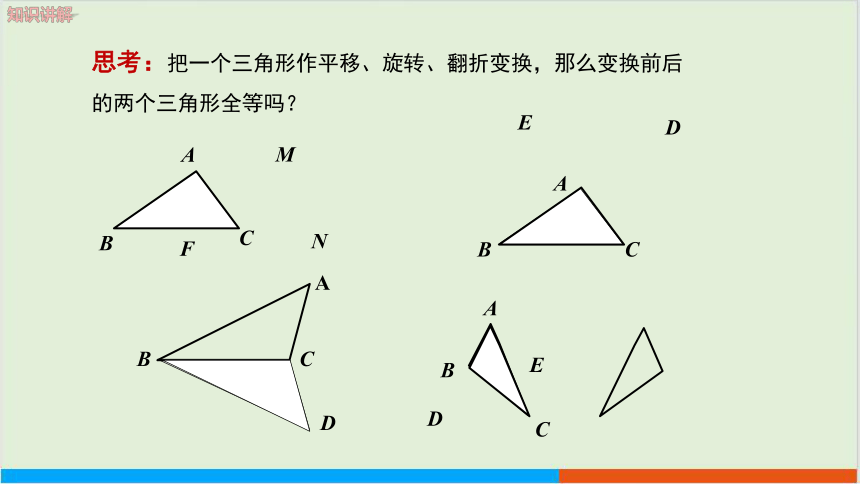
思考:把一个三角形作平移、旋转、翻折变换,那么变换前后的两个三角形全等吗?
全等变化: 一个图形经过平移、翻折、旋转后,位置 变化了,但形状和大小都没有改变,即平移、翻折、旋转前后的两个图形全等.
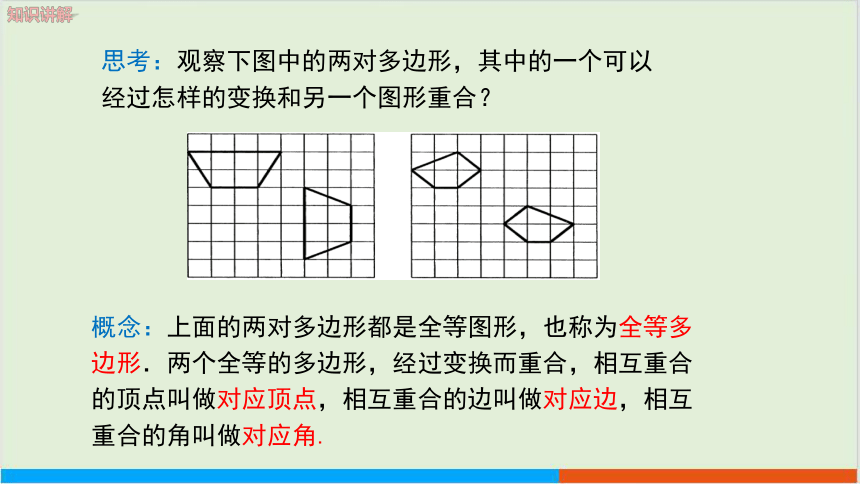
思考:观察下图中的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合?
概念:上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
★ 全等图形的性质
A
B
C
D
E
A1
B1
C1
D1
E1
五边形ABCDE 五边形A1B1C1D1E1
对应边
试一试 找出下面全等多边形的等量关系
AB A1B1
BC B1C1
CD C1D1
DE D1E1
EA E1A1
=
=
=
=
=
对应角
∠A ∠A1
∠B ∠B1
∠D =∠D1
∠E ∠E1
=
=
=
∠C=∠C'
此符号表示全等,读作“全等于”.
全等多边形的性质:
全等多边形的对应边、对应角分别相等.
全等多边形的判定方法:
如果两个多边形的边、角分别对应相等,那么这两个多边形全等.
全等三角形的性质:
全等三角形的对应边、对应角分别相等.
全等三角形的判定方法:
如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
例1 如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
解:△BOD与△COE的对应边为:
BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:
∠DAO与∠EAO,∠ADO与∠AEO,∠AOD与∠AOE.
对应元素的确定方法:
(1)图形特征法:
① 最长边对最长边,最短边对最短边.
②最大角对最大角,最小角对最小角.
(2)位置关系法:
①公共角(对顶角)为对应角,公共边为对应边.
②对应角的对边为对应边,两个对应角所夹的边是对应边.
③对应边的对角为对应角,两条对应边所夹的角是对应角.
(3)字母顺序法:
根据书写规范按照对应顶点确定对应边和对应角.
例2 如图,,,,,求的度数和的长.
分析:根据全等三角形对应边、对应角相等求的度数和CF的长.
解:∵△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,
∴CF=BC-BF=7-4=3.
随堂训练
1.⑴已知:如图1,△与△全等,请用式子表示出这种关系:________________
⑵找出对应边,它们有什么关系?
对应边:_______ ______ _______
⑶找出对应角,它们有什么关系?
对应角:________ _________ ______________
⑷如果∠=35°,∠75°,那么∠ ____.
图1
≌
70°
和
和
和
=
=
=
∠
∠
∠
∠
∠
∠
和
和
和
2.如图,如果△≌ △,
那么吗?
平行
7cm
5cm
)39°
3.如图,矩形沿折叠,使点落在上 的点处,如果cm,5cm,则___cm,cm,
7
5
12°
4.如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
解:(1)对应边有EF和NM,FG和MH,EG和NH;
对应角有∠E和∠N, ∠F和∠M, ∠和∠NHM.
(2)求线段NM 及HG 的长度;
(3)观察图形中对应线段的数量或位置关系,试提出一个正确的结论并证明.
解:因为 △EFG≌△NMH,
所以NM=EF=2.1cm,
EG=NH=3.3cm.
所以HG=EG –EH =3.3-1.1=2.2(cm).
解:结论:EF∥NM
证明: 因为 △EFG≌△NMH,
所以 ∠E=∠N. 所以 EF∥NM.
想一想:你还能得出其他结论吗?
课堂小结
全等图形
概念
对应点、对应角、对应边
性质
对应角相等,对应边相等
全等三角形
性质:对应边、角分别相等.
判定方法:边、角分别对应相等,则三角形全等.
第 10章 轴对称、平移与旋转
10.5 图形的全等
学 习 目 标
1.理解全等图形的定义.
2.探究全等图形的性质与判定.(难点)
3.从全等图形的判定到全等三角形的判定.(重点)
新课导入
思考:观察下面各组图形,它们有什么共同特点?
(1)
(2)
(3)
(4)
都有形状、大小相同的图片
(5)
(6)
(7)
你能再举出一些类似的例子吗
知识讲解
★全等图形的概念
观察思考:每组中的两个图形有什么特点?
概念:能够完全重合的两个图形叫做全等图形.
观察思考:下面两组图形,它们是不是全等图形?为什么?与同伴进行交流。
(1)
(2)
大小不同
形状不同
性质:全等图形的形状、大小相同.
A
A
C
B
D
E
A
B
D
C
A
B
C
D
B
C
N
M
F
E
思考:把一个三角形作平移、旋转、翻折变换,那么变换前后的两个三角形全等吗?
全等变化: 一个图形经过平移、翻折、旋转后,位置 变化了,但形状和大小都没有改变,即平移、翻折、旋转前后的两个图形全等.
思考:观察下图中的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合?
概念:上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
★ 全等图形的性质
A
B
C
D
E
A1
B1
C1
D1
E1
五边形ABCDE 五边形A1B1C1D1E1
对应边
试一试 找出下面全等多边形的等量关系
AB A1B1
BC B1C1
CD C1D1
DE D1E1
EA E1A1
=
=
=
=
=
对应角
∠A ∠A1
∠B ∠B1
∠D =∠D1
∠E ∠E1
=
=
=
∠C=∠C'
此符号表示全等,读作“全等于”.
全等多边形的性质:
全等多边形的对应边、对应角分别相等.
全等多边形的判定方法:
如果两个多边形的边、角分别对应相等,那么这两个多边形全等.
全等三角形的性质:
全等三角形的对应边、对应角分别相等.
全等三角形的判定方法:
如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
例1 如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
解:△BOD与△COE的对应边为:
BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:
∠DAO与∠EAO,∠ADO与∠AEO,∠AOD与∠AOE.
对应元素的确定方法:
(1)图形特征法:
① 最长边对最长边,最短边对最短边.
②最大角对最大角,最小角对最小角.
(2)位置关系法:
①公共角(对顶角)为对应角,公共边为对应边.
②对应角的对边为对应边,两个对应角所夹的边是对应边.
③对应边的对角为对应角,两条对应边所夹的角是对应角.
(3)字母顺序法:
根据书写规范按照对应顶点确定对应边和对应角.
例2 如图,,,,,求的度数和的长.
分析:根据全等三角形对应边、对应角相等求的度数和CF的长.
解:∵△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,
∴CF=BC-BF=7-4=3.
随堂训练
1.⑴已知:如图1,△与△全等,请用式子表示出这种关系:________________
⑵找出对应边,它们有什么关系?
对应边:_______ ______ _______
⑶找出对应角,它们有什么关系?
对应角:________ _________ ______________
⑷如果∠=35°,∠75°,那么∠ ____.
图1
≌
70°
和
和
和
=
=
=
∠
∠
∠
∠
∠
∠
和
和
和
2.如图,如果△≌ △,
那么吗?
平行
7cm
5cm
)39°
3.如图,矩形沿折叠,使点落在上 的点处,如果cm,5cm,则___cm,cm,
7
5
12°
4.如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
解:(1)对应边有EF和NM,FG和MH,EG和NH;
对应角有∠E和∠N, ∠F和∠M, ∠和∠NHM.
(2)求线段NM 及HG 的长度;
(3)观察图形中对应线段的数量或位置关系,试提出一个正确的结论并证明.
解:因为 △EFG≌△NMH,
所以NM=EF=2.1cm,
EG=NH=3.3cm.
所以HG=EG –EH =3.3-1.1=2.2(cm).
解:结论:EF∥NM
证明: 因为 △EFG≌△NMH,
所以 ∠E=∠N. 所以 EF∥NM.
想一想:你还能得出其他结论吗?
课堂小结
全等图形
概念
对应点、对应角、对应边
性质
对应角相等,对应边相等
全等三角形
性质:对应边、角分别相等.
判定方法:边、角分别对应相等,则三角形全等.
