6.2.2解一元一次方程(第1课时去括号解一元一次方程) 教学课件--华师大版初中数学七年级(下)
文档属性
| 名称 | 6.2.2解一元一次方程(第1课时去括号解一元一次方程) 教学课件--华师大版初中数学七年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 597.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:32:27 | ||
图片预览






文档简介
(共19张PPT)
6.2.2 解一元一次方程
第 6章 一元一次方程
第1课时 去括号解一元一次方程
第6章 一元一次方程
学 习 目 标
1.理解一元一次方程的概念及特点.(重点)
2. 了解“去括号”是解方程的重要步骤;
3.准确而熟练地运用去括号法则解带有括号的方
程.(难点、重点)
温故知新
1.化简下列各式:
(1) (-3a+2b) +3(a-b);
(2) -5+4-(-3+ ).
解: (1) 原式;
(2) 原式.
去括号法则
去掉“+ ( )”,括号内各项的符号不变. a + (b + c) =a + b + c.
去掉“– ( )”,括号内各项的符号改变. a -(b + c) =a -b - c.
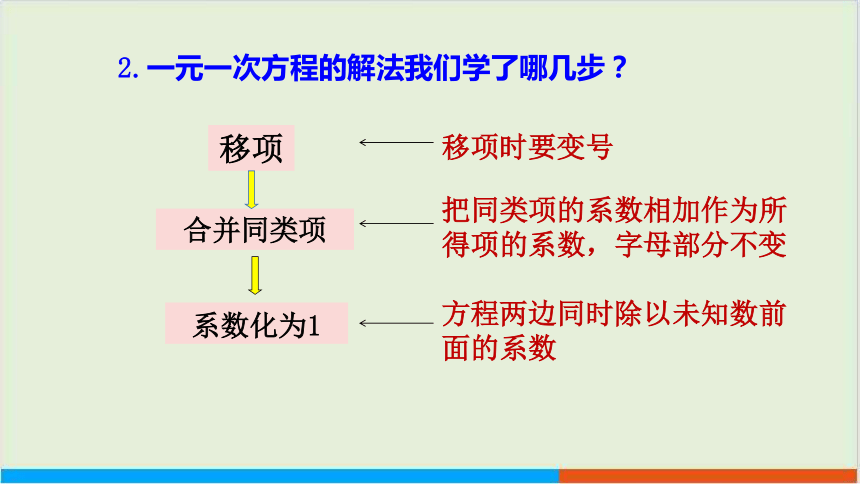
2.一元一次方程的解法我们学了哪几步?
移项
合并同类项
系数化为1
移项时要变号
把同类项的系数相加作为所
得项的系数,字母部分不变
方程两边同时除以未知数前
面的系数
知识讲解
问题 观察以下两个方程有什么共同特点
只含有一个未知数,
(一元)
(一次)
未知数的次数都是1,
等号两边都是整式,
这样的方程叫做一元一次方程.
我们发现 ,
1.一元一次方程的概念
一元一次方程定义:
只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做一元一次方程.
注意以下三点:
(1)一元一次方程有如下特点:①只含有一个未知数;
②未知数的次数是1;③含有未知数的式子是整式.
(2)一元一次方程的最简形式为:ax=b(a≠0).
(3)一元一次方程的标准形式为:ax+b= 0
(其中x是未知数,a、b是已知数,并且a≠0).
下列哪些是一元一次方程?
(1) ; (2) ;
(3) ;(4) ;
(5) ;(6) .
(7)
练一练
√
√
去括号法则:
去掉“+( )”,括号内各项的符号不变.
去掉“–( )”,括号内各项的符号改变.
用三个字母a、b、c表示去括号前后的变化规律:
a+(b+c)
a–(b+c)
= a+b+c
= a–b–c
2.去括号解一元一次方程
解方程:3(x-2)+1=x-(2x-1)
3x-6+1=x-2x+1,
解:原方程的两边分别去括号,得
即 3x-5=-x+1
移项,得 3x+x=1+5
即 4x=6
两边都除以4,得
例1
解:(1)去括号,得
系数化为1,得
解下列方程:
;
例2
合并同类项,得
移项,得
8.
解:(1)去括号,得
系数化为1,得
.
合并同类项,得
移项,得
.
通过以上解方程的过程,你能总结出解含有括号的一元一次方程的一般步骤吗?
去括号
移项
合并同类项
系数化为1
方程中有带括号的式子时,去括号是常用的化简步骤.
解方程:(1).
解:去括号,得
.
移项,得
.
合并同类项,得
.
系数化为1,得
.
针对训练
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
1.若关于x的方程 3x + ( 2a+1 ) = x-( 3a+2 ) 的解为x = 0,
则a的值等于 ( )
A. B. C. D.
随堂训练
D
2.当x= 时,代数式2(x2-1)-x2的值比代数式 x2+3x
-2的值大6.
-2
3.下列变形对吗?若不对,请说明理由,并改正.
解方程
去括号,得
移项,得
合并同类项,得5;
两边同除以-0.2得
去括号变形错,有一项
没变号,改正如下:
去括号,得
移项,得
合并同类项,得
解得
4. 解下列方程:
解:
(1)
(2).
课堂小结
解一元一次方程的步骤
去括号
移项
合并同类项
系数化为1
6.2.2 解一元一次方程
第 6章 一元一次方程
第1课时 去括号解一元一次方程
第6章 一元一次方程
学 习 目 标
1.理解一元一次方程的概念及特点.(重点)
2. 了解“去括号”是解方程的重要步骤;
3.准确而熟练地运用去括号法则解带有括号的方
程.(难点、重点)
温故知新
1.化简下列各式:
(1) (-3a+2b) +3(a-b);
(2) -5+4-(-3+ ).
解: (1) 原式;
(2) 原式.
去括号法则
去掉“+ ( )”,括号内各项的符号不变. a + (b + c) =a + b + c.
去掉“– ( )”,括号内各项的符号改变. a -(b + c) =a -b - c.
2.一元一次方程的解法我们学了哪几步?
移项
合并同类项
系数化为1
移项时要变号
把同类项的系数相加作为所
得项的系数,字母部分不变
方程两边同时除以未知数前
面的系数
知识讲解
问题 观察以下两个方程有什么共同特点
只含有一个未知数,
(一元)
(一次)
未知数的次数都是1,
等号两边都是整式,
这样的方程叫做一元一次方程.
我们发现 ,
1.一元一次方程的概念
一元一次方程定义:
只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做一元一次方程.
注意以下三点:
(1)一元一次方程有如下特点:①只含有一个未知数;
②未知数的次数是1;③含有未知数的式子是整式.
(2)一元一次方程的最简形式为:ax=b(a≠0).
(3)一元一次方程的标准形式为:ax+b= 0
(其中x是未知数,a、b是已知数,并且a≠0).
下列哪些是一元一次方程?
(1) ; (2) ;
(3) ;(4) ;
(5) ;(6) .
(7)
练一练
√
√
去括号法则:
去掉“+( )”,括号内各项的符号不变.
去掉“–( )”,括号内各项的符号改变.
用三个字母a、b、c表示去括号前后的变化规律:
a+(b+c)
a–(b+c)
= a+b+c
= a–b–c
2.去括号解一元一次方程
解方程:3(x-2)+1=x-(2x-1)
3x-6+1=x-2x+1,
解:原方程的两边分别去括号,得
即 3x-5=-x+1
移项,得 3x+x=1+5
即 4x=6
两边都除以4,得
例1
解:(1)去括号,得
系数化为1,得
解下列方程:
;
例2
合并同类项,得
移项,得
8.
解:(1)去括号,得
系数化为1,得
.
合并同类项,得
移项,得
.
通过以上解方程的过程,你能总结出解含有括号的一元一次方程的一般步骤吗?
去括号
移项
合并同类项
系数化为1
方程中有带括号的式子时,去括号是常用的化简步骤.
解方程:(1).
解:去括号,得
.
移项,得
.
合并同类项,得
.
系数化为1,得
.
针对训练
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
1.若关于x的方程 3x + ( 2a+1 ) = x-( 3a+2 ) 的解为x = 0,
则a的值等于 ( )
A. B. C. D.
随堂训练
D
2.当x= 时,代数式2(x2-1)-x2的值比代数式 x2+3x
-2的值大6.
-2
3.下列变形对吗?若不对,请说明理由,并改正.
解方程
去括号,得
移项,得
合并同类项,得5;
两边同除以-0.2得
去括号变形错,有一项
没变号,改正如下:
去括号,得
移项,得
合并同类项,得
解得
4. 解下列方程:
解:
(1)
(2).
课堂小结
解一元一次方程的步骤
去括号
移项
合并同类项
系数化为1
