8.2.2不等式的简单变形 教学课件--华师大版初中数学七年级(下)
文档属性
| 名称 | 8.2.2不等式的简单变形 教学课件--华师大版初中数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:32:27 | ||
图片预览










文档简介
(共31张PPT)
8.2.2 不等式的简单变形
第 8章 一元一次不等式
学 习 目 标
理解并掌握不等式的基本性质; (重点)
会用不等式的基本性质解简单的不等式.(重点、难点)
1
2
前面我们已经学习过等式的基本性质
(1)等式两边加(或减去)同一个数(或式子),
结果仍相等.
(2)等式两边乘同一个数,或除以同一个不为0的数,
结果仍相等.
猜想 :不等式也具有同样的性质吗?
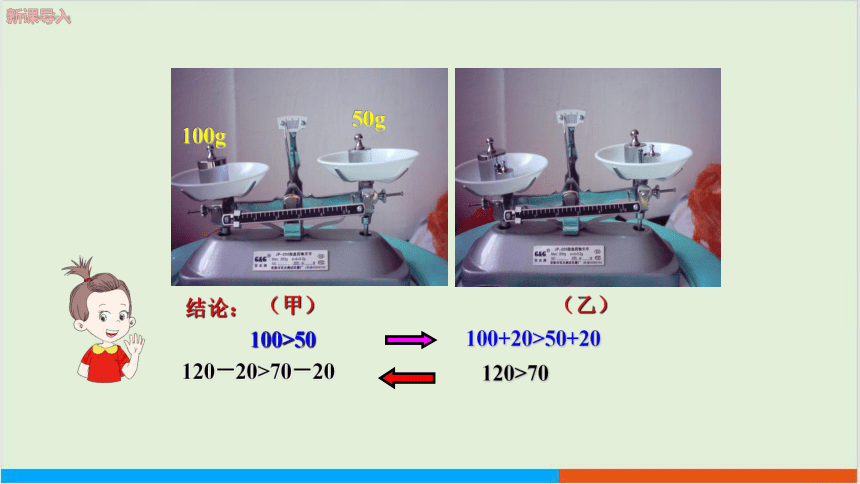
新课导入
(甲)
(乙)
100g
50g
结论:
100>50
100+20>50+20
120>70
120-20>70-20
新课导入
不等式的性质1
知 识 讲 解
(1)5>3, 5+2___3+2 , 5-2___3-2 ;
(2)-1<3, -1+2___3+2 , -1-3___3-3 ;
根据发现的规律填空:当不等式两边加(或减)同一个数(正数或负数)时,不等号的方向______.
不变
﹥
﹥
﹤
﹤
思考:用“﹥”或“﹤”填空,你发现其中的什么规律:
发现:
+ C
-C
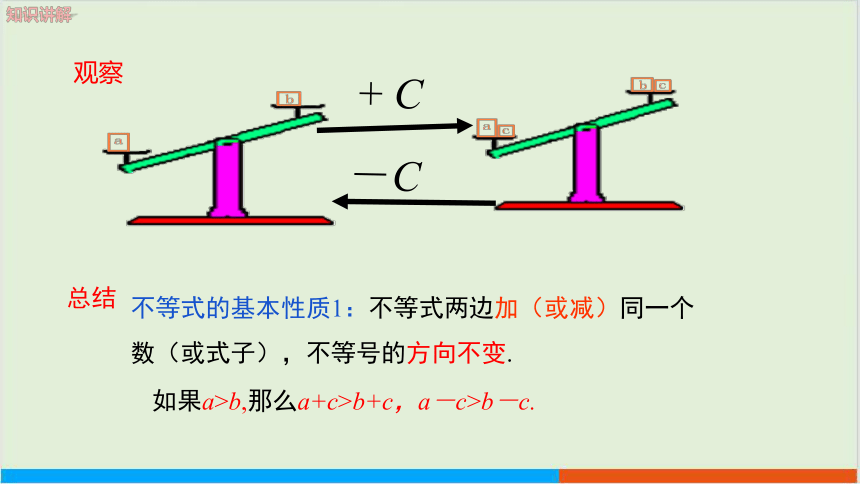
不等式的基本性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a+c>b+c,a-c>b-c.
观察
总结
知识讲解
解: 因为 a>b,两边都加上3,
解: 因为 a由不等式基本性质1,得
a+3 > b+3;
由不等式基本性质1,得
a-5 < b-5 .
(1)已知 a>b,则a+3 b+3
(2)已知 a>
<
用“>”或“<”填空:
例1
知识讲解
用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+3>6,则x______3,
根据__________________;
(2)若a-2<3,则a______5,
根据__________________.
>
<
不等式的基本性质1
不等式的基本性质1
练一练
知识讲解
不等式的基本性质2、3
问题1 已知苹果的价格是a元/kg,梨的价格是b元/kg,且a > b. 小李各买了3kg苹果和梨,则买哪种水果花钱较多?
用不等号填空: 3a 3b.
问题2 在某次知识抢答赛中,甲、乙两队的总得分分别为a,b,其中a>b. 已知每队人员均为3名,则哪队的平均得分高?
用不等号填空:
a÷3 b÷3.
>
>
知识讲解
用不等号填一填:
1.a b ;
2.2a 2b;
3. .
如图所示,托盘天平的右盘放上一质量为bg的立体木块,
左盘放上一质量为ag的立体木块,天平向左倾斜.
ag
bg
>
>
>
ag
bg
你发现了什么?
问题3
知识讲解
即,如果a > b,c > 0,那么 ac > bc, > .
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
发现
不等式的基本性质2 不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
总结
知识讲解
a>b
-a-b
a-a-b>b-a-b
-b>-a
(-1)×a<(-1)×b
×(-1)
不等式两边同乘以-1,不等号方向改变.
猜想 不等式两边同乘以一个负数,不等号方向改变.
a>b
×(-1)
-a<-b
×3
-3a<-3b
×c(c>0)
-ac<-bc
×-c(-c<0)
探究
知识讲解
即,如果a > b,c < 0,那么 ac < bc, .
总结
不等式的基本性质3 不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
知识讲解
因为 a>b,两边都乘3,
因为 a>b,两边都乘-1,
解:
由不等式基本性质2,得
3a > 3b.
由不等式基本性质3,得
-a < -b.
(1)已知 a>b,则3a 3b ;
(2)已知 a>b,则-a -b .
>
<
用“>”或“<”填空:
解:
例2
知识讲解
因为 a由不等式基本性质3,得
由不等式基本性质1,得
(3)已知 a>
因为 ,两边都加2,
解析:
知识讲解
1.设a>b,用“<”“>”填空并回答是根据不等
式的哪一条基本性质.
(1) a - 7____b - 7;
(2) a÷6____b÷6
(3) 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数)
>
>
>
>
>
<
不等式的基本性质1
不等式的基本性质2
不等式的基本性质2
不等式的基本性质3
不等式的基本性质1,2
不等式的基本性质2
练一练
知识讲解
2.已知a<0,用“<”“>”填空:
(1)a+2 ____2; (2)a-1 _____-1;
(3)3a______0; (4) ______0;
(5)a2_____0; (6)a3______0;
(7)a-1_____0; (8)|a|______0.
<
<
<
>
<
>
<
>
知识讲解
思考 等式有对称性及传递性,那么不等式具有对
称性和传递性吗
已知x>5,那么5由8如:8<10,10<15 ,8 15.
x>5 5<
性质4(对称性):如果a>b,那么b性质5(同向传递性):如果a>b,b>c,那么a>c.
知识讲解
如果不等式 (a+1)x<a+1可变形为 x>1,
那么a 必须满足________.
方法总结:只有当不等式的两边都乘(或除以)一个负数时,
不等号的方向才改变.
解析:根据不等式的基本性质可判断,a+1为负数,
即a+1<0,可得 a<-1.
a<-1
例3
知识讲解
利用不等式的性质解下列不等式:
解未知数为x的不等式
化为x>a或x﹤a的形式
目标
方法:不等式基本性质1~3
利用不等式的性质解简单的不等式
解题思路:
例4
知识讲解
(1)x -7 < 8 ;
(2) 3x < 2x -3 .
知识讲解
(1) x -7 < 8,
解:
不等式的两边都加上7,由不等式基本性质1,得
x -7+7 < 8+7,
根据不等式基本性质1
即 x < 15 .
知识讲解
(2) 3x < 2x -3,
不等式的两边都减去2x,由不等式基本性质1,得
3x -2x < 2x-3-2x,
根据不等式基本性质1
即 x < -3.
知识讲解
由(2)可以看出,运用不等式基本性质1 对 3x < 2x-3 进行化简的过程,就是对不等式3x< 2x-3 作了如下变形:
(2) 3x < 2x -3
3x < 2x -3
3x
<
2x
-
3
-
从变形前后的两个不等式可以看出,这种变形就是把不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.
例5 解下列不等式: (1) >50; (2) -4x>3.
为了使不等式>50中不等号的一边变为x,根据
不等式的基本性质2,不等式的两边都除以,不等号
的方向不变,得
x﹥75.
这个不等式的解集在数轴上的表示如图所示:
0
75
解:(1) >50;
知识讲解
为了使不等式-4x﹥3中的不等号的一边变为x,
根据__________________,不等式两边都除以____,
不等号的方向______,得
x﹤- .
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
不等式的基本性质3
-4
改变
(2) -4x>3.
知识讲解
1. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b-10 a -10 .
<
>
x < 2
x < 6
2. 把下列不等式化为x>a或x(1)5>3+x;
(2)2x<x+6.
随 堂 训 练
3.由x<y得到ax<ay,则a应满足条件是( )
A.a≥0 B.a≤0
C.a>0 D.a<0
C
4.已知实数ab若a>b则下列结果正确的是( )
A.a5C.< D.3a>3b
D
随堂训练
5.若x>y则下列式子错误的是( )
A.x3>y3
B.3x> 3 y
C.x3>y3
D.>
B
随堂训练
6.利用不等式的性质解下列不等式,并在数轴上表示其解集.
(2)-2x > 3
(1)x-5 > -1
(3)7x < 6x-6
x>4
x<-6
4
0
0
0
-6
x<-
随堂训练
不等式的基本性质
不等式的基本性质2
不等式的基本性质3
→
→
如
那么
如果
那么
应用性质对不等式简单变形
不等式的
基本性质1
如果a>b,那么a+c>b+c,
a-c>b-c
→
课 堂 小 结
8.2.2 不等式的简单变形
第 8章 一元一次不等式
学 习 目 标
理解并掌握不等式的基本性质; (重点)
会用不等式的基本性质解简单的不等式.(重点、难点)
1
2
前面我们已经学习过等式的基本性质
(1)等式两边加(或减去)同一个数(或式子),
结果仍相等.
(2)等式两边乘同一个数,或除以同一个不为0的数,
结果仍相等.
猜想 :不等式也具有同样的性质吗?
新课导入
(甲)
(乙)
100g
50g
结论:
100>50
100+20>50+20
120>70
120-20>70-20
新课导入
不等式的性质1
知 识 讲 解
(1)5>3, 5+2___3+2 , 5-2___3-2 ;
(2)-1<3, -1+2___3+2 , -1-3___3-3 ;
根据发现的规律填空:当不等式两边加(或减)同一个数(正数或负数)时,不等号的方向______.
不变
﹥
﹥
﹤
﹤
思考:用“﹥”或“﹤”填空,你发现其中的什么规律:
发现:
+ C
-C
不等式的基本性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a+c>b+c,a-c>b-c.
观察
总结
知识讲解
解: 因为 a>b,两边都加上3,
解: 因为 a
a+3 > b+3;
由不等式基本性质1,得
a-5 < b-5 .
(1)已知 a>b,则a+3 b+3
(2)已知 a
<
用“>”或“<”填空:
例1
知识讲解
用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+3>6,则x______3,
根据__________________;
(2)若a-2<3,则a______5,
根据__________________.
>
<
不等式的基本性质1
不等式的基本性质1
练一练
知识讲解
不等式的基本性质2、3
问题1 已知苹果的价格是a元/kg,梨的价格是b元/kg,且a > b. 小李各买了3kg苹果和梨,则买哪种水果花钱较多?
用不等号填空: 3a 3b.
问题2 在某次知识抢答赛中,甲、乙两队的总得分分别为a,b,其中a>b. 已知每队人员均为3名,则哪队的平均得分高?
用不等号填空:
a÷3 b÷3.
>
>
知识讲解
用不等号填一填:
1.a b ;
2.2a 2b;
3. .
如图所示,托盘天平的右盘放上一质量为bg的立体木块,
左盘放上一质量为ag的立体木块,天平向左倾斜.
ag
bg
>
>
>
ag
bg
你发现了什么?
问题3
知识讲解
即,如果a > b,c > 0,那么 ac > bc, > .
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
发现
不等式的基本性质2 不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
总结
知识讲解
a>b
-a-b
a-a-b>b-a-b
-b>-a
(-1)×a<(-1)×b
×(-1)
不等式两边同乘以-1,不等号方向改变.
猜想 不等式两边同乘以一个负数,不等号方向改变.
a>b
×(-1)
-a<-b
×3
-3a<-3b
×c(c>0)
-ac<-bc
×-c(-c<0)
探究
知识讲解
即,如果a > b,c < 0,那么 ac < bc, .
总结
不等式的基本性质3 不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
知识讲解
因为 a>b,两边都乘3,
因为 a>b,两边都乘-1,
解:
由不等式基本性质2,得
3a > 3b.
由不等式基本性质3,得
-a < -b.
(1)已知 a>b,则3a 3b ;
(2)已知 a>b,则-a -b .
>
<
用“>”或“<”填空:
解:
例2
知识讲解
因为 a
由不等式基本性质1,得
(3)已知 a
因为 ,两边都加2,
解析:
知识讲解
1.设a>b,用“<”“>”填空并回答是根据不等
式的哪一条基本性质.
(1) a - 7____b - 7;
(2) a÷6____b÷6
(3) 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数)
>
>
>
>
>
<
不等式的基本性质1
不等式的基本性质2
不等式的基本性质2
不等式的基本性质3
不等式的基本性质1,2
不等式的基本性质2
练一练
知识讲解
2.已知a<0,用“<”“>”填空:
(1)a+2 ____2; (2)a-1 _____-1;
(3)3a______0; (4) ______0;
(5)a2_____0; (6)a3______0;
(7)a-1_____0; (8)|a|______0.
<
<
<
>
<
>
<
>
知识讲解
思考 等式有对称性及传递性,那么不等式具有对
称性和传递性吗
已知x>5,那么5
x>5 5
性质4(对称性):如果a>b,那么b
知识讲解
如果不等式 (a+1)x<a+1可变形为 x>1,
那么a 必须满足________.
方法总结:只有当不等式的两边都乘(或除以)一个负数时,
不等号的方向才改变.
解析:根据不等式的基本性质可判断,a+1为负数,
即a+1<0,可得 a<-1.
a<-1
例3
知识讲解
利用不等式的性质解下列不等式:
解未知数为x的不等式
化为x>a或x﹤a的形式
目标
方法:不等式基本性质1~3
利用不等式的性质解简单的不等式
解题思路:
例4
知识讲解
(1)x -7 < 8 ;
(2) 3x < 2x -3 .
知识讲解
(1) x -7 < 8,
解:
不等式的两边都加上7,由不等式基本性质1,得
x -7+7 < 8+7,
根据不等式基本性质1
即 x < 15 .
知识讲解
(2) 3x < 2x -3,
不等式的两边都减去2x,由不等式基本性质1,得
3x -2x < 2x-3-2x,
根据不等式基本性质1
即 x < -3.
知识讲解
由(2)可以看出,运用不等式基本性质1 对 3x < 2x-3 进行化简的过程,就是对不等式3x< 2x-3 作了如下变形:
(2) 3x < 2x -3
3x < 2x -3
3x
<
2x
-
3
-
从变形前后的两个不等式可以看出,这种变形就是把不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.
例5 解下列不等式: (1) >50; (2) -4x>3.
为了使不等式>50中不等号的一边变为x,根据
不等式的基本性质2,不等式的两边都除以,不等号
的方向不变,得
x﹥75.
这个不等式的解集在数轴上的表示如图所示:
0
75
解:(1) >50;
知识讲解
为了使不等式-4x﹥3中的不等号的一边变为x,
根据__________________,不等式两边都除以____,
不等号的方向______,得
x﹤- .
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
不等式的基本性质3
-4
改变
(2) -4x>3.
知识讲解
1. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b-10 a -10 .
<
>
x < 2
x < 6
2. 把下列不等式化为x>a或x
(2)2x<x+6.
随 堂 训 练
3.由x<y得到ax<ay,则a应满足条件是( )
A.a≥0 B.a≤0
C.a>0 D.a<0
C
4.已知实数ab若a>b则下列结果正确的是( )
A.a5
D
随堂训练
5.若x>y则下列式子错误的是( )
A.x3>y3
B.3x> 3 y
C.x3>y3
D.>
B
随堂训练
6.利用不等式的性质解下列不等式,并在数轴上表示其解集.
(2)-2x > 3
(1)x-5 > -1
(3)7x < 6x-6
x>4
x<-6
4
0
0
0
-6
x<-
随堂训练
不等式的基本性质
不等式的基本性质2
不等式的基本性质3
→
→
如
那么
如果
那么
应用性质对不等式简单变形
不等式的
基本性质1
如果a>b,那么a+c>b+c,
a-c>b-c
→
课 堂 小 结
