19.2平面直角坐标系(第1课时)教学课件--冀教版数学八年级(下)
文档属性
| 名称 | 19.2平面直角坐标系(第1课时)教学课件--冀教版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 828.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:23:49 | ||
图片预览






文档简介
(共19张PPT)
第 十九章 平面直角坐标系
第十九章 平面直角坐标系
19.2 平面直角坐标系
第1课时 平面直角坐标系
学 习 目 标
1
2
能在给定的直角坐标系中,由点的位置写出它的坐标(难点)
理解平面直角坐标系以及横轴、纵轴、原点、坐标轴等概念。(重点)
温故知新
我们已经学过了数轴,知道数轴上的点与实数一一对应,在建立了数轴之后,我们就可以确定直线上点的位置,如图.
那么,如何确定平面内点的位置呢?
思考:
点A代表的数字为:( )
点B代表的数字为: ( )
﹣1所对应的点是: ( )
5所对应的点是: ( )
﹣4
2
D
C
知识讲解
这就需要引入一个新的工具——平面直角坐标系.
如图是某城市部分街道的示意图.在繁星大道和中山路的交叉口点O处,小亮向交警叔叔问路.
(1)按照交警的指示,小亮能找到图书大厦吗
能
3㎞
知识讲解
(2)如果约定以点O处为参照点,先说出向东(或向西)方向上的距离,再说向北(或向南)方向上的距离,那么图书大厦附近交叉路口P点可以怎样表示
P(东3㎞,北2㎞)
3㎞
知识讲解
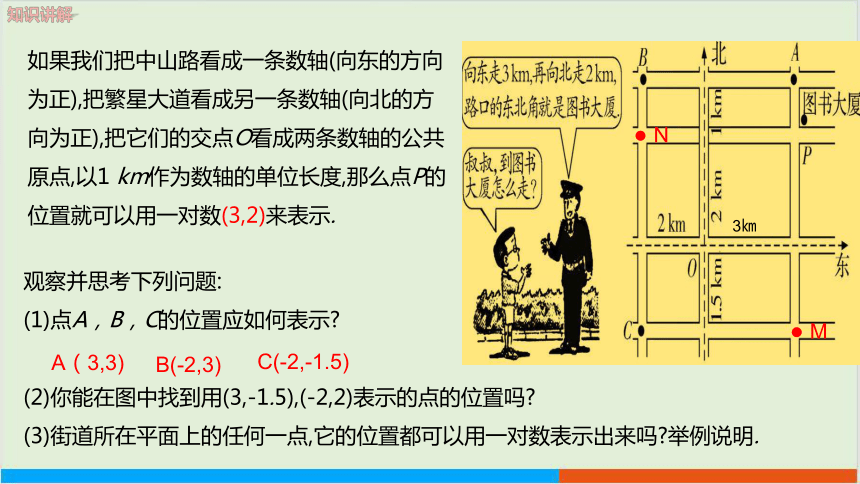
如果我们把中山路看成一条数轴(向东的方向为正),把繁星大道看成另一条数轴(向北的方向为正),把它们的交点O看成两条数轴的公共原点,以1 km作为数轴的单位长度,那么点P的位置就可以用一对数(3,2)来表示.
观察并思考下列问题:
(1)点A,B,C的位置应如何表示
(2)你能在图中找到用(3,-1.5),(-2,2)表示的点的位置吗
(3)街道所在平面上的任何一点,它的位置都可以用一对数表示出来吗 举例说明.
A(3,3)
B(-2,3)
C(-2,-1.5)
3㎞
● M
● N
知识讲解
3
1
4
2
5
-2
-4
-1
-3
y
O
1
2
3
4
5
-4
-3
-2
-1
x
x轴与y轴的公共原点叫坐标原点.
水平方向的数轴叫x轴或横轴;x轴取向右为正方向
竖直方向的数轴叫y轴或纵轴;y轴取向上为正方向
在平面内画两条有公共原点且互相垂直的数轴,构成平面直角坐标系.
思考:已知坐标平面上的一点A,怎样找到一对实数表示它的位置呢?
两条数轴统称为坐标轴
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
点A的横坐标为4
点A的纵坐标为2
有序数对(4, 2)就叫做A的坐标,
横坐标
写在前面
·
B
(-4,1)
知识讲解
思考:已知坐标平面上的一点A,怎样找到一对实数表示它的位置呢?
从点A分别向x轴和y轴做垂线,垂足在x轴和y轴上对应的点表示的实数分别是x和y,我们把有序实数对(x,y)称为点A的坐标。其中,x称为点A的横坐标,y称为点A的纵坐标。点A也记作A(x,y).
记作:A(4,2)
点B的坐标可以记作什么呢?
知识讲解
如图:点A的坐标为(x0,y0)
写出点M,N,P,Q的坐标
点M坐标为(3.5,2)
点N坐标为(﹣4,3)
点P坐标为(﹣3,﹣2)
点Q坐标为(4,﹣2)
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
在平面直角坐标系中找到点A(3,-2)
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
知识讲解
想一想:
知道了点的坐标,如何确定点的位置呢?
例1 如图 在平面直角坐标系中,描出点A(0,4),B(4,2),C(2,-3),D(-2,-3),E(-4,2),并依次连接ABCDEA.
解:在y轴上描出表示4的点,即得A(0,4).
● E
● D
●C
●B
● A
分别过x轴上表示4的点和y轴上表示2的点,作x轴和y轴的垂线,两条垂线的交点就是点B(4,2).
同理,可以描出C,D,E三点.
依次连接ABCDEA,得到图中所示的图形.
知识讲解
实数与数轴上的点具有一一对应关系,由此可知,坐标平面上的点与有序实数对具有一一对应关系,即坐标平面上任意一点都可以用唯一一对有序实数来表示;反过来,任意一对有序实数都可以表示坐标平面上唯一一个点.
总结归纳:
1、如图所示,这是某城市部分简图,每个小正方形的边长为1个单位长度,以火车站所在的位置为坐标原点建立平面直角坐标系,并分别写出各场所的坐标.
解析:以火车站为(0,0),水平方向向右为正,竖直方向向上为正建立平面直角坐标系。
解:如图所示,建立平面直角坐标系,可得:
y
x
o
医院的坐标为(-2,-2),
文化馆的坐标为(-3,1),
体育场的坐标为(-4,3),
宾馆的坐标为(2,2),
市场的坐标为(4,3),
超市的坐标为(2,-3).
课堂训练
2、如图所示,这是某城市部分简图,每个小正方形的边长为1个单位长度,已知火车站的坐标为(1,2),试建立平面直角坐标系,并分别写出其他各地点的坐标.
解析:利用火车站的坐标为(1,2),得出原点位置,进而建立平面直角坐标系得出各点坐标.
解:如图所示,建立平面直角坐标系,可得:
医院的坐标为(-1,0),
文化馆的坐标为(-2,3),
体育场的坐标为(-3,5),
宾馆的坐标为(3,4),
市场的坐标为(5,5),
超市的坐标为(3,-1).
一题多变
3、如图,点A的坐标为( )
A. ( -2,3)
B. ( 2,-3)
C . ( -2,-3)
D . ( 2,3)
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
A
4、如图,点A的坐标为 ,
点B的坐标为 .
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
B
(-2,0)
(0,-2)
5、在直角坐标系中描出下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
平面直角坐标系
平面直角坐标系的概念
在平面直角坐标系中描点
表示平面直角坐标系中点的坐标
课堂小结
第 十九章 平面直角坐标系
第十九章 平面直角坐标系
19.2 平面直角坐标系
第1课时 平面直角坐标系
学 习 目 标
1
2
能在给定的直角坐标系中,由点的位置写出它的坐标(难点)
理解平面直角坐标系以及横轴、纵轴、原点、坐标轴等概念。(重点)
温故知新
我们已经学过了数轴,知道数轴上的点与实数一一对应,在建立了数轴之后,我们就可以确定直线上点的位置,如图.
那么,如何确定平面内点的位置呢?
思考:
点A代表的数字为:( )
点B代表的数字为: ( )
﹣1所对应的点是: ( )
5所对应的点是: ( )
﹣4
2
D
C
知识讲解
这就需要引入一个新的工具——平面直角坐标系.
如图是某城市部分街道的示意图.在繁星大道和中山路的交叉口点O处,小亮向交警叔叔问路.
(1)按照交警的指示,小亮能找到图书大厦吗
能
3㎞
知识讲解
(2)如果约定以点O处为参照点,先说出向东(或向西)方向上的距离,再说向北(或向南)方向上的距离,那么图书大厦附近交叉路口P点可以怎样表示
P(东3㎞,北2㎞)
3㎞
知识讲解
如果我们把中山路看成一条数轴(向东的方向为正),把繁星大道看成另一条数轴(向北的方向为正),把它们的交点O看成两条数轴的公共原点,以1 km作为数轴的单位长度,那么点P的位置就可以用一对数(3,2)来表示.
观察并思考下列问题:
(1)点A,B,C的位置应如何表示
(2)你能在图中找到用(3,-1.5),(-2,2)表示的点的位置吗
(3)街道所在平面上的任何一点,它的位置都可以用一对数表示出来吗 举例说明.
A(3,3)
B(-2,3)
C(-2,-1.5)
3㎞
● M
● N
知识讲解
3
1
4
2
5
-2
-4
-1
-3
y
O
1
2
3
4
5
-4
-3
-2
-1
x
x轴与y轴的公共原点叫坐标原点.
水平方向的数轴叫x轴或横轴;x轴取向右为正方向
竖直方向的数轴叫y轴或纵轴;y轴取向上为正方向
在平面内画两条有公共原点且互相垂直的数轴,构成平面直角坐标系.
思考:已知坐标平面上的一点A,怎样找到一对实数表示它的位置呢?
两条数轴统称为坐标轴
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
点A的横坐标为4
点A的纵坐标为2
有序数对(4, 2)就叫做A的坐标,
横坐标
写在前面
·
B
(-4,1)
知识讲解
思考:已知坐标平面上的一点A,怎样找到一对实数表示它的位置呢?
从点A分别向x轴和y轴做垂线,垂足在x轴和y轴上对应的点表示的实数分别是x和y,我们把有序实数对(x,y)称为点A的坐标。其中,x称为点A的横坐标,y称为点A的纵坐标。点A也记作A(x,y).
记作:A(4,2)
点B的坐标可以记作什么呢?
知识讲解
如图:点A的坐标为(x0,y0)
写出点M,N,P,Q的坐标
点M坐标为(3.5,2)
点N坐标为(﹣4,3)
点P坐标为(﹣3,﹣2)
点Q坐标为(4,﹣2)
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
在平面直角坐标系中找到点A(3,-2)
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
知识讲解
想一想:
知道了点的坐标,如何确定点的位置呢?
例1 如图 在平面直角坐标系中,描出点A(0,4),B(4,2),C(2,-3),D(-2,-3),E(-4,2),并依次连接ABCDEA.
解:在y轴上描出表示4的点,即得A(0,4).
● E
● D
●C
●B
● A
分别过x轴上表示4的点和y轴上表示2的点,作x轴和y轴的垂线,两条垂线的交点就是点B(4,2).
同理,可以描出C,D,E三点.
依次连接ABCDEA,得到图中所示的图形.
知识讲解
实数与数轴上的点具有一一对应关系,由此可知,坐标平面上的点与有序实数对具有一一对应关系,即坐标平面上任意一点都可以用唯一一对有序实数来表示;反过来,任意一对有序实数都可以表示坐标平面上唯一一个点.
总结归纳:
1、如图所示,这是某城市部分简图,每个小正方形的边长为1个单位长度,以火车站所在的位置为坐标原点建立平面直角坐标系,并分别写出各场所的坐标.
解析:以火车站为(0,0),水平方向向右为正,竖直方向向上为正建立平面直角坐标系。
解:如图所示,建立平面直角坐标系,可得:
y
x
o
医院的坐标为(-2,-2),
文化馆的坐标为(-3,1),
体育场的坐标为(-4,3),
宾馆的坐标为(2,2),
市场的坐标为(4,3),
超市的坐标为(2,-3).
课堂训练
2、如图所示,这是某城市部分简图,每个小正方形的边长为1个单位长度,已知火车站的坐标为(1,2),试建立平面直角坐标系,并分别写出其他各地点的坐标.
解析:利用火车站的坐标为(1,2),得出原点位置,进而建立平面直角坐标系得出各点坐标.
解:如图所示,建立平面直角坐标系,可得:
医院的坐标为(-1,0),
文化馆的坐标为(-2,3),
体育场的坐标为(-3,5),
宾馆的坐标为(3,4),
市场的坐标为(5,5),
超市的坐标为(3,-1).
一题多变
3、如图,点A的坐标为( )
A. ( -2,3)
B. ( 2,-3)
C . ( -2,-3)
D . ( 2,3)
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
A
4、如图,点A的坐标为 ,
点B的坐标为 .
x
y
O
1
2
3
-3
-2
-1
1
2
-1
-2
A
B
(-2,0)
(0,-2)
5、在直角坐标系中描出下列各点:
A(4,3),
B(-2,3),
C(-4,-1),
D(2,-2).
3
1
4
2
5
-2
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
B
·
A
·
D
·
C
平面直角坐标系
平面直角坐标系的概念
在平面直角坐标系中描点
表示平面直角坐标系中点的坐标
课堂小结
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
