19.2平面直角坐标系(第2课时)教学课件--冀教版数学八年级(下)
文档属性
| 名称 | 19.2平面直角坐标系(第2课时)教学课件--冀教版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 551.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:23:49 | ||
图片预览




文档简介
(共21张PPT)
第 十九章 平面直角坐标系
第十九章 平面直角坐标系
19.2 平面直角坐标系
第2课时 平面坐标系中点的坐标特征
学 习 目 标
1
2
掌握点关于坐标轴及原点的对称点的坐标特征.(难点)
掌握平面直角坐标系中各象限、坐标轴上点的坐标特征.(重点)
温故知新
3
1
4
2
5
-2
-4
-1
-3
y
O
1
2
3
4
5
-4
-3
-2
-1
x
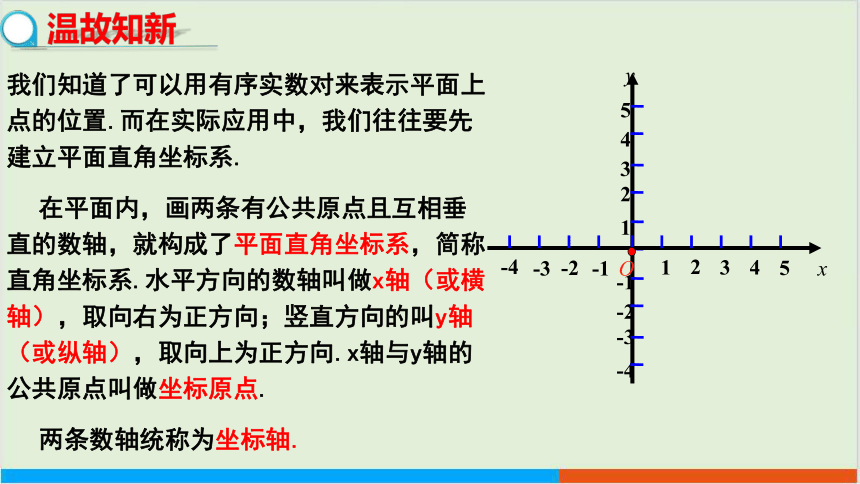
我们知道了可以用有序实数对来表示平面上点的位置.而在实际应用中,我们往往要先建立平面直角坐标系.
在平面内,画两条有公共原点且互相垂直的数轴,就构成了平面直角坐标系,简称直角坐标系.水平方向的数轴叫做x轴(或横轴),取向右为正方向;竖直方向的叫y轴(或纵轴),取向上为正方向.x轴与y轴的公共原点叫做坐标原点.
两条数轴统称为坐标轴.
y
54321
- 5 -4 -3 -2 -1 0 1 2 3 4 5 x
认
识
象
限
-1
-2
-3
-4
-5
第一象限
第二象限
第三象限
第四象限
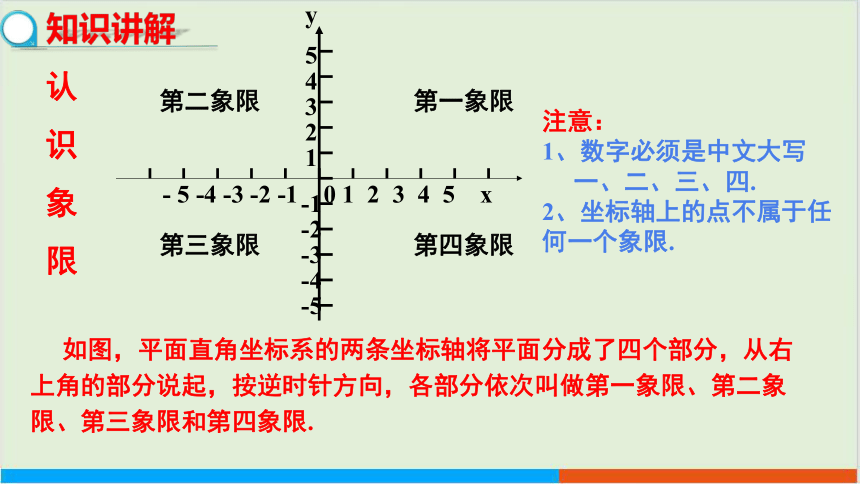
如图,平面直角坐标系的两条坐标轴将平面分成了四个部分,从右上角的部分说起,按逆时针方向,各部分依次叫做第一象限、第二象限、第三象限和第四象限.
知识讲解
注意:
1、数字必须是中文大写
一、二、三、四.
2、坐标轴上的点不属于任何一个象限.
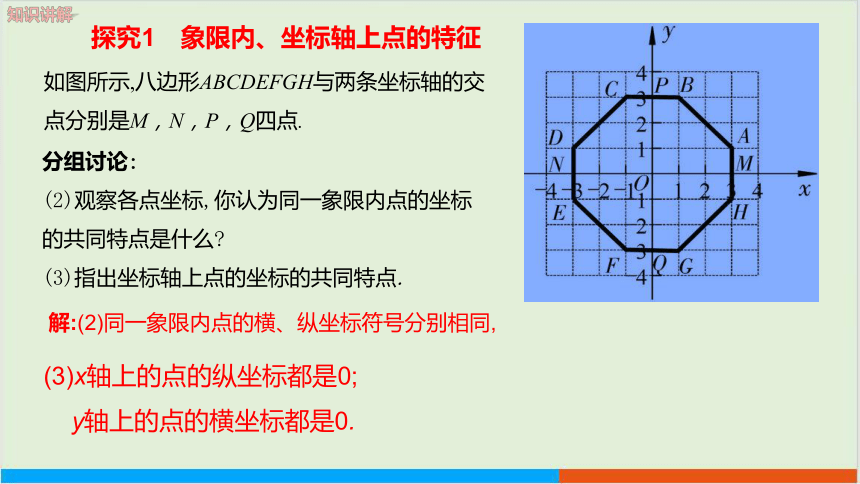
探究1 象限内、坐标轴上点的特征
如图所示,八边形ABCDEFGH与两条坐标轴的交点分别是M,N,P,Q四点.
分组讨论:
(1)分别写出图中各点的坐标.
A(3,1)
B(1,3)
C(-1,3)
F(-1,-3),
D(-3,1),
E(-3,-1),
G(1,-3),
N(-3,0).
M(3,0)
H(3,-1),
P(0,3)
Q(0,-3),
解:
探究1 象限内、坐标轴上点的特征
如图所示,八边形ABCDEFGH与两条坐标轴的交点分别是M,N,P,Q四点.
分组讨论:
(2)观察各点坐标,你认为同一象限内点的坐标的共同特点是什么
(3)指出坐标轴上点的坐标的共同特点.
解:(2)同一象限内点的横、纵坐标符号分别相同,
(3)x轴上的点的纵坐标都是0;
y轴上的点的横坐标都是0.
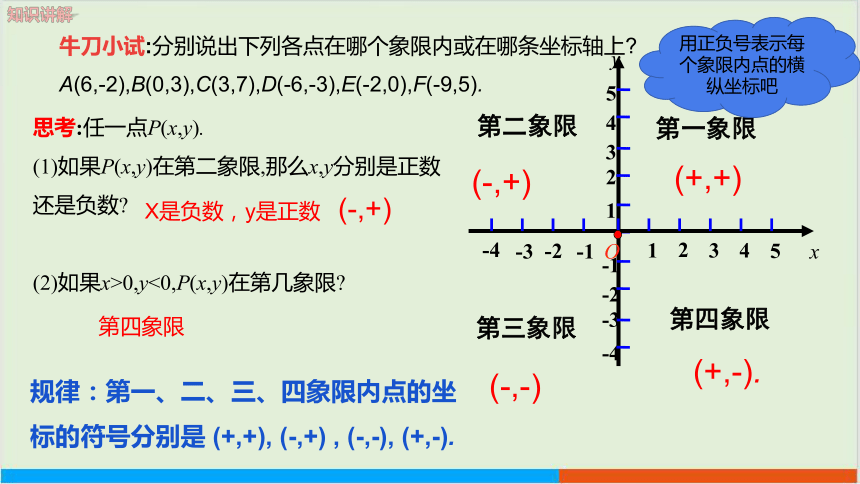
牛刀小试:分别说出下列各点在哪个象限内或在哪条坐标轴上
A(6,-2),B(0,3),C(3,7),D(-6,-3),E(-2,0),F(-9,5).
思考:任一点P(x,y).
(1)如果P(x,y)在第二象限,那么x,y分别是正数还是负数
(2)如果x>0,y<0,P(x,y)在第几象限
3
1
4
2
5
-2
-4
-1
-3
y
O
1
2
3
4
5
-4
-3
-2
-1
x
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-).
规律:第一、二、三、四象限内点的坐标的符号分别是 (+,+), (-,+) , (-,-), (+,-).
X是负数,y是正数 (-,+)
第四象限
用正负号表示每个象限内点的横纵坐标吧
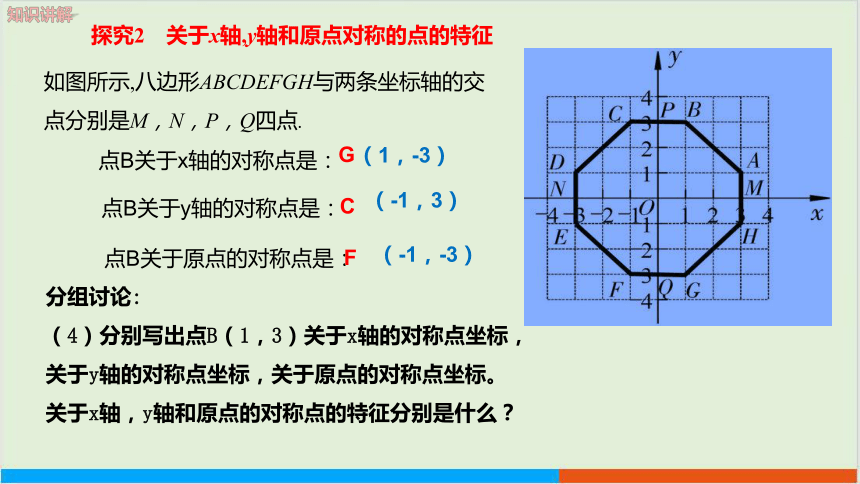
探究2 关于x轴,y轴和原点对称的点的特征
如图所示,八边形ABCDEFGH与两条坐标轴的交点分别是M,N,P,Q四点.
分组讨论:
(4)分别写出点B(1,3)关于x轴的对称点坐标,关于y轴的对称点坐标,关于原点的对称点坐标。关于x轴,y轴和原点的对称点的特征分别是什么?
点B关于x轴的对称点是:
点B关于y轴的对称点是:
点B关于原点的对称点是:
G
C
F
(1,-3)
(-1,3)
(-1,-3)
共同归纳:
(1)关于x轴对称的两点
(2)关于y轴对称的两点
(3)关于原点对称的两点
横坐标相同,纵坐标互为相反数;
横坐标互为相反数,纵坐标相同;
横、纵坐标都互为相反数.
例2 建立直角坐标系,并解决下列问题.
(1)描出下列各点,并把各点依次连接成封闭图形.
A(1,-1),B(3,-1),C(3,1),D(1,1),E(1,3),F(-1,3),G(-1,1),H(-3,1),
I(-3,-1),J(-1,-1),K(-1,-3),L(1,-3).
(2)观察所得的图形,它是轴对称图形吗 如果是轴对称图形,画出它的对称轴.
(3)在画出的图形中,分别写出关于x轴,y轴和原点的对称点.
解:(1)描点,连线后得到的图形如图所示.
(2)这个图形是轴对称图形,它有四条对称轴:x轴,y轴,l1,l2.
(3)关于x轴的对称点分别是点A和点D,点B和点C,点E和点L,点F和点K,点G和点J,点H和点I.关于y轴的对称点分别是点A和点J,点B和点I,点C和点H,点D和点G,点E和点F,点L和点K.关于原点的对称点分别是点A和点G,点B和点H,点C和点I,点D和点J,点E和点K,点F和点L.
总结一下:平面直角坐标系中相关点的坐标的特征.
(1)在平面直角坐标系中,x轴和y轴将平面分成四个部分,按逆时针方向依次叫做第一象限、第二象限、第三象限、第四象限.坐标轴上的点不属于任何一个象限.
(2)各象限内点的坐标有以下特征:如果点A(x,y)在第一象限,那么x>0,y>0;如果点A(x,y)在第二象限,那么x<0,y>0;如果点A(x,y)在第三象限,那么x<0,y<0;如果点A(x,y)在第四象限,那么x>0,y<0.
(3)如果点A(x,y)在x轴上,那么y=0,x为任意实数;如果点A(x,y)在y轴上,那么x=0,y为任意实数;如果点A(x,y)既在x轴上又在y轴上,那么x=0且y=0.
(4)平面直角坐标系中的点P(x,y),关于x轴对称点的坐标为(x,-y),关于y轴对称点的坐标为(-x,y),关于原点对称点的坐标为(-x,-y).
O
1
1
-2
x
y
点M(-3,4)到x轴、y轴和坐标原点的距离分别多少?
M(-3,4)
N
H
相互交流,共同探讨:
MN=4
MH=3
MO=5
﹣1
2
2
﹣1
-2
①点P(a,b)到x轴的距离是
②点P(a,b)到y轴的距离是
③点P(a,b)与坐标原点的距离是
x
y
o
P(a,b)
M
N
纵坐标的绝对值
横坐标的绝对值
总结规律
1.在平面直角坐标系中,点(1,5)所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
2.已知点P(0,a)在y轴的负半轴上,则点Q(-a2-1,-a+1)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
3.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
课堂训练
4.建立直角坐标系,解决以下问题:
(1)画出下列各点,并把各点依次连接成封闭图形.
A(-2,3),B(2,3),C(5,0),D(2,-3),
E(-2,-3),F(-5,0).
(2)指出上面各点所在的象限或坐标轴
(3)分别写出上面各点关于x轴,y轴和原点的对称点.
y
x
A(-2,3)
B(2,3)
C(0,5)
D(2,-3)
E(-2,-3)
F(-5,0)
(1)画出的点及图形如图所示:
(2)由图可知:点A在第二象限内、点B在第一象限内、点D在第四象限内、点E在第三象限内,F、C两点均位于X轴上。
(3)C,F关于y轴及原点对称;
A与B,E与D分别关于y轴对称;
A与E,B与D关于x轴对称;
A与D,B与E关于原点对称.
5.如图所示,点A(-2,1)到y轴的距离为 ( )
A.-2 B.1 C.2 D.
C
6.如图所示,下列各点在阴影区域内的是 ( )
A.(3,2) B.(-3,2)
C.(3,-2) D.(-3,-2)
A
7.若点P(2k-1,1-k)在第四象限,则k的取值范围为 ( )
A.k>1 B.k<
C.k> D.A
8.点P(m+3,m-1)在x轴上,则点P的坐标为 ( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
C
点的位置与点的坐标的关系
象限的概念
关于x轴、y轴、原点对称点的坐标的特点
点的位置与坐标的关系
课堂小结
第 十九章 平面直角坐标系
第十九章 平面直角坐标系
19.2 平面直角坐标系
第2课时 平面坐标系中点的坐标特征
学 习 目 标
1
2
掌握点关于坐标轴及原点的对称点的坐标特征.(难点)
掌握平面直角坐标系中各象限、坐标轴上点的坐标特征.(重点)
温故知新
3
1
4
2
5
-2
-4
-1
-3
y
O
1
2
3
4
5
-4
-3
-2
-1
x
我们知道了可以用有序实数对来表示平面上点的位置.而在实际应用中,我们往往要先建立平面直角坐标系.
在平面内,画两条有公共原点且互相垂直的数轴,就构成了平面直角坐标系,简称直角坐标系.水平方向的数轴叫做x轴(或横轴),取向右为正方向;竖直方向的叫y轴(或纵轴),取向上为正方向.x轴与y轴的公共原点叫做坐标原点.
两条数轴统称为坐标轴.
y
54321
- 5 -4 -3 -2 -1 0 1 2 3 4 5 x
认
识
象
限
-1
-2
-3
-4
-5
第一象限
第二象限
第三象限
第四象限
如图,平面直角坐标系的两条坐标轴将平面分成了四个部分,从右上角的部分说起,按逆时针方向,各部分依次叫做第一象限、第二象限、第三象限和第四象限.
知识讲解
注意:
1、数字必须是中文大写
一、二、三、四.
2、坐标轴上的点不属于任何一个象限.
探究1 象限内、坐标轴上点的特征
如图所示,八边形ABCDEFGH与两条坐标轴的交点分别是M,N,P,Q四点.
分组讨论:
(1)分别写出图中各点的坐标.
A(3,1)
B(1,3)
C(-1,3)
F(-1,-3),
D(-3,1),
E(-3,-1),
G(1,-3),
N(-3,0).
M(3,0)
H(3,-1),
P(0,3)
Q(0,-3),
解:
探究1 象限内、坐标轴上点的特征
如图所示,八边形ABCDEFGH与两条坐标轴的交点分别是M,N,P,Q四点.
分组讨论:
(2)观察各点坐标,你认为同一象限内点的坐标的共同特点是什么
(3)指出坐标轴上点的坐标的共同特点.
解:(2)同一象限内点的横、纵坐标符号分别相同,
(3)x轴上的点的纵坐标都是0;
y轴上的点的横坐标都是0.
牛刀小试:分别说出下列各点在哪个象限内或在哪条坐标轴上
A(6,-2),B(0,3),C(3,7),D(-6,-3),E(-2,0),F(-9,5).
思考:任一点P(x,y).
(1)如果P(x,y)在第二象限,那么x,y分别是正数还是负数
(2)如果x>0,y<0,P(x,y)在第几象限
3
1
4
2
5
-2
-4
-1
-3
y
O
1
2
3
4
5
-4
-3
-2
-1
x
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-).
规律:第一、二、三、四象限内点的坐标的符号分别是 (+,+), (-,+) , (-,-), (+,-).
X是负数,y是正数 (-,+)
第四象限
用正负号表示每个象限内点的横纵坐标吧
探究2 关于x轴,y轴和原点对称的点的特征
如图所示,八边形ABCDEFGH与两条坐标轴的交点分别是M,N,P,Q四点.
分组讨论:
(4)分别写出点B(1,3)关于x轴的对称点坐标,关于y轴的对称点坐标,关于原点的对称点坐标。关于x轴,y轴和原点的对称点的特征分别是什么?
点B关于x轴的对称点是:
点B关于y轴的对称点是:
点B关于原点的对称点是:
G
C
F
(1,-3)
(-1,3)
(-1,-3)
共同归纳:
(1)关于x轴对称的两点
(2)关于y轴对称的两点
(3)关于原点对称的两点
横坐标相同,纵坐标互为相反数;
横坐标互为相反数,纵坐标相同;
横、纵坐标都互为相反数.
例2 建立直角坐标系,并解决下列问题.
(1)描出下列各点,并把各点依次连接成封闭图形.
A(1,-1),B(3,-1),C(3,1),D(1,1),E(1,3),F(-1,3),G(-1,1),H(-3,1),
I(-3,-1),J(-1,-1),K(-1,-3),L(1,-3).
(2)观察所得的图形,它是轴对称图形吗 如果是轴对称图形,画出它的对称轴.
(3)在画出的图形中,分别写出关于x轴,y轴和原点的对称点.
解:(1)描点,连线后得到的图形如图所示.
(2)这个图形是轴对称图形,它有四条对称轴:x轴,y轴,l1,l2.
(3)关于x轴的对称点分别是点A和点D,点B和点C,点E和点L,点F和点K,点G和点J,点H和点I.关于y轴的对称点分别是点A和点J,点B和点I,点C和点H,点D和点G,点E和点F,点L和点K.关于原点的对称点分别是点A和点G,点B和点H,点C和点I,点D和点J,点E和点K,点F和点L.
总结一下:平面直角坐标系中相关点的坐标的特征.
(1)在平面直角坐标系中,x轴和y轴将平面分成四个部分,按逆时针方向依次叫做第一象限、第二象限、第三象限、第四象限.坐标轴上的点不属于任何一个象限.
(2)各象限内点的坐标有以下特征:如果点A(x,y)在第一象限,那么x>0,y>0;如果点A(x,y)在第二象限,那么x<0,y>0;如果点A(x,y)在第三象限,那么x<0,y<0;如果点A(x,y)在第四象限,那么x>0,y<0.
(3)如果点A(x,y)在x轴上,那么y=0,x为任意实数;如果点A(x,y)在y轴上,那么x=0,y为任意实数;如果点A(x,y)既在x轴上又在y轴上,那么x=0且y=0.
(4)平面直角坐标系中的点P(x,y),关于x轴对称点的坐标为(x,-y),关于y轴对称点的坐标为(-x,y),关于原点对称点的坐标为(-x,-y).
O
1
1
-2
x
y
点M(-3,4)到x轴、y轴和坐标原点的距离分别多少?
M(-3,4)
N
H
相互交流,共同探讨:
MN=4
MH=3
MO=5
﹣1
2
2
﹣1
-2
①点P(a,b)到x轴的距离是
②点P(a,b)到y轴的距离是
③点P(a,b)与坐标原点的距离是
x
y
o
P(a,b)
M
N
纵坐标的绝对值
横坐标的绝对值
总结规律
1.在平面直角坐标系中,点(1,5)所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
2.已知点P(0,a)在y轴的负半轴上,则点Q(-a2-1,-a+1)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
3.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
课堂训练
4.建立直角坐标系,解决以下问题:
(1)画出下列各点,并把各点依次连接成封闭图形.
A(-2,3),B(2,3),C(5,0),D(2,-3),
E(-2,-3),F(-5,0).
(2)指出上面各点所在的象限或坐标轴
(3)分别写出上面各点关于x轴,y轴和原点的对称点.
y
x
A(-2,3)
B(2,3)
C(0,5)
D(2,-3)
E(-2,-3)
F(-5,0)
(1)画出的点及图形如图所示:
(2)由图可知:点A在第二象限内、点B在第一象限内、点D在第四象限内、点E在第三象限内,F、C两点均位于X轴上。
(3)C,F关于y轴及原点对称;
A与B,E与D分别关于y轴对称;
A与E,B与D关于x轴对称;
A与D,B与E关于原点对称.
5.如图所示,点A(-2,1)到y轴的距离为 ( )
A.-2 B.1 C.2 D.
C
6.如图所示,下列各点在阴影区域内的是 ( )
A.(3,2) B.(-3,2)
C.(3,-2) D.(-3,-2)
A
7.若点P(2k-1,1-k)在第四象限,则k的取值范围为 ( )
A.k>1 B.k<
C.k> D.
8.点P(m+3,m-1)在x轴上,则点P的坐标为 ( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
C
点的位置与点的坐标的关系
象限的概念
关于x轴、y轴、原点对称点的坐标的特点
点的位置与坐标的关系
课堂小结
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
