20.3函数的表示 教学课件--冀教版数学八年级(下)
文档属性
| 名称 | 20.3函数的表示 教学课件--冀教版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
第 二十章 函数
第二十章 函数
20.3 函数的表示
学 习 目 标
1
2
了解函数各种表示方法的特点,能选择适当的方法表示实际问题中的函数关系,发展符号感;(重点)
学会画函数的图像,初步体会数形结合的思想方法。 (难点)
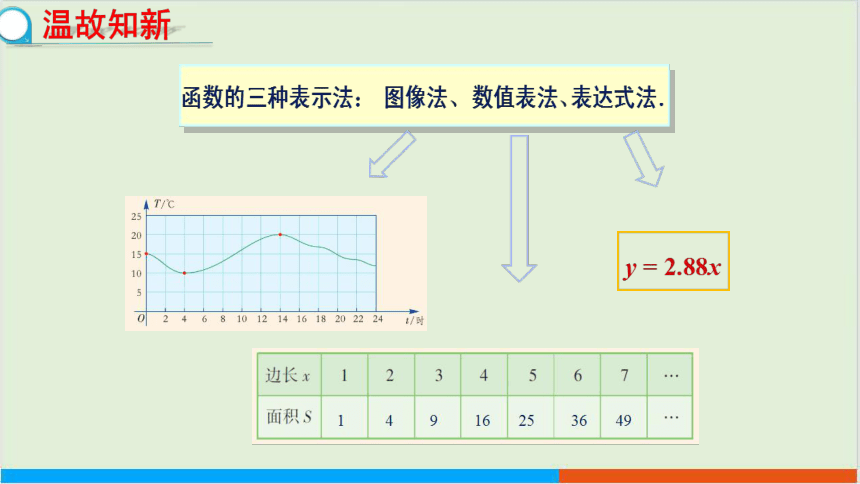
温故知新
新课导入
人们发现,声音在空气中传播的速度(简称声速)随气温的变化而变化.某研究者通过实验得到了这样一些关于气温x与声速y对应的数据:
实际上,这就是用数值表来表达关于声速y与气温x之间的函数关系.
问题: 1.你还能用其他方法表示声速y与气温x之间的函数关系吗
2.这些表示方法有什么特点
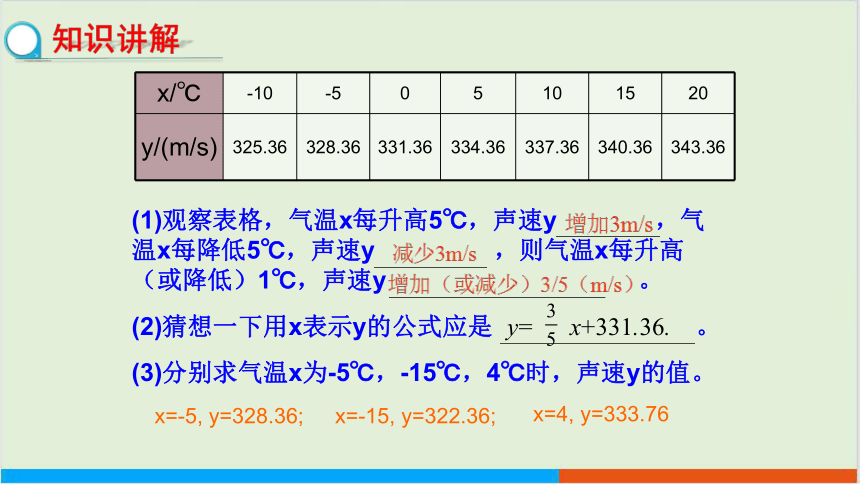
(2)猜想一下用x表示y的公式应是 。
(1)观察表格,气温x每升高5℃,声速y ,气温x每降低5℃,声速y ,则气温x每升高(或降低)1℃,声速y 。
(3)分别求气温x为-5℃,-15℃,4℃时,声速y的值。
x=-5, y=328.36;
x/℃ -10 -5 0 5 10 15 20
y/(m/s) 325.36 328.36 331.36 334.36 337.36 340.36 343.36
x=-15, y=322.36;
x=4, y=333.76
知识讲解
y= x+331.36.
知识讲解
(4)用表达式表示函数的特点是什么?
这个表达式更加全面、准确地反映了声速y(m/s)和气温x(℃)之间的对应关系.利用它,可以方便地得到与x(℃)值对应的y(m/s)的值.
如:当气温x为-4(℃)时,声速y为 ×(-4)+331.36=328.96(m/s),当气温x为28(℃)时,声速y为 ×28+331.36=348.16(m/s)……
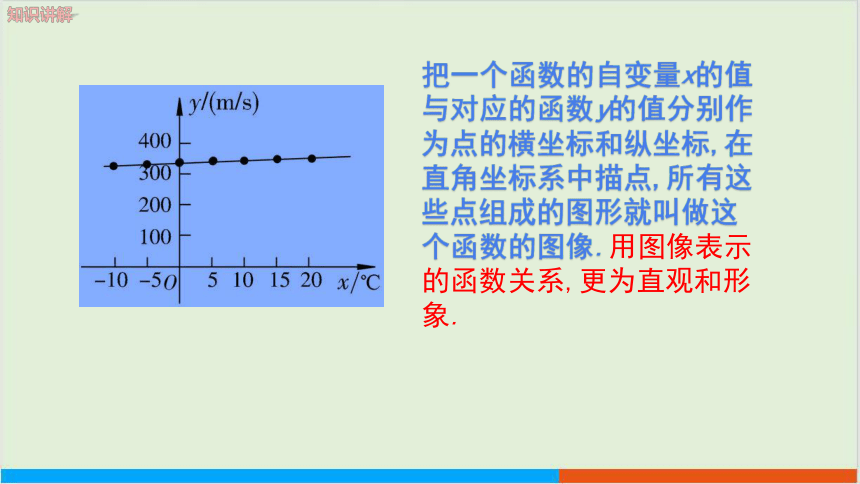
声速y(m/s)与气温x(℃)之间的函数关系,还可以借助图形表示出来,具体可以这样做:
1.画出直角坐标系,用横轴上的点表示气温x(℃),用纵轴上的点表示声速y(m/s).
2.借助于表格(或表达式),找出x和y的若干对对应值,
如(-5,328.36),(0,331.36),(5,334.36),(10,337.36),(15,340.36),….分别以每对值为横、纵坐标,确定出坐标系中相应的点.
3.用平滑的线将这些点连起来,就得到声速y(m/s)和气温x(℃)之间用图形表示的函数关系,如图所示.
把一个函数的自变量x的值与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系中描点,所有这些点组成的图形就叫做这个函数的图像.用图像表示的函数关系,更为直观和形象.
[知识拓展]
一般来说,函数图像是由直角坐标系中的一系列点组成的.图像上每一点的坐标(x,y)代表了函数中变量的一对对应值,它的横坐标表示自变量的某一个值,纵坐标表示与它相对应的函数值.
(1)通常情况下,横坐标表示自变量,纵坐标表示函数值;
(2)函数图像代表了函数的几何意义,体现了数形结合的思想;
(3)图像上每一个点的坐标都满足函数关系式,满足函数关系式的任意一对x,y的值所对应的点都在函数图像上.
x/℃ -10 -5 0 5 10 15 20
y/(m/s) 325.36 328.36 331.36 334.36 337.36 340.36 343.36
x … -2 -1 0 1 2 …
y … -3 -1 1 3 5 …
例:在直角坐标系中,画出函数y=2x+1的图像.
用计算器可以求出任何一个非负数的算术平方根,显示器显示的结果随输入数的变化而变化.设输入的数为x,显示的结果为y,程序如图所示.
(1)请写出y与x之间的函数关系式,并指出自变量的取值范围.
(3)借助这些对应的数值画出这个函数的图像.
做一做
(2)根据函数关系式,填写表格
(y= (x≥0).)
:
x 0 1 4 9 16
y
0
1
3
4
2
课堂训练
1.下图是护士统计一位甲型H1N1流感疑似病人的体温变化图,这位病人在16时的体温约是 ( )
A.37.8 ℃ B.38 ℃ C.38.7 ℃ D.39.1 ℃
C
2.小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图像是 ( )
B
3.下图表示某地的气温变化情况.
(1)在 时气温最高,为 ;
(2)在 时到 时这段时间气温是逐渐上升的.
14
15 ℃
8
14
600
12
200
4.河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图像如图所示,则水泵抽水前,河道内有 米3的水,水泵最多抽 小时,水泵抽8小时后,河道剩水量是 米3.
5.大年三十晚上,小六驾车从家出发到烟花燃放指定点去燃放烟花爆竹,小六驾车匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后小六加快速度继续匀速行驶,零点之前到达指定燃放地点,燃放结束后,小六驾车匀速返回.其中,x表示小六从家出发后所用时间,y表示小六离家的距离.下图中能反映y与x的函数关系的大致图像是 ( )
A
6.一家电信公司提供两种手机的月通话收费方式供用户选择,其中一种有月租费,另一种无月租费.这两种收费方式的通话费用y(元)与通话时间x(分钟)之间的函数关系如图所示.小红根据图像得出下列结论:
①l1描述的是无月租费的收费方式;
②l2描述的是有月租费的收费方式;
③当每月的通话时间为500分钟时,选择有
月租费的收费方式省钱.
其中正确结论的个数是 ( )
A.0 B.1 C.2 D.3
D
7.某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是 ( )
A.小强从家到公共汽车站步行了2公里
B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时
D.小强乘公共汽车用了20分钟
D
函
数
的
表
示
数值表
图 像
表达式
数据
具体
简单
明了
形象
直观
画函数图像步骤
列点描点
连线
课堂小结
第 二十章 函数
第二十章 函数
20.3 函数的表示
学 习 目 标
1
2
了解函数各种表示方法的特点,能选择适当的方法表示实际问题中的函数关系,发展符号感;(重点)
学会画函数的图像,初步体会数形结合的思想方法。 (难点)
温故知新
新课导入
人们发现,声音在空气中传播的速度(简称声速)随气温的变化而变化.某研究者通过实验得到了这样一些关于气温x与声速y对应的数据:
实际上,这就是用数值表来表达关于声速y与气温x之间的函数关系.
问题: 1.你还能用其他方法表示声速y与气温x之间的函数关系吗
2.这些表示方法有什么特点
(2)猜想一下用x表示y的公式应是 。
(1)观察表格,气温x每升高5℃,声速y ,气温x每降低5℃,声速y ,则气温x每升高(或降低)1℃,声速y 。
(3)分别求气温x为-5℃,-15℃,4℃时,声速y的值。
x=-5, y=328.36;
x/℃ -10 -5 0 5 10 15 20
y/(m/s) 325.36 328.36 331.36 334.36 337.36 340.36 343.36
x=-15, y=322.36;
x=4, y=333.76
知识讲解
y= x+331.36.
知识讲解
(4)用表达式表示函数的特点是什么?
这个表达式更加全面、准确地反映了声速y(m/s)和气温x(℃)之间的对应关系.利用它,可以方便地得到与x(℃)值对应的y(m/s)的值.
如:当气温x为-4(℃)时,声速y为 ×(-4)+331.36=328.96(m/s),当气温x为28(℃)时,声速y为 ×28+331.36=348.16(m/s)……
声速y(m/s)与气温x(℃)之间的函数关系,还可以借助图形表示出来,具体可以这样做:
1.画出直角坐标系,用横轴上的点表示气温x(℃),用纵轴上的点表示声速y(m/s).
2.借助于表格(或表达式),找出x和y的若干对对应值,
如(-5,328.36),(0,331.36),(5,334.36),(10,337.36),(15,340.36),….分别以每对值为横、纵坐标,确定出坐标系中相应的点.
3.用平滑的线将这些点连起来,就得到声速y(m/s)和气温x(℃)之间用图形表示的函数关系,如图所示.
把一个函数的自变量x的值与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系中描点,所有这些点组成的图形就叫做这个函数的图像.用图像表示的函数关系,更为直观和形象.
[知识拓展]
一般来说,函数图像是由直角坐标系中的一系列点组成的.图像上每一点的坐标(x,y)代表了函数中变量的一对对应值,它的横坐标表示自变量的某一个值,纵坐标表示与它相对应的函数值.
(1)通常情况下,横坐标表示自变量,纵坐标表示函数值;
(2)函数图像代表了函数的几何意义,体现了数形结合的思想;
(3)图像上每一个点的坐标都满足函数关系式,满足函数关系式的任意一对x,y的值所对应的点都在函数图像上.
x/℃ -10 -5 0 5 10 15 20
y/(m/s) 325.36 328.36 331.36 334.36 337.36 340.36 343.36
x … -2 -1 0 1 2 …
y … -3 -1 1 3 5 …
例:在直角坐标系中,画出函数y=2x+1的图像.
用计算器可以求出任何一个非负数的算术平方根,显示器显示的结果随输入数的变化而变化.设输入的数为x,显示的结果为y,程序如图所示.
(1)请写出y与x之间的函数关系式,并指出自变量的取值范围.
(3)借助这些对应的数值画出这个函数的图像.
做一做
(2)根据函数关系式,填写表格
(y= (x≥0).)
:
x 0 1 4 9 16
y
0
1
3
4
2
课堂训练
1.下图是护士统计一位甲型H1N1流感疑似病人的体温变化图,这位病人在16时的体温约是 ( )
A.37.8 ℃ B.38 ℃ C.38.7 ℃ D.39.1 ℃
C
2.小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图像是 ( )
B
3.下图表示某地的气温变化情况.
(1)在 时气温最高,为 ;
(2)在 时到 时这段时间气温是逐渐上升的.
14
15 ℃
8
14
600
12
200
4.河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图像如图所示,则水泵抽水前,河道内有 米3的水,水泵最多抽 小时,水泵抽8小时后,河道剩水量是 米3.
5.大年三十晚上,小六驾车从家出发到烟花燃放指定点去燃放烟花爆竹,小六驾车匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后小六加快速度继续匀速行驶,零点之前到达指定燃放地点,燃放结束后,小六驾车匀速返回.其中,x表示小六从家出发后所用时间,y表示小六离家的距离.下图中能反映y与x的函数关系的大致图像是 ( )
A
6.一家电信公司提供两种手机的月通话收费方式供用户选择,其中一种有月租费,另一种无月租费.这两种收费方式的通话费用y(元)与通话时间x(分钟)之间的函数关系如图所示.小红根据图像得出下列结论:
①l1描述的是无月租费的收费方式;
②l2描述的是有月租费的收费方式;
③当每月的通话时间为500分钟时,选择有
月租费的收费方式省钱.
其中正确结论的个数是 ( )
A.0 B.1 C.2 D.3
D
7.某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是 ( )
A.小强从家到公共汽车站步行了2公里
B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时
D.小强乘公共汽车用了20分钟
D
函
数
的
表
示
数值表
图 像
表达式
数据
具体
简单
明了
形象
直观
画函数图像步骤
列点描点
连线
课堂小结
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
