第9章多边形9.2多边形的内角和与外角和(第1课时) 教案--华师大版初中数学七年级下
文档属性
| 名称 | 第9章多边形9.2多边形的内角和与外角和(第1课时) 教案--华师大版初中数学七年级下 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览

文档简介
第9章 多边形
9.2 多边形的内角和与外角和
第1课时 多边形的内角和
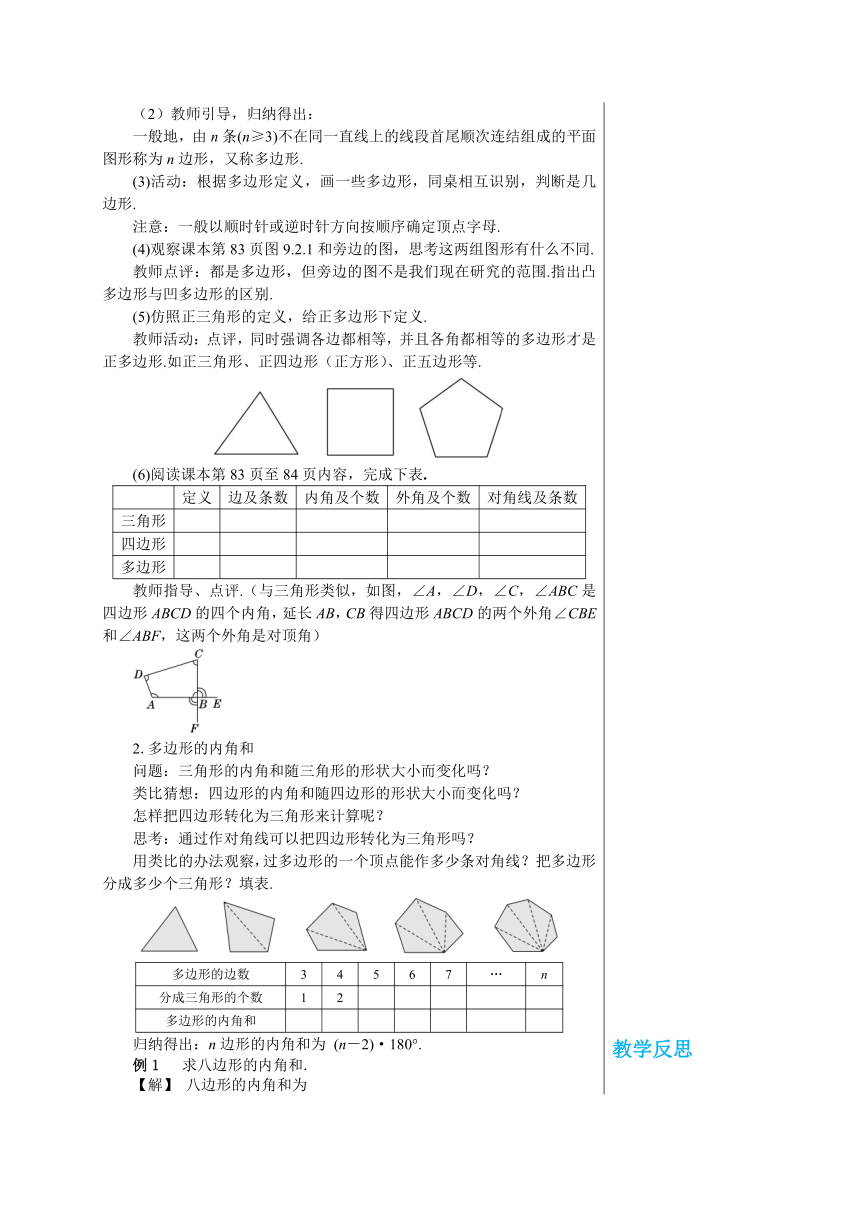
教学目标 1.使学生了解多边形、正多边形及多边形的内角、外角、对角线等概念. 2.使学生通过不同方法探索多边形的内角和公式,并会利用它们进行有关计算. 3.通过把多边形转化为三角形,体会转化思想在几何中的运用,让学生体会从特殊到一般的认识问题的方法. 教学重难点 重点: 探索多边形的内角和公式,应用多边形内角和解决有关的问题. 难点:多边形的内角和公式的推导. 教学过程 导入新课 某小区健身广场中心的边缘是一个五边形(如图),你能求出它的五个内角的和吗? 探究新知 合作探究 1.多边形的有关概念 (1)我们已经知道三角形的定义,那么能否模仿三角形的定义来给四边形、五边形下定义? 教师活动:鼓励、点评. 如图1是由不在同一直线上的4条线段首尾顺次连结组成的平面图形,记为四边形ABCD (按顺时针或逆时针方向书写). 图1 图2 图3 图2是由不在同一直线上的5条线段首尾顺次连结组成的平面图形,记为五边形ABCDE. (2)教师引导,归纳得出: 一般地,由n条(n≥3)不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,又称多边形. (3)活动:根据多边形定义,画一些多边形,同桌相互识别,判断是几边形. 注意:一般以顺时针或逆时针方向按顺序确定顶点字母. (4)观察课本第83页图9.2.1和旁边的图,思考这两组图形有什么不同. 教师点评:都是多边形,但旁边的图不是我们现在研究的范围.指出凸多边形与凹多边形的区别. (5)仿照正三角形的定义,给正多边形下定义. 教师活动:点评,同时强调各边都相等,并且各角都相等的多边形才是正多边形.如正三角形、正四边形(正方形)、正五边形等. (6)阅读课本第83页至84页内容,完成下表. 定义边及条数内角及个数外角及个数对角线及条数三角形四边形多边形
教师指导、点评.(与三角形类似,如图,∠A,∠D,∠C,∠ABC是四边形ABCD的四个内角,延长AB,CB得四边形ABCD的两个外角∠CBE和∠ABF,这两个外角是对顶角) 2.多边形的内角和 问题:三角形的内角和随三角形的形状大小而变化吗? 类比猜想:四边形的内角和随四边形的形状大小而变化吗? 怎样把四边形转化为三角形来计算呢? 思考:通过作对角线可以把四边形转化为三角形吗? 用类比的办法观察,过多边形的一个顶点能作多少条对角线?把多边形分成多少个三角形?填表. 多边形的边数34567…n分成三角形的个数12多边形的内角和
归纳得出:n边形的内角和为 (n-2)·180°. 例1 求八边形的内角和. 【解】 八边形的内角和为 (n2)× 180(82)×180=1 080. 【总结】 n边形的内角和为 (n-2)·180°. 例2 已知一个多边形的内角和为2 160,求这个多边形的边数. 【解】设这个多边形是n边形,根据题意,得 180·(n-2)2 160, 解得 n14, 即这个多边形的边数为14. 【总结】已知多边形内角和求边数时,一般是设出多边形的边数,根据多边形内角和公式列方程求解. 课堂练习 1.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,则这个多边形的内角和为( ) A.540° B.720° C.900° D.1 260° 2.多边形的内角和不可能为( ) A.180° B.540° C.1 080° D.1 200° 3.内角和为720°的多边形是( ) A. B. C. D. 4.若正多边形的一个外角是36°,则该正多边形的内角和为( ) A.360° B.720° C.900° D.1 440° 5.已知正多边形的一个内角是140°,则这个正多边形的边数是( ) A.九 B.八 C.七 D.六 6.如图所示,∠B的值为( ) A.85° B.95° C.105° D.115° 参考答案 1.C 2.D 3.D 4.D 5.A 6.D 课堂小结 1.多边形的相关名称及概念. 2.多边形的内角和定理:n边形的内角和为(n2)·180°. 布置作业 课本第86页练习. 板书设计 第9章 多边形 9.2 多边形的内角和与外角和 第1课时 多边形的内角和 1.多边形的有关概念. 2.多边形的内角和:n边形的内角和为 (n-2)·180°. 例1 例2 教学反思 教学反思 教学反思 教学反思
9.2 多边形的内角和与外角和
第1课时 多边形的内角和
教学目标 1.使学生了解多边形、正多边形及多边形的内角、外角、对角线等概念. 2.使学生通过不同方法探索多边形的内角和公式,并会利用它们进行有关计算. 3.通过把多边形转化为三角形,体会转化思想在几何中的运用,让学生体会从特殊到一般的认识问题的方法. 教学重难点 重点: 探索多边形的内角和公式,应用多边形内角和解决有关的问题. 难点:多边形的内角和公式的推导. 教学过程 导入新课 某小区健身广场中心的边缘是一个五边形(如图),你能求出它的五个内角的和吗? 探究新知 合作探究 1.多边形的有关概念 (1)我们已经知道三角形的定义,那么能否模仿三角形的定义来给四边形、五边形下定义? 教师活动:鼓励、点评. 如图1是由不在同一直线上的4条线段首尾顺次连结组成的平面图形,记为四边形ABCD (按顺时针或逆时针方向书写). 图1 图2 图3 图2是由不在同一直线上的5条线段首尾顺次连结组成的平面图形,记为五边形ABCDE. (2)教师引导,归纳得出: 一般地,由n条(n≥3)不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,又称多边形. (3)活动:根据多边形定义,画一些多边形,同桌相互识别,判断是几边形. 注意:一般以顺时针或逆时针方向按顺序确定顶点字母. (4)观察课本第83页图9.2.1和旁边的图,思考这两组图形有什么不同. 教师点评:都是多边形,但旁边的图不是我们现在研究的范围.指出凸多边形与凹多边形的区别. (5)仿照正三角形的定义,给正多边形下定义. 教师活动:点评,同时强调各边都相等,并且各角都相等的多边形才是正多边形.如正三角形、正四边形(正方形)、正五边形等. (6)阅读课本第83页至84页内容,完成下表. 定义边及条数内角及个数外角及个数对角线及条数三角形四边形多边形
教师指导、点评.(与三角形类似,如图,∠A,∠D,∠C,∠ABC是四边形ABCD的四个内角,延长AB,CB得四边形ABCD的两个外角∠CBE和∠ABF,这两个外角是对顶角) 2.多边形的内角和 问题:三角形的内角和随三角形的形状大小而变化吗? 类比猜想:四边形的内角和随四边形的形状大小而变化吗? 怎样把四边形转化为三角形来计算呢? 思考:通过作对角线可以把四边形转化为三角形吗? 用类比的办法观察,过多边形的一个顶点能作多少条对角线?把多边形分成多少个三角形?填表. 多边形的边数34567…n分成三角形的个数12多边形的内角和
归纳得出:n边形的内角和为 (n-2)·180°. 例1 求八边形的内角和. 【解】 八边形的内角和为 (n2)× 180(82)×180=1 080. 【总结】 n边形的内角和为 (n-2)·180°. 例2 已知一个多边形的内角和为2 160,求这个多边形的边数. 【解】设这个多边形是n边形,根据题意,得 180·(n-2)2 160, 解得 n14, 即这个多边形的边数为14. 【总结】已知多边形内角和求边数时,一般是设出多边形的边数,根据多边形内角和公式列方程求解. 课堂练习 1.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,则这个多边形的内角和为( ) A.540° B.720° C.900° D.1 260° 2.多边形的内角和不可能为( ) A.180° B.540° C.1 080° D.1 200° 3.内角和为720°的多边形是( ) A. B. C. D. 4.若正多边形的一个外角是36°,则该正多边形的内角和为( ) A.360° B.720° C.900° D.1 440° 5.已知正多边形的一个内角是140°,则这个正多边形的边数是( ) A.九 B.八 C.七 D.六 6.如图所示,∠B的值为( ) A.85° B.95° C.105° D.115° 参考答案 1.C 2.D 3.D 4.D 5.A 6.D 课堂小结 1.多边形的相关名称及概念. 2.多边形的内角和定理:n边形的内角和为(n2)·180°. 布置作业 课本第86页练习. 板书设计 第9章 多边形 9.2 多边形的内角和与外角和 第1课时 多边形的内角和 1.多边形的有关概念. 2.多边形的内角和:n边形的内角和为 (n-2)·180°. 例1 例2 教学反思 教学反思 教学反思 教学反思
