21.2一次函数的图像和性质(第2课时一次函数的性质)教学课件--冀教版数学八年级(下)
文档属性
| 名称 | 21.2一次函数的图像和性质(第2课时一次函数的性质)教学课件--冀教版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 721.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:23:49 | ||
图片预览






文档简介
(共20张PPT)
第二十一章 一次函数
第2课时 一次函数的性质
第二十一章 一次函数
21.2 一次函数的图像和性质
学 习 目 标
1、掌握一次函数的性质.(重点)
2、能灵活运用一次函数的图象与性质解答有关问题.(难点)
1.一次函数图象有什么特点?
2.作出一次函数图象需要描出几个点?
只需要描出2个点.
一次函数y=kx+b的图象是一条直线,直线上所有点的坐标都满足表达式y=kx+b.
一般选直线与两坐标轴的两交点,即(0,b)和( ,0).
新课导入
复习
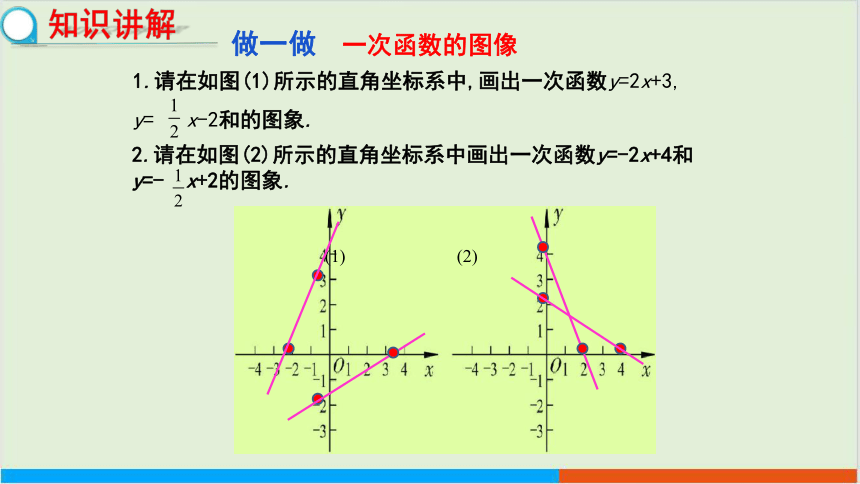
做一做 一次函数的图像
1.请在如图(1)所示的直角坐标系中,画出一次函数y=2x+3,
y= x-2和的图象.
(1)
(2)
2.请在如图(2)所示的直角坐标系中画出一次函数y=-2x+4和
y=- x+2的图象.
知识讲解
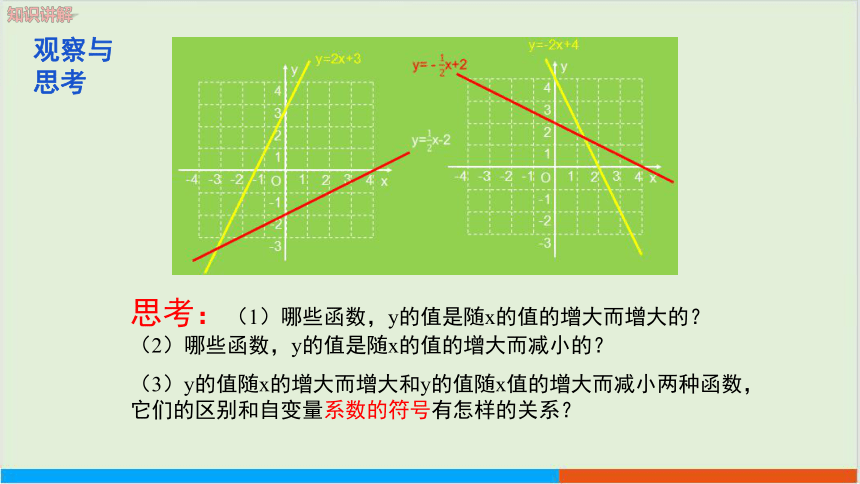
思考:(1)哪些函数,y的值是随x的值的增大而增大的? (2)哪些函数,y的值是随x的值的增大而减小的?
(3)y的值随x的增大而增大和y的值随x值的增大而减小两种函数,它们的区别和自变量系数的符号有怎样的关系?
观察与思考
一般地,我们有:
对于一次函数y=kx+b(k,b为常数,且k≠0):
当k>0时,y的值随x的值的增大而增大;
当k<0时,y的值随x的值的增大而减小.
归纳小结
K决定直线的变化趋势
例1 已知点A(-1,y1),B(2, y2),在函数 y =2x+1 的图像上,则y1、 y2的大小关系是 。
O
x
y
-1
y2
y1
2
变式1:
已知点A(x1,y1),B(x2, y2),在函数 y =2x+1 的图像上,且x1y1变式2:
已知点A(x1,y1),B(x2, y2),在函数 y =-2x+1 的图像上,且x1y1>y2
方法1:解析法:根据一次函数图象的性质: 当k>0时,y随x的增大而增大,因为-1<2,所以y1y1例题讲解
方法2:图像法
1.判断下列函数中,y的值随x的值增大而变化的情况.
(1) y=-3x+3; (2) y=3x-3;
(3) y=(3-π)x; (4) y=0.5x.
解析:
(1)式中,-3<0,所以该函数y的值随x的值增大而减小;
(2)式中,3>0,所以该函数y的值随x的值增大而增大;
(3)式中,3-π<0,所以该函数y的值随x的值增大而减小;
(4)式中,0.5>0,所以该函数y的值随x的值增大而增大.
随堂训练
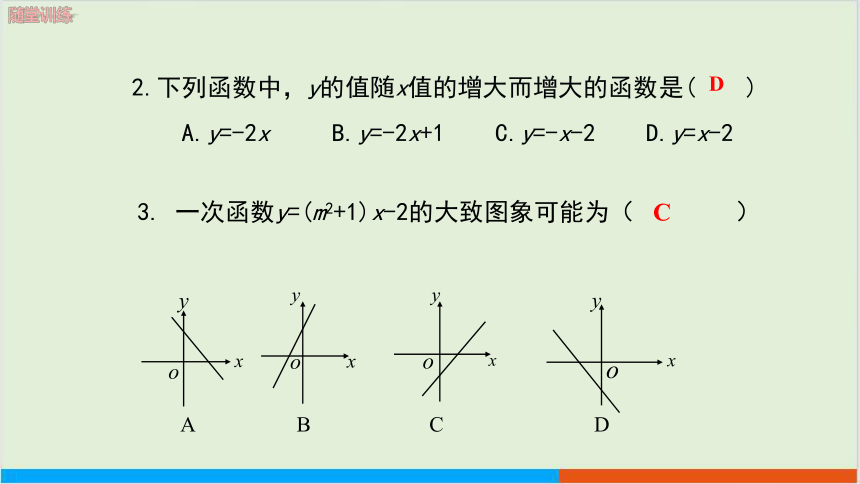
2.下列函数中,y的值随x值的增大而增大的函数是( )
A.y=-2x B.y=-2x+1 C.y=-x-2 D.y=x-2
D
3. 一次函数y=(m2+1)x-2的大致图象可能为( )
C
A B C D
(1)哪些函数的图像与y轴的交点在x轴的上方,哪些函数与y轴的交点在x轴的下方?
(2)函数的图像与y轴的交点在x轴的上方和函数的图像与y轴的交点在x轴的下方,这两种函数,它们的区别与常数项有怎样的关系?
(3)正比例函数的图像一定经过哪个点?
交流
一次函数y=kx+b的图像是经过y轴上的点(0,b)的一条直线.
当b>0时,点(0,b)在x轴的上方;
当b<0时,点(0,b)在x轴的下方;
当b=0时,点(0,0)是原点,即正比例函数y=kx的图像是经过原点的一条直线.
归纳总结
b的正负决定直线与y轴相交的位置
三个一次函数的大致图象如图所示,试分别确定k和b的符号:
k 0,b 0 k 0,b 0 k 0,b 0
<
>
>
<
<
=
我会做
例2.已知关于x的一次函数y=(2k-1)x+(2k+1).
(1)当k满足什么条件时,函数y的值随x的值的增大而增大?
(2)当k满足什么条件时,y=(2k-1)x+(2k+1)的图像经过原点?
(3)当k满足什么条件时,函数y=(2k-1)x+(2k+1)的图像与y轴的交点在x轴的下方?
(4)当k满足什么条件时,函数y的值随x的值的增大而减小且函数图像与y轴的交点在x轴的上方?
例题讲解
解: (1)当2k-1>0时,y的值随x的值增大而增大.解2k-1>0,得k>0.5.
(2)当2k+1=0,即k=-0.5时,函数y=(2k-1)x+(2k+1)的图像经过原点.
(3)当2k+1<0,函数y=(2k-1)x+(2k+1)的图像与y轴的交点在x轴的下方.解2k+1<0,得k<-0.5.
(4)当2k-1<0时,y的值随x的值增大而减小.解得k <0.5.
当2k+1> 0,函数y=(2k-1)x+(2k+1)的图像与y轴的交点在x轴的上方.解得k> -0.5.
所以此时k的取值范围为(-0.5,0.5).
已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数值y 随x的增大而增大且函数图象与y 轴的负半轴相交。
随堂训练
解:(1)由题意得1-2m>0,解得
(2)由题意得1-2m≠0且m-1<0,即
(3)由题意得1-2m>0且m-1<0,即
一次函数的图像与性质
请把下表补充完整.
一次函数 y=kx+b(k≠0) k、b的符号 k>0 k<0 b>0 b<0 b>0 b<0
图像
经过的象限
性质 y随x的增大而 y随x的增大而 一、三、四
一、二、四
二、三、四
增大
减小
一、二、三
拓展
1.正比例函数y=(2k+1)x,若y随x的增大而减小,则k的取值范围是( )
A.k>- B.k<- C.k=- D.k=0
2.一次函数y=-2x+3的图像不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.关于直线L:y=kx+k(k≠0),下列说法不正确的是 ( )
A.点(0,k)在L上 B.L经过定点(-1,0)
C.当k>0时,y随x的增大而增大
D.L经过第一、二、三象限
当堂检测
B
C
D
4.某一次函数的图像经过点(-1,2),且函数y的值随自变量x的增大而减小,则下列函数符合条件的是 ( )
A.y=4x+6 B.y=-x C.y=-x+1 D.y=-3x+5
5.一次函数y=kx+b(k>0,b>0)的图像可能是下图中的( )
C
A
k的正负
b的正负
课堂小结
一次函数的性质
决定函数的变化趋势
决定与y轴的交点位置
共同决定函数经过哪些象限
第二十一章 一次函数
第2课时 一次函数的性质
第二十一章 一次函数
21.2 一次函数的图像和性质
学 习 目 标
1、掌握一次函数的性质.(重点)
2、能灵活运用一次函数的图象与性质解答有关问题.(难点)
1.一次函数图象有什么特点?
2.作出一次函数图象需要描出几个点?
只需要描出2个点.
一次函数y=kx+b的图象是一条直线,直线上所有点的坐标都满足表达式y=kx+b.
一般选直线与两坐标轴的两交点,即(0,b)和( ,0).
新课导入
复习
做一做 一次函数的图像
1.请在如图(1)所示的直角坐标系中,画出一次函数y=2x+3,
y= x-2和的图象.
(1)
(2)
2.请在如图(2)所示的直角坐标系中画出一次函数y=-2x+4和
y=- x+2的图象.
知识讲解
思考:(1)哪些函数,y的值是随x的值的增大而增大的? (2)哪些函数,y的值是随x的值的增大而减小的?
(3)y的值随x的增大而增大和y的值随x值的增大而减小两种函数,它们的区别和自变量系数的符号有怎样的关系?
观察与思考
一般地,我们有:
对于一次函数y=kx+b(k,b为常数,且k≠0):
当k>0时,y的值随x的值的增大而增大;
当k<0时,y的值随x的值的增大而减小.
归纳小结
K决定直线的变化趋势
例1 已知点A(-1,y1),B(2, y2),在函数 y =2x+1 的图像上,则y1、 y2的大小关系是 。
O
x
y
-1
y2
y1
2
变式1:
已知点A(x1,y1),B(x2, y2),在函数 y =2x+1 的图像上,且x1
已知点A(x1,y1),B(x2, y2),在函数 y =-2x+1 的图像上,且x1
方法1:解析法:根据一次函数图象的性质: 当k>0时,y随x的增大而增大,因为-1<2,所以y1
方法2:图像法
1.判断下列函数中,y的值随x的值增大而变化的情况.
(1) y=-3x+3; (2) y=3x-3;
(3) y=(3-π)x; (4) y=0.5x.
解析:
(1)式中,-3<0,所以该函数y的值随x的值增大而减小;
(2)式中,3>0,所以该函数y的值随x的值增大而增大;
(3)式中,3-π<0,所以该函数y的值随x的值增大而减小;
(4)式中,0.5>0,所以该函数y的值随x的值增大而增大.
随堂训练
2.下列函数中,y的值随x值的增大而增大的函数是( )
A.y=-2x B.y=-2x+1 C.y=-x-2 D.y=x-2
D
3. 一次函数y=(m2+1)x-2的大致图象可能为( )
C
A B C D
(1)哪些函数的图像与y轴的交点在x轴的上方,哪些函数与y轴的交点在x轴的下方?
(2)函数的图像与y轴的交点在x轴的上方和函数的图像与y轴的交点在x轴的下方,这两种函数,它们的区别与常数项有怎样的关系?
(3)正比例函数的图像一定经过哪个点?
交流
一次函数y=kx+b的图像是经过y轴上的点(0,b)的一条直线.
当b>0时,点(0,b)在x轴的上方;
当b<0时,点(0,b)在x轴的下方;
当b=0时,点(0,0)是原点,即正比例函数y=kx的图像是经过原点的一条直线.
归纳总结
b的正负决定直线与y轴相交的位置
三个一次函数的大致图象如图所示,试分别确定k和b的符号:
k 0,b 0 k 0,b 0 k 0,b 0
<
>
>
<
<
=
我会做
例2.已知关于x的一次函数y=(2k-1)x+(2k+1).
(1)当k满足什么条件时,函数y的值随x的值的增大而增大?
(2)当k满足什么条件时,y=(2k-1)x+(2k+1)的图像经过原点?
(3)当k满足什么条件时,函数y=(2k-1)x+(2k+1)的图像与y轴的交点在x轴的下方?
(4)当k满足什么条件时,函数y的值随x的值的增大而减小且函数图像与y轴的交点在x轴的上方?
例题讲解
解: (1)当2k-1>0时,y的值随x的值增大而增大.解2k-1>0,得k>0.5.
(2)当2k+1=0,即k=-0.5时,函数y=(2k-1)x+(2k+1)的图像经过原点.
(3)当2k+1<0,函数y=(2k-1)x+(2k+1)的图像与y轴的交点在x轴的下方.解2k+1<0,得k<-0.5.
(4)当2k-1<0时,y的值随x的值增大而减小.解得k <0.5.
当2k+1> 0,函数y=(2k-1)x+(2k+1)的图像与y轴的交点在x轴的上方.解得k> -0.5.
所以此时k的取值范围为(-0.5,0.5).
已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数值y 随x的增大而增大且函数图象与y 轴的负半轴相交。
随堂训练
解:(1)由题意得1-2m>0,解得
(2)由题意得1-2m≠0且m-1<0,即
(3)由题意得1-2m>0且m-1<0,即
一次函数的图像与性质
请把下表补充完整.
一次函数 y=kx+b(k≠0) k、b的符号 k>0 k<0 b>0 b<0 b>0 b<0
图像
经过的象限
性质 y随x的增大而 y随x的增大而 一、三、四
一、二、四
二、三、四
增大
减小
一、二、三
拓展
1.正比例函数y=(2k+1)x,若y随x的增大而减小,则k的取值范围是( )
A.k>- B.k<- C.k=- D.k=0
2.一次函数y=-2x+3的图像不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.关于直线L:y=kx+k(k≠0),下列说法不正确的是 ( )
A.点(0,k)在L上 B.L经过定点(-1,0)
C.当k>0时,y随x的增大而增大
D.L经过第一、二、三象限
当堂检测
B
C
D
4.某一次函数的图像经过点(-1,2),且函数y的值随自变量x的增大而减小,则下列函数符合条件的是 ( )
A.y=4x+6 B.y=-x C.y=-x+1 D.y=-3x+5
5.一次函数y=kx+b(k>0,b>0)的图像可能是下图中的( )
C
A
k的正负
b的正负
课堂小结
一次函数的性质
决定函数的变化趋势
决定与y轴的交点位置
共同决定函数经过哪些象限
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
