6.4.2 多边形的内角和与外角和 教学课件 --北师大版初中数学八年级(下)
文档属性
| 名称 | 6.4.2 多边形的内角和与外角和 教学课件 --北师大版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:00 | ||
图片预览






文档简介
(共15张PPT)
第六章 平行四边形
6.4.2多边形的内角和与外角和
第六章 平行四边形
学 习 目 标
1.了解多边形的外角定义,并能准确找出多边形的外角;(重点)
2.掌握多边形的外角和公式,能利用内角和与 外角和公式解决实际问题.(难点)
1、七边形内角和为( )
900°
2、十边形内角和为( )
1440°
3、多边形内角和为1260°则它是
( )边形。
九
4、多边形内角和为1800°则它是
( )边形。
十二
知识回顾
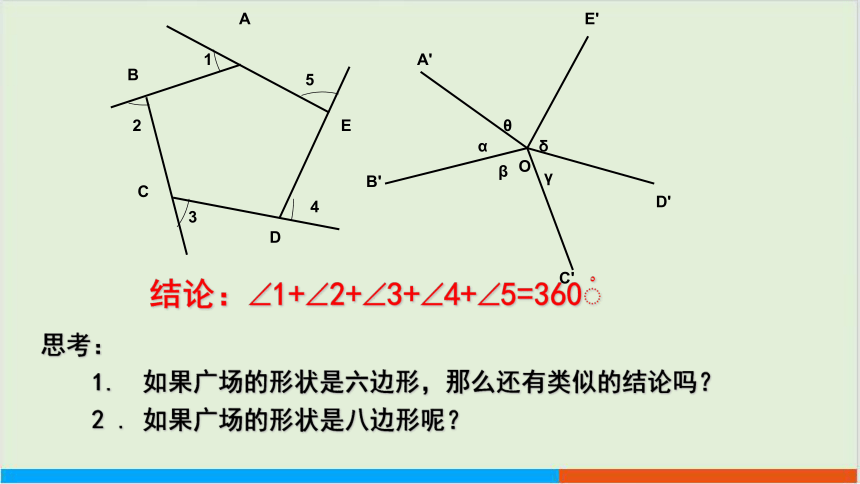
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。
情景导入
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出 1+ 2+ 3+ 4+ 5的结果吗?你是怎样得到的?
合作探究
结论: 1+ 2+ 3+ 4+ 5=360
C'
A
B
C
D
E
A'
D'
E'
B'
O
β
γ
δ
θ
α
1
2
3
4
5
思考:
1. 如果广场的形状是六边形,那么还有类似的结论吗?
2 . 如果广场的形状是八边形呢?
1.多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
2.在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。
知识讲解
多边形的外角和等于多少?
方法Ⅰ:类似探究多边形的内角和的方法,由三角形、四边形、五边形…的外角和开始探究;
方法Ⅱ:由n边形的内角和等于(n-2)·180°出发,探究问题。
多边形的外角和等于360°
例2.一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是
(n-2)·180°,外角和等于360°,
所以(n-2)·180 °=3×360 °
解得:n=8
答:这个多边形是八边形.
例题讲解
1、一个多边形的外角和是内角和的一半,则它的边数是( )
A、7 B、6 C、4 D、5
2、如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )
A、110° B、108° C、105° D、100°
B
D
随堂训练
3. 一个多边形的外角都等于60°,这个多边形是几边形
4.下图是三个完全相同的正多边形拼成的无缝隙、不重叠的图形的一部分,这种多边形是几边形?为什么?
1.多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
2.在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。
3.多边形的外角和等于360°
课堂小结
1、一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数是( )
A、5 B、6 C、7 D、8
2、n边形的每个外角都等于45°,则n=______.
当堂检测
3.已知多边形的内角和与某一个外角的度数总和为1350o, 求多边形的边数.
4.一个多边形减少一个内角后的度数和为2300°.
(1)求它的边数.
(2)求减少的那个内角的度数.
第六章 平行四边形
6.4.2多边形的内角和与外角和
第六章 平行四边形
学 习 目 标
1.了解多边形的外角定义,并能准确找出多边形的外角;(重点)
2.掌握多边形的外角和公式,能利用内角和与 外角和公式解决实际问题.(难点)
1、七边形内角和为( )
900°
2、十边形内角和为( )
1440°
3、多边形内角和为1260°则它是
( )边形。
九
4、多边形内角和为1800°则它是
( )边形。
十二
知识回顾
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。
情景导入
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出 1+ 2+ 3+ 4+ 5的结果吗?你是怎样得到的?
合作探究
结论: 1+ 2+ 3+ 4+ 5=360
C'
A
B
C
D
E
A'
D'
E'
B'
O
β
γ
δ
θ
α
1
2
3
4
5
思考:
1. 如果广场的形状是六边形,那么还有类似的结论吗?
2 . 如果广场的形状是八边形呢?
1.多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
2.在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。
知识讲解
多边形的外角和等于多少?
方法Ⅰ:类似探究多边形的内角和的方法,由三角形、四边形、五边形…的外角和开始探究;
方法Ⅱ:由n边形的内角和等于(n-2)·180°出发,探究问题。
多边形的外角和等于360°
例2.一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是
(n-2)·180°,外角和等于360°,
所以(n-2)·180 °=3×360 °
解得:n=8
答:这个多边形是八边形.
例题讲解
1、一个多边形的外角和是内角和的一半,则它的边数是( )
A、7 B、6 C、4 D、5
2、如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是( )
A、110° B、108° C、105° D、100°
B
D
随堂训练
3. 一个多边形的外角都等于60°,这个多边形是几边形
4.下图是三个完全相同的正多边形拼成的无缝隙、不重叠的图形的一部分,这种多边形是几边形?为什么?
1.多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
2.在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。
3.多边形的外角和等于360°
课堂小结
1、一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数是( )
A、5 B、6 C、7 D、8
2、n边形的每个外角都等于45°,则n=______.
当堂检测
3.已知多边形的内角和与某一个外角的度数总和为1350o, 求多边形的边数.
4.一个多边形减少一个内角后的度数和为2300°.
(1)求它的边数.
(2)求减少的那个内角的度数.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
