1.2 直角三角形(第1课时) 教学课件 --北师大版初中数学八年级(下)
文档属性
| 名称 | 1.2 直角三角形(第1课时) 教学课件 --北师大版初中数学八年级(下) |  | |
| 格式 | ppt | ||
| 文件大小 | 800.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:00 | ||
图片预览






文档简介
(共25张PPT)
第 一章 三角形的证明
第一章 三角形的证明
1.了解勾股定理及其逆定理的证明方法.(重点)
2.结合具体例子了解逆命题的概念,识别两个互逆命题,知道原命题成立,其逆命题不一定成立.(难点)
学 习 目 标
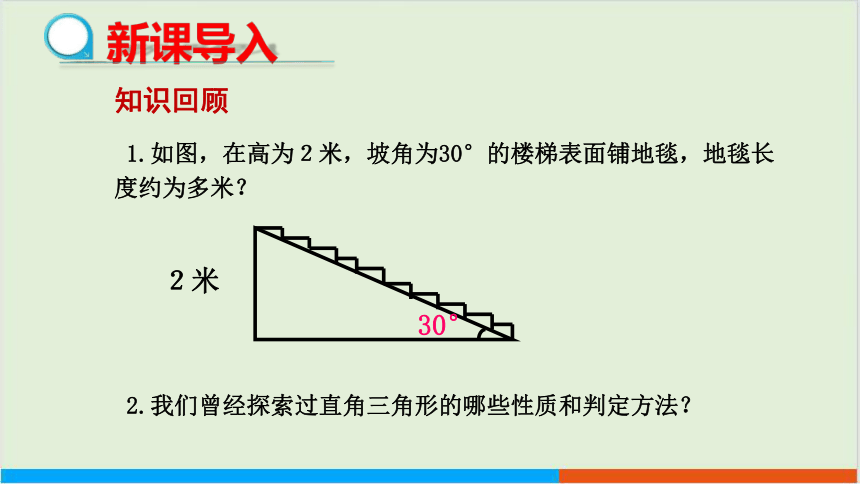
1.如图,在高为2米,坡角为30°的楼梯表面铺地毯,地毯长度约为多米?
30°
2米
2.我们曾经探索过直角三角形的哪些性质和判定方法?
新课导入
知识回顾
3.直角三角形的边有哪些性质?
一般性质:直角三角形的边具有一般三角
形的所有性质.
特殊性质:在直角三角形中,如果一个锐
角等于30,那么它所对的直角
边等于斜边的一半.
1.直角三角形的角有哪些性质?
2.直角三角形的边有哪些性质?
3.如果一个三角形有两个锐角互余,那么这个三角形是直角三角形吗?为什么?
思考
阅读课本14-18页,回答问题:
1.什么是直角三角形?
2.直角三角形的角有哪些性质?反之,任意一个三角形的两锐角具备这种关系就是直角三角形吗?请说明理由。
3.直角三角形的边有哪些性质?勾股定理内容是什么?反之,在一个三角形中,当两边的平方和等于第三边的平方时,这个三角形是直角三角形吗?请说明理由。
4.逆命题、逆定理的概念是什么?两个互逆命题、互逆定理的关系是什么?真命题的逆命题是真命题吗?定理的逆命题也是定理吗?
勾股定理:如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.勾股定理在西方文献中又称为毕达哥拉斯定理
知识讲解
1.勾股定理
c
a
b
c
a
b
c
a
b
c
a
b
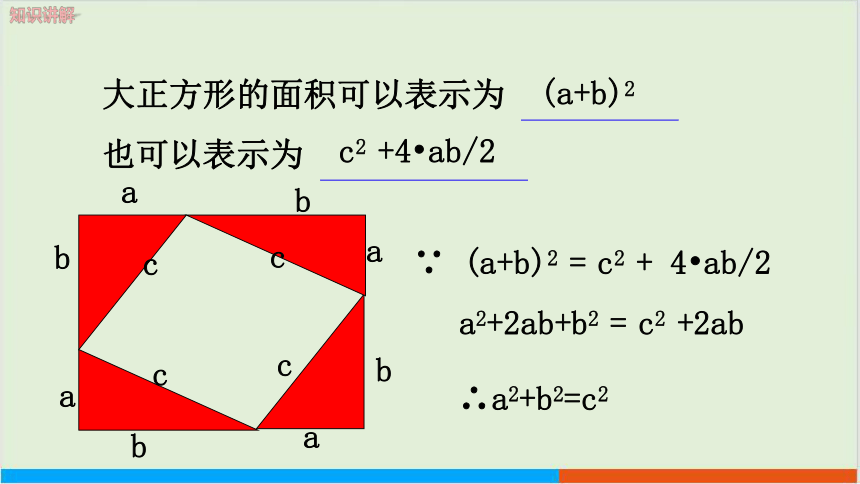
∵ (a+b)2 = c2 + 4 ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为
也可以表示为
(a+b)2
c2 +4 ab/2
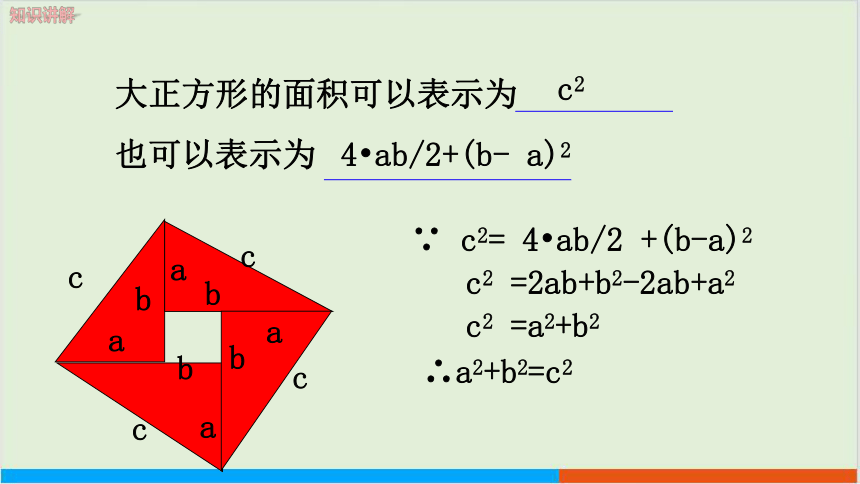
∵ c2= 4 ab/2 +(b-a)2
c2 =2ab+b2-2ab+a2
c2 =a2+b2
∴a2+b2=c2
大正方形的面积可以表示为
也可以表示为
c2
4 ab/2+(b- a)2
c
a
b
c
a
b
c
a
b
c
b
a
勾股定理:直角三角形两条直角边的平方和等于斜边的平方。
反过来:如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
提问:这个命题的条件是什么?结论是什么?请你根据条件和结论写出已知和求证.
已知:如图(1),在△ABC中, AB2+AC2=BC2.
求证:△ABC是直角三角形.
A
B
C
图(1)
A
B
C
图(1)
A′
B′
C′
图(2)
证明:如图(2)作Rt△A′B′C′,使∠A′=90°, A′B′=AB,A′C′=AC,
A′B′2+A′C′2=B′C′2(勾股定理).
∵AB2+AC2=BC2 ,
∴BC2=B′C′2.
∴BC=B′C′.
∴△ABC≌△A′B′C′(SSS).
∴∠A==∠A′=90°(全等三角形的对应角相等).
即,△ABC是直角三角形.
定理: 直角三角形两条直角边的平方
和等于斜边的平方。
定理: 如果三角形两边的平方和等于第三边的平方,那么这个三形是直角三角形。
两个定理的条件和结论有什么样的关系?
议一议
观 察
如果两个角是对顶角,那么他们相等;
如果两个角相等,那么它们是对顶角。
一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等。
如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎。
以上两个命题的条件和结论有类似的关系吗?
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
2.互逆命题
你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗
它们都是真命题吗
思考:
说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果ab=0,那么a=0,b=0.
提问:一个命题是真命题,它的逆命题一定是真命题吗?
一个命题是真命题,它逆命题却不一定是真命题.
你还能举出一些例子吗
想一想:互逆命题与互逆定理有何关系
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
3.互逆定理
判断正误:
(1)互逆命题一定是互逆定理;
(2)互逆定理一定是互逆命题.
我们已经学习了一些互逆定理,如勾股定理及其逆定理、“两直线平行,内错角相等与“内错角相等,两直线平行”等.请你再举出一些互逆定理的例子.
1.写出下列命题的逆命题,并判断每对命题的真假:
(2)矩形是正方形;
(3)如果x2﹥0,那么x﹥0;
(4)直角都相等.
当堂检测
2.已知:线段a∶b∶c的值如下,则能够组成直角三角形的是( )
(A)3∶4∶6 (B)5∶12∶13
(C)1∶2∶4 (4)1∶3∶5
B
3.在△ABC中,已知,AB=13cm,BC=10cm,BC边上的中线AD=12cm ,
求证:AB=AC
4.已知:在△ABC中, ∠ C=900, AD是BC边上的中线,DE⊥AB,垂足为E,
求证:AC2=AE2-BE2
解后反思
证明线段的平方和或差,常常考虑运用勾股定理,若无直角三角形,可通过作垂线构造直角三角形,以便运用勾股定理。
互逆命题
定理:有两个锐角互余的三角形是直角三角形.
勾股定理:直角三角形两直角边的平方和等于 斜边的平方.
定理: 如果三角形两边的平方和等于第三边的平方,那么这个三形是直角三角形。
定理:直角三角形两锐角互余.
互逆定理
课堂小结
第 一章 三角形的证明
第一章 三角形的证明
1.了解勾股定理及其逆定理的证明方法.(重点)
2.结合具体例子了解逆命题的概念,识别两个互逆命题,知道原命题成立,其逆命题不一定成立.(难点)
学 习 目 标
1.如图,在高为2米,坡角为30°的楼梯表面铺地毯,地毯长度约为多米?
30°
2米
2.我们曾经探索过直角三角形的哪些性质和判定方法?
新课导入
知识回顾
3.直角三角形的边有哪些性质?
一般性质:直角三角形的边具有一般三角
形的所有性质.
特殊性质:在直角三角形中,如果一个锐
角等于30,那么它所对的直角
边等于斜边的一半.
1.直角三角形的角有哪些性质?
2.直角三角形的边有哪些性质?
3.如果一个三角形有两个锐角互余,那么这个三角形是直角三角形吗?为什么?
思考
阅读课本14-18页,回答问题:
1.什么是直角三角形?
2.直角三角形的角有哪些性质?反之,任意一个三角形的两锐角具备这种关系就是直角三角形吗?请说明理由。
3.直角三角形的边有哪些性质?勾股定理内容是什么?反之,在一个三角形中,当两边的平方和等于第三边的平方时,这个三角形是直角三角形吗?请说明理由。
4.逆命题、逆定理的概念是什么?两个互逆命题、互逆定理的关系是什么?真命题的逆命题是真命题吗?定理的逆命题也是定理吗?
勾股定理:如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.勾股定理在西方文献中又称为毕达哥拉斯定理
知识讲解
1.勾股定理
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 + 4 ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为
也可以表示为
(a+b)2
c2 +4 ab/2
∵ c2= 4 ab/2 +(b-a)2
c2 =2ab+b2-2ab+a2
c2 =a2+b2
∴a2+b2=c2
大正方形的面积可以表示为
也可以表示为
c2
4 ab/2+(b- a)2
c
a
b
c
a
b
c
a
b
c
b
a
勾股定理:直角三角形两条直角边的平方和等于斜边的平方。
反过来:如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
提问:这个命题的条件是什么?结论是什么?请你根据条件和结论写出已知和求证.
已知:如图(1),在△ABC中, AB2+AC2=BC2.
求证:△ABC是直角三角形.
A
B
C
图(1)
A
B
C
图(1)
A′
B′
C′
图(2)
证明:如图(2)作Rt△A′B′C′,使∠A′=90°, A′B′=AB,A′C′=AC,
A′B′2+A′C′2=B′C′2(勾股定理).
∵AB2+AC2=BC2 ,
∴BC2=B′C′2.
∴BC=B′C′.
∴△ABC≌△A′B′C′(SSS).
∴∠A==∠A′=90°(全等三角形的对应角相等).
即,△ABC是直角三角形.
定理: 直角三角形两条直角边的平方
和等于斜边的平方。
定理: 如果三角形两边的平方和等于第三边的平方,那么这个三形是直角三角形。
两个定理的条件和结论有什么样的关系?
议一议
观 察
如果两个角是对顶角,那么他们相等;
如果两个角相等,那么它们是对顶角。
一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等。
如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎。
以上两个命题的条件和结论有类似的关系吗?
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
2.互逆命题
你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗
它们都是真命题吗
思考:
说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果ab=0,那么a=0,b=0.
提问:一个命题是真命题,它的逆命题一定是真命题吗?
一个命题是真命题,它逆命题却不一定是真命题.
你还能举出一些例子吗
想一想:互逆命题与互逆定理有何关系
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
3.互逆定理
判断正误:
(1)互逆命题一定是互逆定理;
(2)互逆定理一定是互逆命题.
我们已经学习了一些互逆定理,如勾股定理及其逆定理、“两直线平行,内错角相等与“内错角相等,两直线平行”等.请你再举出一些互逆定理的例子.
1.写出下列命题的逆命题,并判断每对命题的真假:
(2)矩形是正方形;
(3)如果x2﹥0,那么x﹥0;
(4)直角都相等.
当堂检测
2.已知:线段a∶b∶c的值如下,则能够组成直角三角形的是( )
(A)3∶4∶6 (B)5∶12∶13
(C)1∶2∶4 (4)1∶3∶5
B
3.在△ABC中,已知,AB=13cm,BC=10cm,BC边上的中线AD=12cm ,
求证:AB=AC
4.已知:在△ABC中, ∠ C=900, AD是BC边上的中线,DE⊥AB,垂足为E,
求证:AC2=AE2-BE2
解后反思
证明线段的平方和或差,常常考虑运用勾股定理,若无直角三角形,可通过作垂线构造直角三角形,以便运用勾股定理。
互逆命题
定理:有两个锐角互余的三角形是直角三角形.
勾股定理:直角三角形两直角边的平方和等于 斜边的平方.
定理: 如果三角形两边的平方和等于第三边的平方,那么这个三形是直角三角形。
定理:直角三角形两锐角互余.
互逆定理
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
