22.1平行四边形的性质(第1课时)教学课件--冀教版数学八年级(下)
文档属性
| 名称 | 22.1平行四边形的性质(第1课时)教学课件--冀教版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:23:49 | ||
图片预览






文档简介
(共23张PPT)
第二十二章 四边形
第二十二章 四边形
22.1 平行四边形的性质
第1课时
学 习 目 标
1、理解平行四边形的定义及有关概念.(重点)
2、通过旋转等操作活动体会平行四边形的中心对称性,并体会平移、中心对称等图形变化在研究平行四边形及其性质中的运用.
3、探索并掌握平行四边形的对边相等、对角相等的性质.(难点)
在数学的天地里,重要的不是我们知道什么,
更重要的是我们应该
怎么知道什么。
——毕达哥拉斯
新课导入
在我们的周围存在着许多四边形.观察下列图片,
从中找出四边形,并就它们的共同特性和不同特性,
和大家交流你的看法.
教室 瓷砖图案 伸缩门 晾衣架
上面图片中的四边形可以归类为以下四种:
观察图形,以上图形边的位置有什么特征?
两组对边分别平行
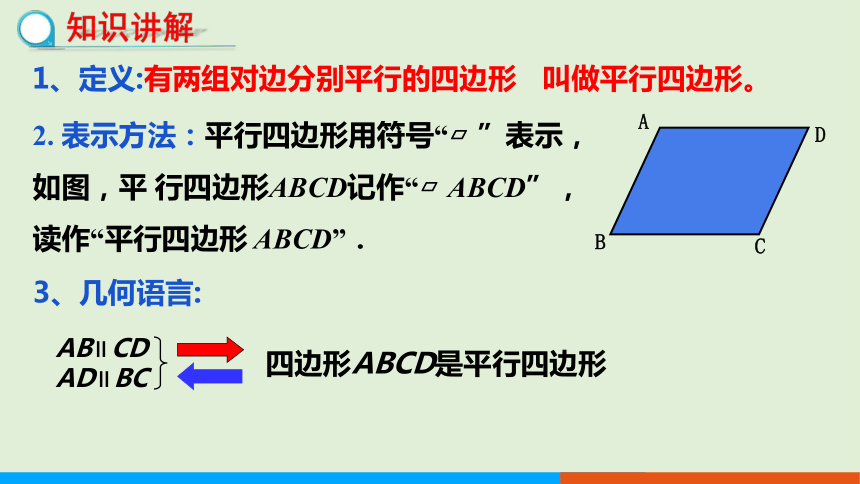
1、定义:有两组对边分别平行的四边形 叫做平行四边形。
3、几何语言:
四边形ABCD是平行四边形
AB∥CD
AD∥BC
A
B
C
D
2. 表示方法:平行四边形用符号“ ”表示,
如图,平 行四边形ABCD记作“ ABCD”,
读作“平行四边形 ABCD”.
知识讲解
A
B
C
D
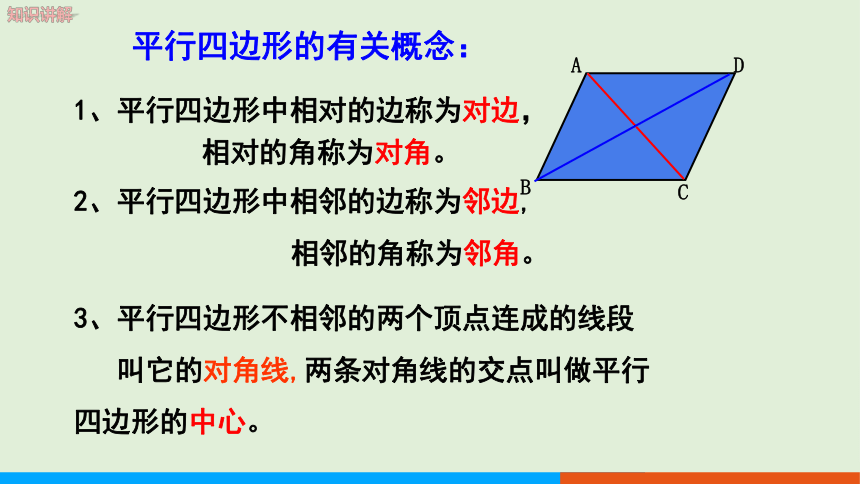
1、平行四边形中相对的边称为对边,
相对的角称为对角。
2、平行四边形中相邻的边称为邻边,
相邻的角称为邻角。
平行四边形的有关概念:
3、平行四边形不相邻的两个顶点连成的线段
叫它的对角线,两条对角线的交点叫做平行 四边形的中心。
C
D
A
B
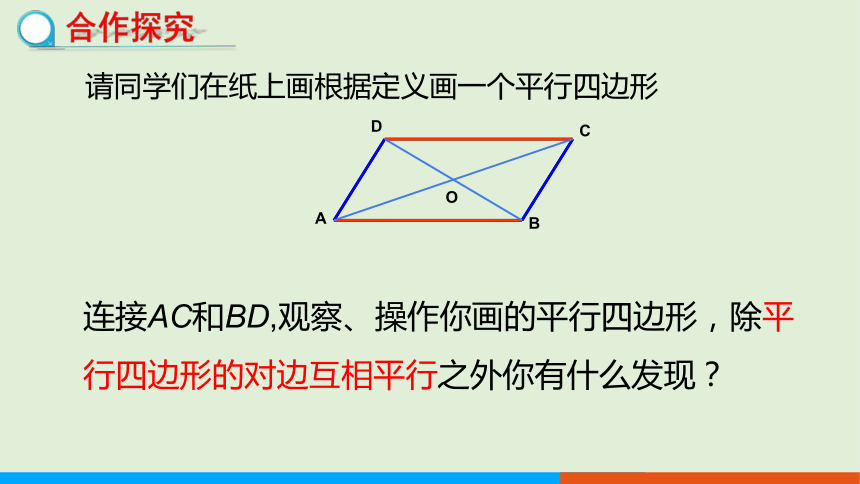
连接AC和BD,观察、操作你画的平行四边形,除平行四边形的对边互相平行之外你有什么发现?
请同学们在纸上画根据定义画一个平行四边形
O
合作探究
一起探究
(1)在半透明的纸上画一个 ABCD,再复制一个,将两个图形完全重合,用大头针钉在中心处,使下面的图形不动,将上面的图形绕中心O旋转180°,这两个图形能完全重合吗 平行四边形是不是中心对称图形 如果是中心对称图形,哪个点是它的对称中心 被对角线分成的三角形中,关于点O成中心对称的图形有几对
●ADOCBDBOCA看一看(1)由演示可得平行四边形是中心对称图形,它的对称中心是两条对角线的交点.
(2)在上面的活动中,你发现了 ABCD的对边AD与CB,AB与CD之间有怎样的数量关系?对角∠BAD与∠DCB,∠ABC与∠CDA之间有怎样的数量关系?线段OA与OC,OB与OD之间有怎样的数量关系?
(3)把你的发现写出来,说明理由,并将结果与大家交流.
知识讲解
我们很容易发现平行四边形的对边相等,对角相等,我们来证明一下.
已知:如图所示,四边形ABCD是平行四边形.
求证:(1)AD=CB,AB=CD.(2)∠BAD=∠DCB,∠ABC=∠CDA.
证明:如图所示,连接BD,在△ABD和△CDB中,
∵AD∥CB,AB∥CD,
∴∠ABD=∠CDB,∠ADB=∠CBD.
又∵BD=DB,
∴△ABD≌△CDB.
∴AD=CB,AB=CD,∠BAD=∠DCB.
∵∠ABD=∠CDB,∠ADB=∠CBD,
∴∠ABD+∠CBD=∠CDB+∠ADB,
即∠ABC=∠CDA.
平行四边形的性质
文字叙述
符号语言
对边平行
∵四边形ABCD是平行四 边形
∴ AB∥DC ,AD∥BC
对边相等
∵四边形ABCD是平行四边形
∴ AB=DC ,AD=BC
关于
边的
性质
A
D
C
B
文字叙述
符号语言
关
于
角
的
性
质
对角相等
邻角互补
∵四边形ABCD是平行四边形
∴ ∠A=∠C ,∠B=∠D
∵四边形ABCD是平行四边形
∴ ∠A +∠ B =180°
∠A +∠D =180 °
∠C +∠ D=180°
∠C+∠ B =180°
平行四边形的性质
A
D
C
B
例1: 如图,在 ABCD中,已知∠B+∠D=260°,求∠A、∠C的度数.
解:
在 ABCD中,∠A=∠C,∠B=∠D.
∵∠B+∠D=260°,
∴∠B=∠D=130°.
∵AD//BC
∴∠C=180°-∠D=180°-130°=50°.
∴∠A=∠C=50°.
例题讲解
1、火眼金睛(对的在括号内填“∨”,错的填“×”)
(1)平行四边形两组对边分别平行. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=35°,
那么∠B=55°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,
那么∠B=145°. ( )
随堂训练
∨
×
∨
∨
×
∨
2、已知:如图所示, ABCD的周长为22 cm,△ABD的周长为18 cm,求对角线BD的长.
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC.
由已知条件,得2(AB+AD)=22,
∴AB+AD=11.
又∵AB+AD+BD=18,
∴BD=18-11=7.
3.如图所示,在 ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.
求证:BC=CF.
证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠ADE=∠FCE.
∵E是CD的中点,∴DE=CE.
在△ADE和△FCE中,
∴△ADE ≌△FCE,∴AD=CF.
∴BC=CF.
平行四边形的性质
对称性:中心对称图形,对称中心是两条对角线的交点
角:对角相等,邻角互补
课堂小结
边:对边平行,对边相等
当堂检测
1、如图,在 ABCD中,BM是∠ABC的平分线,交CD于点M,且MC=2, ABCD的周长是14,则DM等于( )
A.1 B.2 C.3 D.4
2、如图,在 ABCD中,对角线AC的垂直平分线分别交AD,BC于点E,F,连接CE,若△CED的周长为6,则 ABCD的周长为( )
A.6 B.12 C.18 D.24
3、如图,在 ABCD中,CE⊥AB,E为垂足,如果∠A=120°,那么∠BCE的度数
是( )
A.80° B.50° C.40° D.30°
C
B
D
4、在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标分别是A(a,b),B(4,-2),C(-a,-b),则关于点D的说法正确的是( )
甲:点D在第一象限.
乙:点D与点A关于原点对称.
丙:点D的坐标是(-4,2).
丁:点D与原点距离是2 .
A.甲乙 B.丙丁 C.甲丁 D.乙丙
B
5、 已知:如图,在 ABCD 中,E,F分别是BC,AD上的点,且BE=DF.求证AE=CF.
解:
在 ABCD中,AB=CD,
∠B=∠D,
在△ABE和△CDF中,
所以△ABE≌△CDF,所以AE=CF.
第二十二章 四边形
第二十二章 四边形
22.1 平行四边形的性质
第1课时
学 习 目 标
1、理解平行四边形的定义及有关概念.(重点)
2、通过旋转等操作活动体会平行四边形的中心对称性,并体会平移、中心对称等图形变化在研究平行四边形及其性质中的运用.
3、探索并掌握平行四边形的对边相等、对角相等的性质.(难点)
在数学的天地里,重要的不是我们知道什么,
更重要的是我们应该
怎么知道什么。
——毕达哥拉斯
新课导入
在我们的周围存在着许多四边形.观察下列图片,
从中找出四边形,并就它们的共同特性和不同特性,
和大家交流你的看法.
教室 瓷砖图案 伸缩门 晾衣架
上面图片中的四边形可以归类为以下四种:
观察图形,以上图形边的位置有什么特征?
两组对边分别平行
1、定义:有两组对边分别平行的四边形 叫做平行四边形。
3、几何语言:
四边形ABCD是平行四边形
AB∥CD
AD∥BC
A
B
C
D
2. 表示方法:平行四边形用符号“ ”表示,
如图,平 行四边形ABCD记作“ ABCD”,
读作“平行四边形 ABCD”.
知识讲解
A
B
C
D
1、平行四边形中相对的边称为对边,
相对的角称为对角。
2、平行四边形中相邻的边称为邻边,
相邻的角称为邻角。
平行四边形的有关概念:
3、平行四边形不相邻的两个顶点连成的线段
叫它的对角线,两条对角线的交点叫做平行 四边形的中心。
C
D
A
B
连接AC和BD,观察、操作你画的平行四边形,除平行四边形的对边互相平行之外你有什么发现?
请同学们在纸上画根据定义画一个平行四边形
O
合作探究
一起探究
(1)在半透明的纸上画一个 ABCD,再复制一个,将两个图形完全重合,用大头针钉在中心处,使下面的图形不动,将上面的图形绕中心O旋转180°,这两个图形能完全重合吗 平行四边形是不是中心对称图形 如果是中心对称图形,哪个点是它的对称中心 被对角线分成的三角形中,关于点O成中心对称的图形有几对
●ADOCBDBOCA看一看(1)由演示可得平行四边形是中心对称图形,它的对称中心是两条对角线的交点.
(2)在上面的活动中,你发现了 ABCD的对边AD与CB,AB与CD之间有怎样的数量关系?对角∠BAD与∠DCB,∠ABC与∠CDA之间有怎样的数量关系?线段OA与OC,OB与OD之间有怎样的数量关系?
(3)把你的发现写出来,说明理由,并将结果与大家交流.
知识讲解
我们很容易发现平行四边形的对边相等,对角相等,我们来证明一下.
已知:如图所示,四边形ABCD是平行四边形.
求证:(1)AD=CB,AB=CD.(2)∠BAD=∠DCB,∠ABC=∠CDA.
证明:如图所示,连接BD,在△ABD和△CDB中,
∵AD∥CB,AB∥CD,
∴∠ABD=∠CDB,∠ADB=∠CBD.
又∵BD=DB,
∴△ABD≌△CDB.
∴AD=CB,AB=CD,∠BAD=∠DCB.
∵∠ABD=∠CDB,∠ADB=∠CBD,
∴∠ABD+∠CBD=∠CDB+∠ADB,
即∠ABC=∠CDA.
平行四边形的性质
文字叙述
符号语言
对边平行
∵四边形ABCD是平行四 边形
∴ AB∥DC ,AD∥BC
对边相等
∵四边形ABCD是平行四边形
∴ AB=DC ,AD=BC
关于
边的
性质
A
D
C
B
文字叙述
符号语言
关
于
角
的
性
质
对角相等
邻角互补
∵四边形ABCD是平行四边形
∴ ∠A=∠C ,∠B=∠D
∵四边形ABCD是平行四边形
∴ ∠A +∠ B =180°
∠A +∠D =180 °
∠C +∠ D=180°
∠C+∠ B =180°
平行四边形的性质
A
D
C
B
例1: 如图,在 ABCD中,已知∠B+∠D=260°,求∠A、∠C的度数.
解:
在 ABCD中,∠A=∠C,∠B=∠D.
∵∠B+∠D=260°,
∴∠B=∠D=130°.
∵AD//BC
∴∠C=180°-∠D=180°-130°=50°.
∴∠A=∠C=50°.
例题讲解
1、火眼金睛(对的在括号内填“∨”,错的填“×”)
(1)平行四边形两组对边分别平行. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=35°,
那么∠B=55°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,
那么∠B=145°. ( )
随堂训练
∨
×
∨
∨
×
∨
2、已知:如图所示, ABCD的周长为22 cm,△ABD的周长为18 cm,求对角线BD的长.
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC.
由已知条件,得2(AB+AD)=22,
∴AB+AD=11.
又∵AB+AD+BD=18,
∴BD=18-11=7.
3.如图所示,在 ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.
求证:BC=CF.
证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠ADE=∠FCE.
∵E是CD的中点,∴DE=CE.
在△ADE和△FCE中,
∴△ADE ≌△FCE,∴AD=CF.
∴BC=CF.
平行四边形的性质
对称性:中心对称图形,对称中心是两条对角线的交点
角:对角相等,邻角互补
课堂小结
边:对边平行,对边相等
当堂检测
1、如图,在 ABCD中,BM是∠ABC的平分线,交CD于点M,且MC=2, ABCD的周长是14,则DM等于( )
A.1 B.2 C.3 D.4
2、如图,在 ABCD中,对角线AC的垂直平分线分别交AD,BC于点E,F,连接CE,若△CED的周长为6,则 ABCD的周长为( )
A.6 B.12 C.18 D.24
3、如图,在 ABCD中,CE⊥AB,E为垂足,如果∠A=120°,那么∠BCE的度数
是( )
A.80° B.50° C.40° D.30°
C
B
D
4、在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标分别是A(a,b),B(4,-2),C(-a,-b),则关于点D的说法正确的是( )
甲:点D在第一象限.
乙:点D与点A关于原点对称.
丙:点D的坐标是(-4,2).
丁:点D与原点距离是2 .
A.甲乙 B.丙丁 C.甲丁 D.乙丙
B
5、 已知:如图,在 ABCD 中,E,F分别是BC,AD上的点,且BE=DF.求证AE=CF.
解:
在 ABCD中,AB=CD,
∠B=∠D,
在△ABE和△CDF中,
所以△ABE≌△CDF,所以AE=CF.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
