1.2 直角三角形(第2课时) 教学课件 --北师大版初中数学八年级(下)
文档属性
| 名称 | 1.2 直角三角形(第2课时) 教学课件 --北师大版初中数学八年级(下) |  | |
| 格式 | ppt | ||
| 文件大小 | 900.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:00 | ||
图片预览




文档简介
(共19张PPT)
第 一章 三角形的证明
第一章 三角形的证明
1.会证明直角三角形全等的判定定理;(难点)
2.会用判定定理(HL)解决有关问题。(重点)
学习目标
1、判定一般三角形全等的条件有哪几种?
SSS、SAS、ASA 、 AAS
新课导入
知识回顾
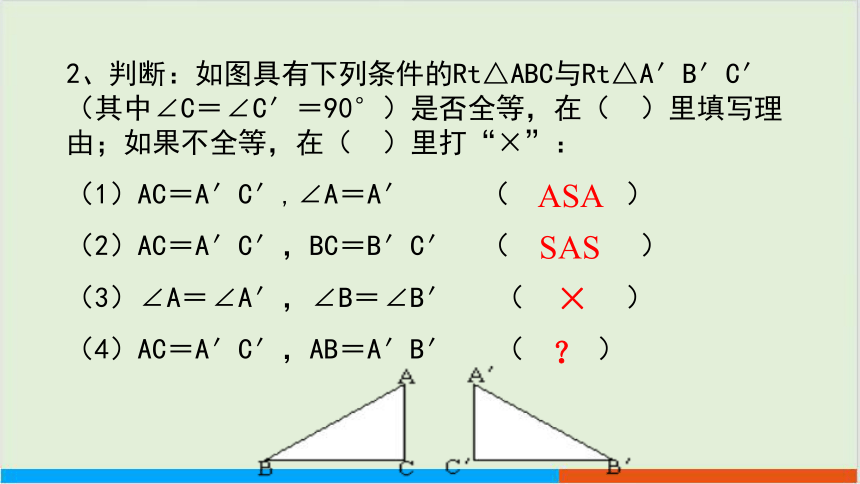
2、判断:如图具有下列条件的Rt△ABC与Rt△A′B′C′(其中∠C=∠C′=90°)是否全等,在( )里填写理由;如果不全等,在( )里打“×”:
(1)AC=A′C′,∠A=A′ ( )
(2)AC=A′C′,BC=B′C′ ( )
(3)∠A=∠A′,∠B=∠B′ ( )
(4)AC=A′C′,AB=A′B′ ( )
ASA
SAS
×
?
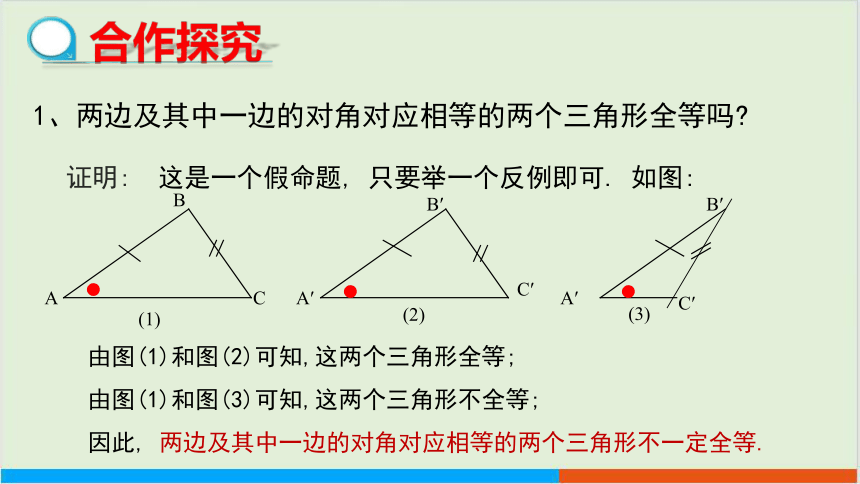
1、两边及其中一边的对角对应相等的两个三角形全等吗
证明: 这是一个假命题, 只要举一个反例即可. 如图:
A
B
C
A′
B′
C′
A′
B′
C′
●
●
●
(1)
(2)
(3)
由图(1)和图(2)可知,这两个三角形全等;
由图(1)和图(3)可知,这两个三角形不全等;
因此, 两边及其中一边的对角对应相等的两个三角形不一定全等.
合作探究
做一做:已知一条直角边和斜边,求作一个直角三角形.
已知:如图,线段a=4cm,c=5cm(a求作:Rt △ABC,使∠C= ∠ α ,BC=a,AB=c.
2、如果其中一组等边的所对的角是直角, 那么这两个三角形全等吗?.
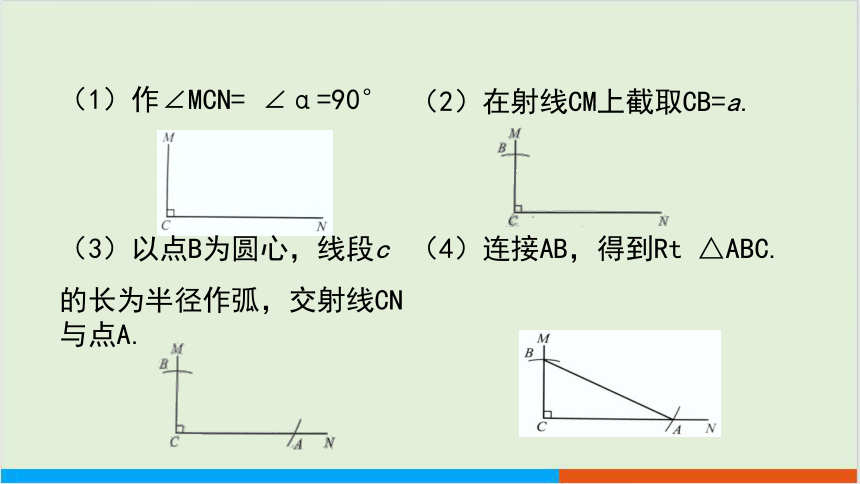
(1)作∠MCN= ∠α=90°
(2)在射线CM上截取CB=a.
(3)以点B为圆心,线段c
的长为半径作弧,交射线CN与点A.
(4)连接AB,得到Rt △ABC.
3、观察对比同桌作出的三角形是否全等?
4、把你们所作的三角形剪下来重叠在一起看是否重合?
1、在上面的做一做中,如果分别取其他长度,且满足(a2、由此你是否能发现判定直角三角形全等的一种“特有”方法?
请尝试用规范数学语言概括你的发现。
(学生通过小组讨论或交流)
得出定理:
3、如何证明它的正确性呢?
知识讲解
证明:在△ABC中,
∵∠C=90°,
∴BC2=AB2-AC2(勾股定理).
同理,B′C′2=A′B′2-A′C′2 .
∵AB=A′B′,AC=A′C′,
∴BC=B′C′.
∴ △ABC ≌ △A′B′C′(SSS).
已知:如图, 在△ABC和△A′B′C′中, ∠C=∠C′=90°, AC=A′C ′, AB=A′B′ 求证:△ABC≌△A′B′C′ .
A
B
C
A′
B′
C′
斜边和一条直角边对应相等的两个直角三角形全等
简述为:“斜边、直角边”或“HL”
几何语言:
在△ABC和△A′B′C′中, ∠C=∠C′=900
∵ BC=B′C ′, AB=A′B′
∴ Rt△ABC≌Rt△A′B′C′.(HL)
A
B
C
A′
B′
C′
例 如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角 ∠B和∠F的大小有什么关系?
解:根据题意,可知∠BAC= ∠EDF=90°,
∴Rt △BAC ≌Rt △EDF(HL)
∴ ∠B= ∠DEF(全等三角形的对应角相等)
∵ ∠DEF+ ∠F=90°(直角三角形的两锐角互余)
∴ ∠B+ ∠F=90°.
1. 判断下列命题的真假,并说明理由:
两个锐角对应相等的两个直角三角形全等;
斜边及一个锐角对应相等的两个直角三角形全等;
两直角边对应相等的两个直角三角形全等;
一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.
假
真
真
真
跟踪训练
2、如图,两根长度为12m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗?说明理由。
解:相等。
根据题意可知,∠AOC=∠AOB=90°,
AB=AC,AO=AO
∴Rt△AOB≌Rt△AOC (HL)
∴ OB=OC (全等三角形对应边相等)
直角三角形全等的判定
一般三角形全等的判定
“SAS”
“ ASA ”
“ AAS ”
“ SSS ”
“ SAS ”
“ ASA ”
“ AAS ”
“ HL ”
灵活运用各种方法证明直角三角形全等
“ SSS ”
课堂小结
1、已知:如图,D是△ABC的BC边的中点,DE⊥AC,DF⊥AB,垂足分别是E.F,且DE=DF,求证:△ABC是等腰三角形.
证明:∵ D是△ABC的BC边的中点,
∴BD=CD.
∵ DE⊥AC,DF⊥AB,
∴∠1=∠2=90°.
∵BD=CD,DE=DF,
∴Rt△BDF≌Rt△CDE (HL),
∴∠B=∠C,∴△ABC是等腰三角形.
1
2
当堂检测
2、已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为EF,且DE=BF,求证:(1)AE=CF;(2)AB∥CD.
证明:(1)∵ DE⊥AC,BF⊥AC,
∴∠1=∠2=90°.
∵AB=CD,DE=BF,
∴Rt△ABF≌Rt△CDE (HL) ,∴AF=CE,
∴AF-EF=CE-EF,即AE=CF.
(2) ∵Rt△ABF≌Rt△CDE (HL),
∴∠A=∠C, ∴AB∥CD(内错角相等,两直线平行)
1
2
3.如图, 已知∠ACB=∠BDA=90°, 要使△ABC≌△BDA, 还需要什么条件 把它们分别写出来.
增加AC=BD;
A
B
C
D
增加BC=AD;
增加∠ABC=∠BAD ;
增加∠CAB=∠DBA ;
你能分别写出它们的证明过程吗
若AD,BC相交于点O,图中还有全等的三角形吗
O
第 一章 三角形的证明
第一章 三角形的证明
1.会证明直角三角形全等的判定定理;(难点)
2.会用判定定理(HL)解决有关问题。(重点)
学习目标
1、判定一般三角形全等的条件有哪几种?
SSS、SAS、ASA 、 AAS
新课导入
知识回顾
2、判断:如图具有下列条件的Rt△ABC与Rt△A′B′C′(其中∠C=∠C′=90°)是否全等,在( )里填写理由;如果不全等,在( )里打“×”:
(1)AC=A′C′,∠A=A′ ( )
(2)AC=A′C′,BC=B′C′ ( )
(3)∠A=∠A′,∠B=∠B′ ( )
(4)AC=A′C′,AB=A′B′ ( )
ASA
SAS
×
?
1、两边及其中一边的对角对应相等的两个三角形全等吗
证明: 这是一个假命题, 只要举一个反例即可. 如图:
A
B
C
A′
B′
C′
A′
B′
C′
●
●
●
(1)
(2)
(3)
由图(1)和图(2)可知,这两个三角形全等;
由图(1)和图(3)可知,这两个三角形不全等;
因此, 两边及其中一边的对角对应相等的两个三角形不一定全等.
合作探究
做一做:已知一条直角边和斜边,求作一个直角三角形.
已知:如图,线段a=4cm,c=5cm(a
2、如果其中一组等边的所对的角是直角, 那么这两个三角形全等吗?.
(1)作∠MCN= ∠α=90°
(2)在射线CM上截取CB=a.
(3)以点B为圆心,线段c
的长为半径作弧,交射线CN与点A.
(4)连接AB,得到Rt △ABC.
3、观察对比同桌作出的三角形是否全等?
4、把你们所作的三角形剪下来重叠在一起看是否重合?
1、在上面的做一做中,如果分别取其他长度,且满足(a
请尝试用规范数学语言概括你的发现。
(学生通过小组讨论或交流)
得出定理:
3、如何证明它的正确性呢?
知识讲解
证明:在△ABC中,
∵∠C=90°,
∴BC2=AB2-AC2(勾股定理).
同理,B′C′2=A′B′2-A′C′2 .
∵AB=A′B′,AC=A′C′,
∴BC=B′C′.
∴ △ABC ≌ △A′B′C′(SSS).
已知:如图, 在△ABC和△A′B′C′中, ∠C=∠C′=90°, AC=A′C ′, AB=A′B′ 求证:△ABC≌△A′B′C′ .
A
B
C
A′
B′
C′
斜边和一条直角边对应相等的两个直角三角形全等
简述为:“斜边、直角边”或“HL”
几何语言:
在△ABC和△A′B′C′中, ∠C=∠C′=900
∵ BC=B′C ′, AB=A′B′
∴ Rt△ABC≌Rt△A′B′C′.(HL)
A
B
C
A′
B′
C′
例 如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角 ∠B和∠F的大小有什么关系?
解:根据题意,可知∠BAC= ∠EDF=90°,
∴Rt △BAC ≌Rt △EDF(HL)
∴ ∠B= ∠DEF(全等三角形的对应角相等)
∵ ∠DEF+ ∠F=90°(直角三角形的两锐角互余)
∴ ∠B+ ∠F=90°.
1. 判断下列命题的真假,并说明理由:
两个锐角对应相等的两个直角三角形全等;
斜边及一个锐角对应相等的两个直角三角形全等;
两直角边对应相等的两个直角三角形全等;
一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.
假
真
真
真
跟踪训练
2、如图,两根长度为12m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗?说明理由。
解:相等。
根据题意可知,∠AOC=∠AOB=90°,
AB=AC,AO=AO
∴Rt△AOB≌Rt△AOC (HL)
∴ OB=OC (全等三角形对应边相等)
直角三角形全等的判定
一般三角形全等的判定
“SAS”
“ ASA ”
“ AAS ”
“ SSS ”
“ SAS ”
“ ASA ”
“ AAS ”
“ HL ”
灵活运用各种方法证明直角三角形全等
“ SSS ”
课堂小结
1、已知:如图,D是△ABC的BC边的中点,DE⊥AC,DF⊥AB,垂足分别是E.F,且DE=DF,求证:△ABC是等腰三角形.
证明:∵ D是△ABC的BC边的中点,
∴BD=CD.
∵ DE⊥AC,DF⊥AB,
∴∠1=∠2=90°.
∵BD=CD,DE=DF,
∴Rt△BDF≌Rt△CDE (HL),
∴∠B=∠C,∴△ABC是等腰三角形.
1
2
当堂检测
2、已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为EF,且DE=BF,求证:(1)AE=CF;(2)AB∥CD.
证明:(1)∵ DE⊥AC,BF⊥AC,
∴∠1=∠2=90°.
∵AB=CD,DE=BF,
∴Rt△ABF≌Rt△CDE (HL) ,∴AF=CE,
∴AF-EF=CE-EF,即AE=CF.
(2) ∵Rt△ABF≌Rt△CDE (HL),
∴∠A=∠C, ∴AB∥CD(内错角相等,两直线平行)
1
2
3.如图, 已知∠ACB=∠BDA=90°, 要使△ABC≌△BDA, 还需要什么条件 把它们分别写出来.
增加AC=BD;
A
B
C
D
增加BC=AD;
增加∠ABC=∠BAD ;
增加∠CAB=∠DBA ;
你能分别写出它们的证明过程吗
若AD,BC相交于点O,图中还有全等的三角形吗
O
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
