1.3 线段的垂直平分线(第2课时) 教学课件 --北师大版初中数学八年级(下)
文档属性
| 名称 | 1.3 线段的垂直平分线(第2课时) 教学课件 --北师大版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 396.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:00 | ||
图片预览





文档简介
(共16张PPT)
第一章 三角形的证明
1.3线段的垂直平分线(第2课时)
第一章 三角形的证明
学习目标
1.掌握和证明三角形的三条边的垂直平分线的性质定理。(重点)
2.已知底边和底边上的高,能用尺规作等腰三角形。(难点)
已知:线段AB,(如图).
求作:线段AB的垂直平分线.
用尺规作线段的垂直平分线.
1.分别以点A和B为圆心,以大于
长为半径作弧,两弧交于点C和D.
A
B
C
D
2.作直线CD.
则直线CD就是线段AB的垂直平分线.
.
.
作法:
知识回顾
例2 求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
已知:如图,在△ABC中,边AB的垂直平分线与边BC的垂直平分线相交于点P.
求证:边AC的垂直平分线经过点P,且PA=PB=PC.
A
B
C
P
证明:∵点P在线段AB的垂直平分线上,
∴PA=PB(线段垂直平分线上 的点到这条
线段两个端点的距离相等)
同理,PB=PC.
∴PA=PB=PC
∴点P在线段AC的垂直平分线上
(到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上),
即 边AC的垂直平分线经过点P.
知识讲解
A
B
C
P
a
b
c
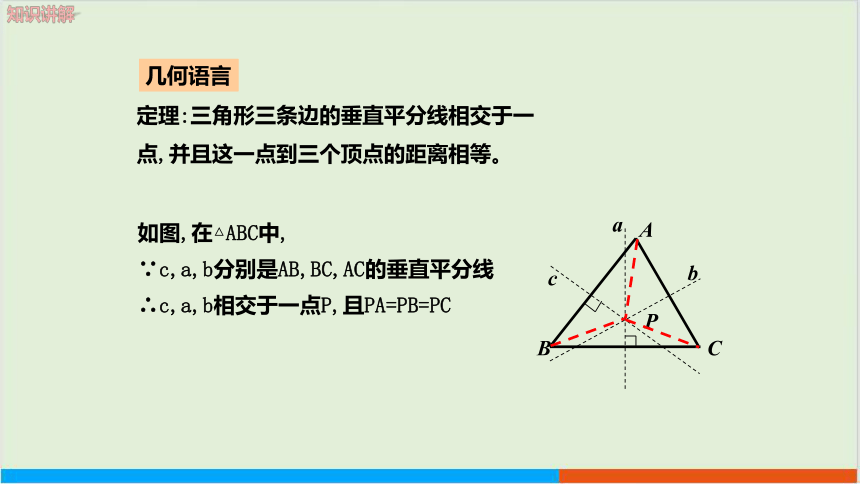
定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
如图,在△ABC中,
∵c,a,b分别是AB,BC,AC的垂直平分线∴c,a,b相交于一点P,且PA=PB=PC
几何语言
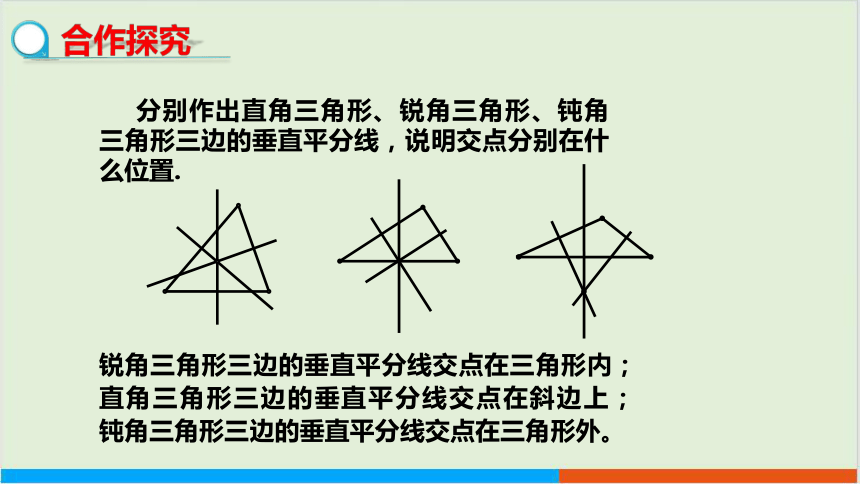
分别作出直角三角形、锐角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
合作探究
锐角三角形三边的垂直平分线交点在三角形内;直角三角形三边的垂直平分线交点在斜边上;
钝角三角形三边的垂直平分线交点在三角形外。
1.已知三角形的一条边及这条边上的高,你能作出三角形吗 如果能,能作几个 所作出的三角形都全等吗
2.已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
3.已知底边及底边上的高,用尺规作等腰三角形.
例3 已知一个等腰三角形的底边和底边上的高,求作这个等腰三角形。
h
a
已知:线段a、h
求作:△ABC,使AB=AC,且BC=a,
高AD=h。
例题讲解
已知:线段a、h。
求作:△ABC,使AB=AC,且BC=a,
高AD=h。
作法:
N
M
C
B
h
a
A
D
1.作线段BC=a;
2.作线段BC的垂直平分线MN交BC于D点;
3.在直线MN上作线段DA,使DA=h;
4.连接AB、AC.
△ABC为所求的等腰三角形。
P
●
m
做一做
已知直线l和l上一点P,利用尺规作l的垂线,使它经过点P。
如果点P在直线外呢?交流一下。
议一议
合作探究
1.已知三角形的一条边及这条边上的高,能作出_____个三角形, 所作出的三角形___都全等.
2.已知等腰三角形的底及底边上的高,能用尺规作出等腰三角形____个
无数
不
两
当堂检测
3.已知线段a,求作以a为底,以 a为高的等腰三角形。这个等腰三角形有什么特征
4.已知:在△ABC中,ON是AB的垂直平分线,OA=OC
求证:点O在BC的垂直平分线上.
5.如图,AC=AD,BC=BD,则( )
A.CD垂直平分AD B.AB垂直平分CD
C.CD平分∠ACB D.以上结论均不对
6.如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
B
C
8.①线段垂直平分线上任一点到线段两端距离相等;②线段上任一点到垂直平分线两端距离相等;③经过线段中点的直线只有一条;④点P在线段AB外且PA=PB,过P作直线MN,则MN是线段AB的垂直平分线;⑤过线段上任一点可以作这条线段的中垂线.正确的有( )
A.1个 B.2个 C.3个 D.4个
7.底边AB=a的等腰三角形有_________个,符合条件的顶点C在线段AB的______________上.
9.在△ABC中,AB=AC,AB的垂直平分线与边AC所在的直线相交所成锐角为50°,△ABC的底角∠B的大小为___________
无数
垂直平分线
A
20°或70°
1.定理:
三角形三条边的垂直平分线____________________,
并且这一点到__________________的距离相等.
相交于一点
三个顶点
2.锐角三角形三边的垂直平分线交点在三角形内; 直角三角形三边的垂直平分线交点在斜边上;
钝角三角形三边的垂直平分线交点在三角形外。
课堂小结
第一章 三角形的证明
1.3线段的垂直平分线(第2课时)
第一章 三角形的证明
学习目标
1.掌握和证明三角形的三条边的垂直平分线的性质定理。(重点)
2.已知底边和底边上的高,能用尺规作等腰三角形。(难点)
已知:线段AB,(如图).
求作:线段AB的垂直平分线.
用尺规作线段的垂直平分线.
1.分别以点A和B为圆心,以大于
长为半径作弧,两弧交于点C和D.
A
B
C
D
2.作直线CD.
则直线CD就是线段AB的垂直平分线.
.
.
作法:
知识回顾
例2 求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
已知:如图,在△ABC中,边AB的垂直平分线与边BC的垂直平分线相交于点P.
求证:边AC的垂直平分线经过点P,且PA=PB=PC.
A
B
C
P
证明:∵点P在线段AB的垂直平分线上,
∴PA=PB(线段垂直平分线上 的点到这条
线段两个端点的距离相等)
同理,PB=PC.
∴PA=PB=PC
∴点P在线段AC的垂直平分线上
(到一条线段两个端点距离相等的点,
在这条线段的垂直平分线上),
即 边AC的垂直平分线经过点P.
知识讲解
A
B
C
P
a
b
c
定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
如图,在△ABC中,
∵c,a,b分别是AB,BC,AC的垂直平分线∴c,a,b相交于一点P,且PA=PB=PC
几何语言
分别作出直角三角形、锐角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
合作探究
锐角三角形三边的垂直平分线交点在三角形内;直角三角形三边的垂直平分线交点在斜边上;
钝角三角形三边的垂直平分线交点在三角形外。
1.已知三角形的一条边及这条边上的高,你能作出三角形吗 如果能,能作几个 所作出的三角形都全等吗
2.已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
3.已知底边及底边上的高,用尺规作等腰三角形.
例3 已知一个等腰三角形的底边和底边上的高,求作这个等腰三角形。
h
a
已知:线段a、h
求作:△ABC,使AB=AC,且BC=a,
高AD=h。
例题讲解
已知:线段a、h。
求作:△ABC,使AB=AC,且BC=a,
高AD=h。
作法:
N
M
C
B
h
a
A
D
1.作线段BC=a;
2.作线段BC的垂直平分线MN交BC于D点;
3.在直线MN上作线段DA,使DA=h;
4.连接AB、AC.
△ABC为所求的等腰三角形。
P
●
m
做一做
已知直线l和l上一点P,利用尺规作l的垂线,使它经过点P。
如果点P在直线外呢?交流一下。
议一议
合作探究
1.已知三角形的一条边及这条边上的高,能作出_____个三角形, 所作出的三角形___都全等.
2.已知等腰三角形的底及底边上的高,能用尺规作出等腰三角形____个
无数
不
两
当堂检测
3.已知线段a,求作以a为底,以 a为高的等腰三角形。这个等腰三角形有什么特征
4.已知:在△ABC中,ON是AB的垂直平分线,OA=OC
求证:点O在BC的垂直平分线上.
5.如图,AC=AD,BC=BD,则( )
A.CD垂直平分AD B.AB垂直平分CD
C.CD平分∠ACB D.以上结论均不对
6.如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
B
C
8.①线段垂直平分线上任一点到线段两端距离相等;②线段上任一点到垂直平分线两端距离相等;③经过线段中点的直线只有一条;④点P在线段AB外且PA=PB,过P作直线MN,则MN是线段AB的垂直平分线;⑤过线段上任一点可以作这条线段的中垂线.正确的有( )
A.1个 B.2个 C.3个 D.4个
7.底边AB=a的等腰三角形有_________个,符合条件的顶点C在线段AB的______________上.
9.在△ABC中,AB=AC,AB的垂直平分线与边AC所在的直线相交所成锐角为50°,△ABC的底角∠B的大小为___________
无数
垂直平分线
A
20°或70°
1.定理:
三角形三条边的垂直平分线____________________,
并且这一点到__________________的距离相等.
相交于一点
三个顶点
2.锐角三角形三边的垂直平分线交点在三角形内; 直角三角形三边的垂直平分线交点在斜边上;
钝角三角形三边的垂直平分线交点在三角形外。
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
