1.4 角平分线(第1课时) 教学课件 --北师大版初中数学八年级(下)
文档属性
| 名称 | 1.4 角平分线(第1课时) 教学课件 --北师大版初中数学八年级(下) |

|
|
| 格式 | ppt | ||
| 文件大小 | 877.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:00 | ||
图片预览




文档简介
(共20张PPT)
第一章 三角形的证明
第一章 三角形的证明
学习目标
1、会证明角平分线的性质定理及逆定理;(重点)
2、会运用角平分线的性质定理及逆定理解决有关的数学问题.(难点)
你能利用尺规作出角平分线吗
你还记得角平分线上的点有什么性质吗
角平分线上的点到这个角的两边距离相等
怎么证明这一结论。
复习导入
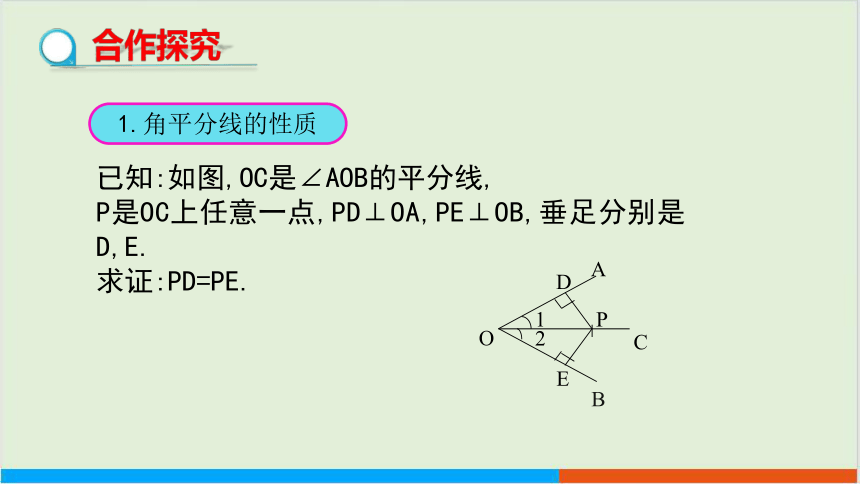
已知:如图,OC是∠AOB的平分线,
P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E.
求证:PD=PE.
O
C
B
1
A
2
P
D
E
合作探究
1.角平分线的性质
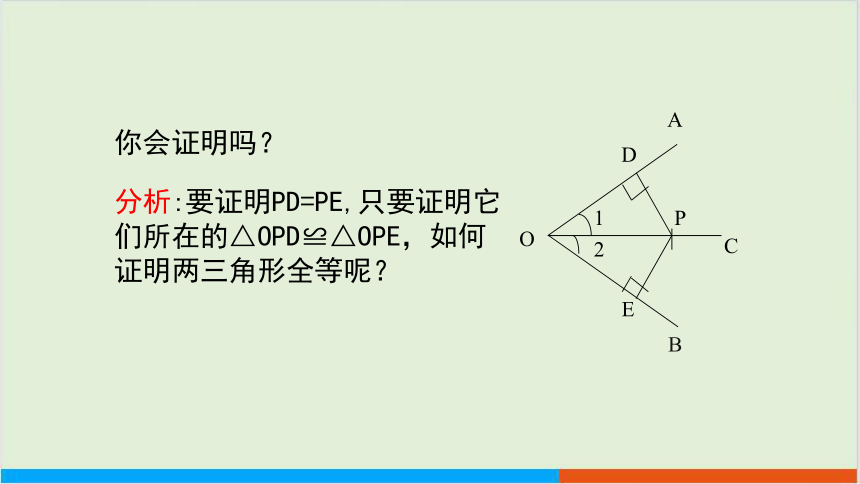
你会证明吗?
分析:要证明PD=PE,只要证明它们所在的△OPD≌△OPE,如何证明两三角形全等呢?
O
C
B
1
A
2
P
D
E
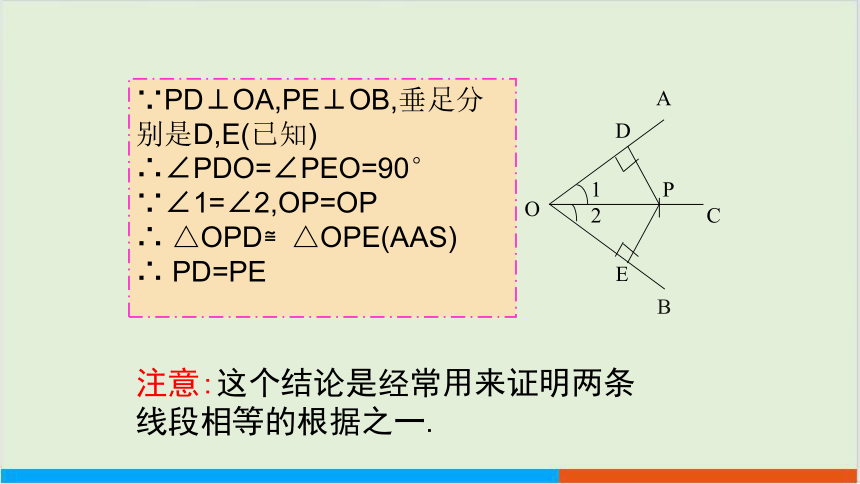
注意:这个结论是经常用来证明两条线段相等的根据之一.
O
C
B
1
A
2
P
D
E
∵PD⊥OA,PE⊥OB,垂足分别是D,E(已知)
∴∠PDO=∠PEO=90°
∵∠1=∠2,OP=OP
∴ △OPD≌△OPE(AAS)
∴ PD=PE
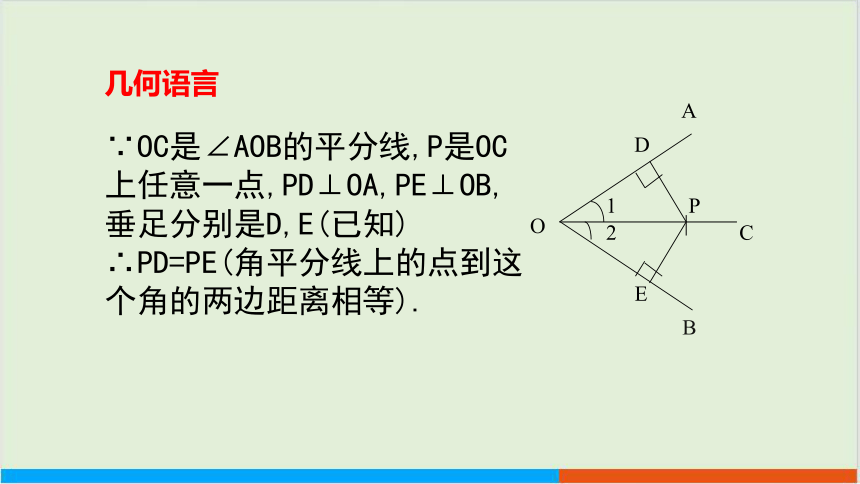
∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,
垂足分别是D,E(已知)
∴PD=PE(角平分线上的点到这个角的两边距离相等).
O
C
B
1
A
2
P
D
E
几何语言
你能写出“定理 角平分线上的点到这个角的两边距离相等”的逆命题吗
逆命题
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
它是真命题吗
如果是.请你证明它.
2.角平分线的判定
合作探究
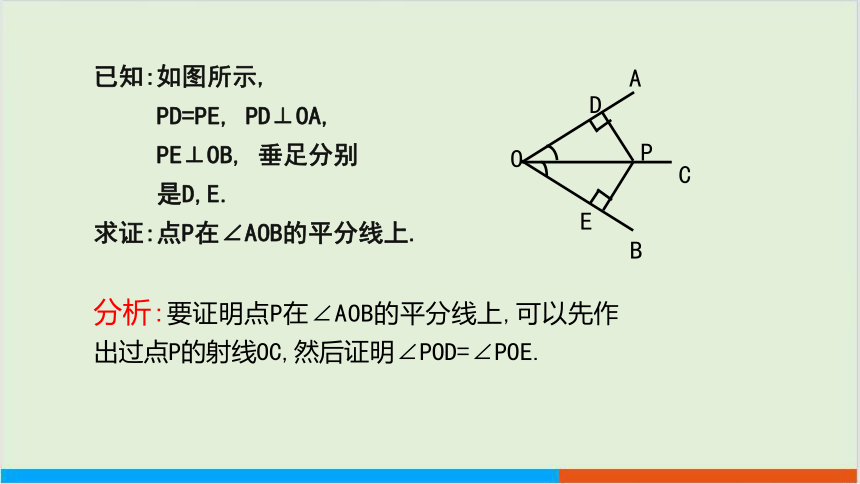
已知:如图所示,
PD=PE, PD⊥OA,
PE⊥OB, 垂足分别
是D,E.
求证:点P在∠AOB的平分线上.
分析:要证明点P在∠AOB的平分线上,可以先作出过点P的射线OC,然后证明∠POD=∠POE.
B
A
C
D
E
O
P
证明:∵PD⊥OA,PE⊥OB
∴△POD和△POE都是直角三角形
∵PD=PE,OP=OP
∴Rt△POD≌Rt△POE(HL)
∴ ∠POD=∠POE
∴ OC是∠AOB的平分线
逆定理 在一个角的内部,且到角的两边距离 相等的点,在这个角的平分线上.
如图,
∵PD=PE, PD⊥OA,PE⊥OB,垂足分别是D,E(已知),
∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).
老师提示:这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.
C
B
1
A
2
P
D
E
O
例1. 如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求DE的长.
例题讲解
已知:如图,点P是∠AOB 内的一点,PD⊥OA,PE⊥OB,垂足分别是D,E.且PD=PE,
求证:OP平分∠AOB.
O
C
B
1
A
2
P
D
E
合作探究
1.如图,AD,AE分别是△ABC中∠A的内角平分线外角平分线,它们有什么关系
你能说出结论并能证明它吗?
E
D
A
B
C
F
跟踪训练
2.如图,一目标在A区,到公路,铁路距离相等,离公路与铁路的交叉处500m.在图上标出它的位置(比例尺 1:20 000).
A区
1.角平分线性质定理
2.符号表示
∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E ∴PD=PE
3.逆定理
4.符号表示∵PD=PE,PD⊥OA,PE⊥OB,垂足分别是D,E(已知),
∴点P在∠AOB的平分线上.
O
C
B
1
A
2
P
D
E
课堂小结
1.角平分线上的点到______________距离相等;
到一个角的两边距离相等的点都在_____________.
这个角的两边
这个角的平分线上
2.如图,∠AOB=60°,PD⊥OA于D,
PE⊥OB于E,且PD=PE,则∠1=_________.
30°
当堂检测
3. 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等.
C●
D●
A
B
O
4.已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
B
A
E
D
C
F
第一章 三角形的证明
第一章 三角形的证明
学习目标
1、会证明角平分线的性质定理及逆定理;(重点)
2、会运用角平分线的性质定理及逆定理解决有关的数学问题.(难点)
你能利用尺规作出角平分线吗
你还记得角平分线上的点有什么性质吗
角平分线上的点到这个角的两边距离相等
怎么证明这一结论。
复习导入
已知:如图,OC是∠AOB的平分线,
P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E.
求证:PD=PE.
O
C
B
1
A
2
P
D
E
合作探究
1.角平分线的性质
你会证明吗?
分析:要证明PD=PE,只要证明它们所在的△OPD≌△OPE,如何证明两三角形全等呢?
O
C
B
1
A
2
P
D
E
注意:这个结论是经常用来证明两条线段相等的根据之一.
O
C
B
1
A
2
P
D
E
∵PD⊥OA,PE⊥OB,垂足分别是D,E(已知)
∴∠PDO=∠PEO=90°
∵∠1=∠2,OP=OP
∴ △OPD≌△OPE(AAS)
∴ PD=PE
∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,
垂足分别是D,E(已知)
∴PD=PE(角平分线上的点到这个角的两边距离相等).
O
C
B
1
A
2
P
D
E
几何语言
你能写出“定理 角平分线上的点到这个角的两边距离相等”的逆命题吗
逆命题
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
它是真命题吗
如果是.请你证明它.
2.角平分线的判定
合作探究
已知:如图所示,
PD=PE, PD⊥OA,
PE⊥OB, 垂足分别
是D,E.
求证:点P在∠AOB的平分线上.
分析:要证明点P在∠AOB的平分线上,可以先作出过点P的射线OC,然后证明∠POD=∠POE.
B
A
C
D
E
O
P
证明:∵PD⊥OA,PE⊥OB
∴△POD和△POE都是直角三角形
∵PD=PE,OP=OP
∴Rt△POD≌Rt△POE(HL)
∴ ∠POD=∠POE
∴ OC是∠AOB的平分线
逆定理 在一个角的内部,且到角的两边距离 相等的点,在这个角的平分线上.
如图,
∵PD=PE, PD⊥OA,PE⊥OB,垂足分别是D,E(已知),
∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).
老师提示:这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.
C
B
1
A
2
P
D
E
O
例1. 如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求DE的长.
例题讲解
已知:如图,点P是∠AOB 内的一点,PD⊥OA,PE⊥OB,垂足分别是D,E.且PD=PE,
求证:OP平分∠AOB.
O
C
B
1
A
2
P
D
E
合作探究
1.如图,AD,AE分别是△ABC中∠A的内角平分线外角平分线,它们有什么关系
你能说出结论并能证明它吗?
E
D
A
B
C
F
跟踪训练
2.如图,一目标在A区,到公路,铁路距离相等,离公路与铁路的交叉处500m.在图上标出它的位置(比例尺 1:20 000).
A区
1.角平分线性质定理
2.符号表示
∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E ∴PD=PE
3.逆定理
4.符号表示∵PD=PE,PD⊥OA,PE⊥OB,垂足分别是D,E(已知),
∴点P在∠AOB的平分线上.
O
C
B
1
A
2
P
D
E
课堂小结
1.角平分线上的点到______________距离相等;
到一个角的两边距离相等的点都在_____________.
这个角的两边
这个角的平分线上
2.如图,∠AOB=60°,PD⊥OA于D,
PE⊥OB于E,且PD=PE,则∠1=_________.
30°
当堂检测
3. 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等.
C●
D●
A
B
O
4.已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
B
A
E
D
C
F
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
