2.1 不等关系 教学课件 --北师大版初中数学八年级(下)
文档属性
| 名称 | 2.1 不等关系 教学课件 --北师大版初中数学八年级(下) |

|
|
| 格式 | ppt | ||
| 文件大小 | 818.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:00 | ||
图片预览





文档简介
(共20张PPT)
第二章 一元一次不等式与一元一次不等式组
第二章 一元一次不等式
与一元一次不等式组
1.理解不等式的意义;(重点)
2.能根据条件列出不等式;(难点)
3.能用实际生活背景和数学背景解释简单不等式的意义。
学习目标
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,并把它们用到了生活实践当中.
情景导入
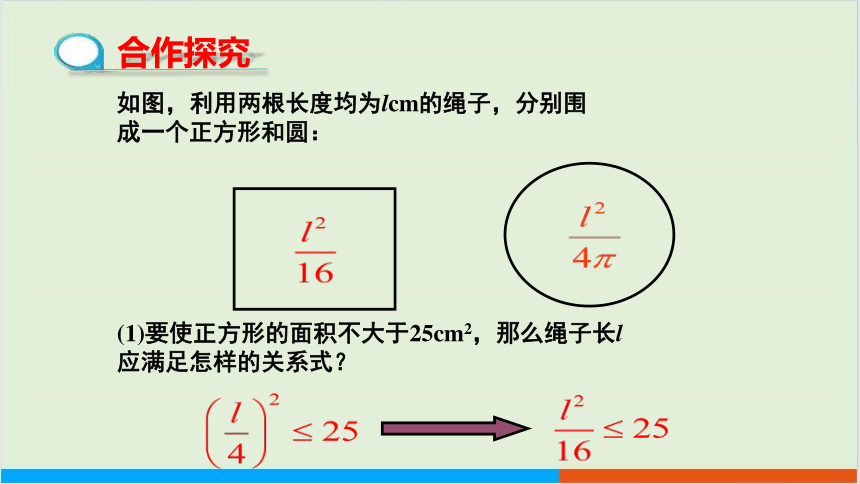
如图,利用两根长度均为lcm的绳子,分别围
成一个正方形和圆:
(1)要使正方形的面积不大于25cm2,那么绳子长l
应满足怎样的关系式?
合作探究
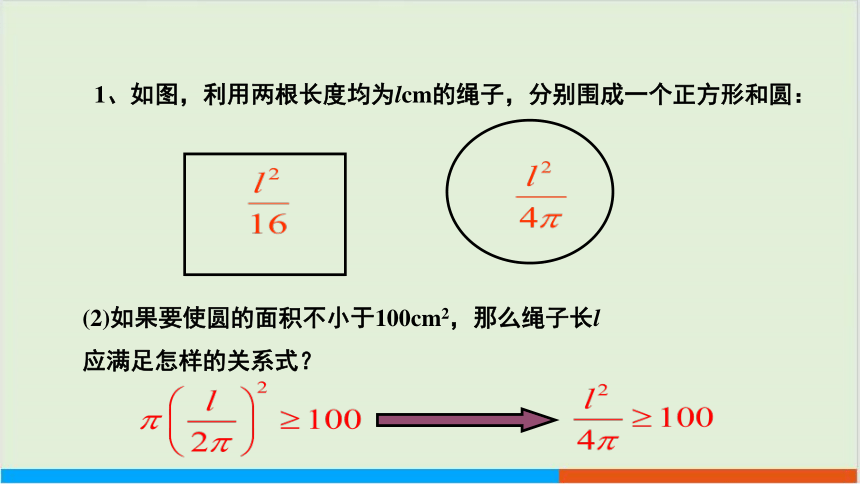
1、如图,利用两根长度均为lcm的绳子,分别围成一个正方形和圆:
(2)如果要使圆的面积不小于100cm2,那么绳子长l
应满足怎样的关系式?
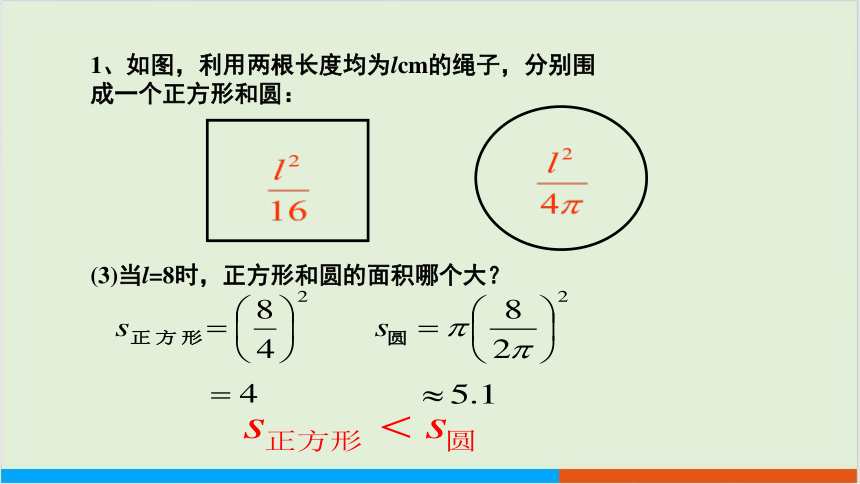
1、如图,利用两根长度均为lcm的绳子,分别围
成一个正方形和圆:
(3)当l=8时,正方形和圆的面积哪个大?
1、如图,利用两根长度均为lcm的绳子,分别围
成一个正方形和圆:
(4)当l=12时,正方形和圆的面积哪个大?
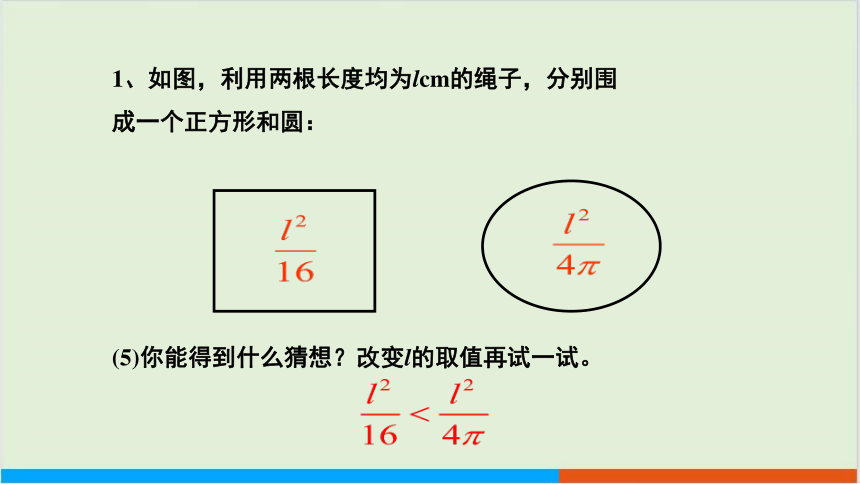
1、如图,利用两根长度均为lcm的绳子,分别围
成一个正方形和圆:
(5)你能得到什么猜想?改变l的取值再试一试。
2、通过测量一棵树的树围(树干的周长)可以计算它的树龄。通常以树干离地面1.5m的地方作为测量部位。某棵树栽种时的树围为6cm,以后10年内每年约增加3cm,这棵树至少生长多少年其树围才能超过30 cm?(只列关系式)
解:设这棵树至少生长x年其
树围才能超过30 cm,
根据题意,得
合作探究
1、观察下列关系式,你有什么发现?
由不等号连接而成
知识讲解
不等式的定义:
一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式。
知识讲解
例1、用适当的符号表示下列关系:
(1)x的3倍与8的和比x的5倍小;
(2)x2是非负数;
(3)地球上海洋的面积大于陆地面积;
(4)老师的年龄不超过学生的年龄的2倍。
解:
例题讲解
例2、请你设计不同的实际背景来表示下列不等式:
(1) (2)
“≥、≤”的意义:
(1)“≥”:a不小于(不低过)b表示为a≥b ,
a为非负数表示为a≥0 ;
(2)“≤”:a不大于(不高过)b表示为a≤b ,
a为非正数表示为a≤0 。
知识讲解
例3、甲、乙两种原料配制成某种饮料,已知这两
种原料的维生素C含量及购买这两种原料的价格如下表:
甲种原料 乙种原料
维生素C/(单位/千克) 600 100
原料价格/(元/千克) 8 4
现配制这种饮料10千克,要求至少含有4200单位
的维生素C,试写出所需甲种原料的质量x(千克)
应满足的不等式。
原料
维生素及价格
例题讲解
1、不等式的定义:
一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式。
2、“≥、≤”的意义:
(1)“≥”:a不小于(不低过)b表示为a≥b ,
a为非负数表示为a≥0 ;
(2)“≤”:a不大于(不高过)b表示为a≤b ,
a为非正数表示为a≤0 。
课堂小结
1、用适当的符号表示下列不等式:
(1)a是非负数;
(2)直角三角形斜边c比它的两直角边a、b都长;
(3)x与17的和比它的5倍小。
当堂检测
2、从1、3、5、7、9中任取两个数就组成一组数,
写出其中两数之和小于10的所有数组。
3、在通过桥洞时,我们往往会看到如图(1)所示
的标志,这是限制车高的标志。你知道通过该桥
洞的车高x(m)的范围吗?在通过桥面时,我们往
往会看到如图(2)所示的标志,这是限制车重的标
志。你知道通过该桥面的车重y(t)的范围吗?
(1)
(2)
10t
5m
第二章 一元一次不等式与一元一次不等式组
第二章 一元一次不等式
与一元一次不等式组
1.理解不等式的意义;(重点)
2.能根据条件列出不等式;(难点)
3.能用实际生活背景和数学背景解释简单不等式的意义。
学习目标
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,并把它们用到了生活实践当中.
情景导入
如图,利用两根长度均为lcm的绳子,分别围
成一个正方形和圆:
(1)要使正方形的面积不大于25cm2,那么绳子长l
应满足怎样的关系式?
合作探究
1、如图,利用两根长度均为lcm的绳子,分别围成一个正方形和圆:
(2)如果要使圆的面积不小于100cm2,那么绳子长l
应满足怎样的关系式?
1、如图,利用两根长度均为lcm的绳子,分别围
成一个正方形和圆:
(3)当l=8时,正方形和圆的面积哪个大?
1、如图,利用两根长度均为lcm的绳子,分别围
成一个正方形和圆:
(4)当l=12时,正方形和圆的面积哪个大?
1、如图,利用两根长度均为lcm的绳子,分别围
成一个正方形和圆:
(5)你能得到什么猜想?改变l的取值再试一试。
2、通过测量一棵树的树围(树干的周长)可以计算它的树龄。通常以树干离地面1.5m的地方作为测量部位。某棵树栽种时的树围为6cm,以后10年内每年约增加3cm,这棵树至少生长多少年其树围才能超过30 cm?(只列关系式)
解:设这棵树至少生长x年其
树围才能超过30 cm,
根据题意,得
合作探究
1、观察下列关系式,你有什么发现?
由不等号连接而成
知识讲解
不等式的定义:
一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式。
知识讲解
例1、用适当的符号表示下列关系:
(1)x的3倍与8的和比x的5倍小;
(2)x2是非负数;
(3)地球上海洋的面积大于陆地面积;
(4)老师的年龄不超过学生的年龄的2倍。
解:
例题讲解
例2、请你设计不同的实际背景来表示下列不等式:
(1) (2)
“≥、≤”的意义:
(1)“≥”:a不小于(不低过)b表示为a≥b ,
a为非负数表示为a≥0 ;
(2)“≤”:a不大于(不高过)b表示为a≤b ,
a为非正数表示为a≤0 。
知识讲解
例3、甲、乙两种原料配制成某种饮料,已知这两
种原料的维生素C含量及购买这两种原料的价格如下表:
甲种原料 乙种原料
维生素C/(单位/千克) 600 100
原料价格/(元/千克) 8 4
现配制这种饮料10千克,要求至少含有4200单位
的维生素C,试写出所需甲种原料的质量x(千克)
应满足的不等式。
原料
维生素及价格
例题讲解
1、不等式的定义:
一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式。
2、“≥、≤”的意义:
(1)“≥”:a不小于(不低过)b表示为a≥b ,
a为非负数表示为a≥0 ;
(2)“≤”:a不大于(不高过)b表示为a≤b ,
a为非正数表示为a≤0 。
课堂小结
1、用适当的符号表示下列不等式:
(1)a是非负数;
(2)直角三角形斜边c比它的两直角边a、b都长;
(3)x与17的和比它的5倍小。
当堂检测
2、从1、3、5、7、9中任取两个数就组成一组数,
写出其中两数之和小于10的所有数组。
3、在通过桥洞时,我们往往会看到如图(1)所示
的标志,这是限制车高的标志。你知道通过该桥
洞的车高x(m)的范围吗?在通过桥面时,我们往
往会看到如图(2)所示的标志,这是限制车重的标
志。你知道通过该桥面的车重y(t)的范围吗?
(1)
(2)
10t
5m
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
