22.2平行四边形的判定(第1课时)教学课件--冀教版数学八年级(下)
文档属性
| 名称 | 22.2平行四边形的判定(第1课时)教学课件--冀教版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:23:49 | ||
图片预览


文档简介
(共19张PPT)
第二十二章 四边形
第二十二章 四边形
22.2 平行四边形的判定
第一课时
学 习 目 标
1、理解一组对边平行且相等的四边形是平行四边形.(重点)
2、掌握平行四边形的判定定理,能根据不同条件灵活选取适当的判定方法进行推理论证.(难点)
A
D
B
C
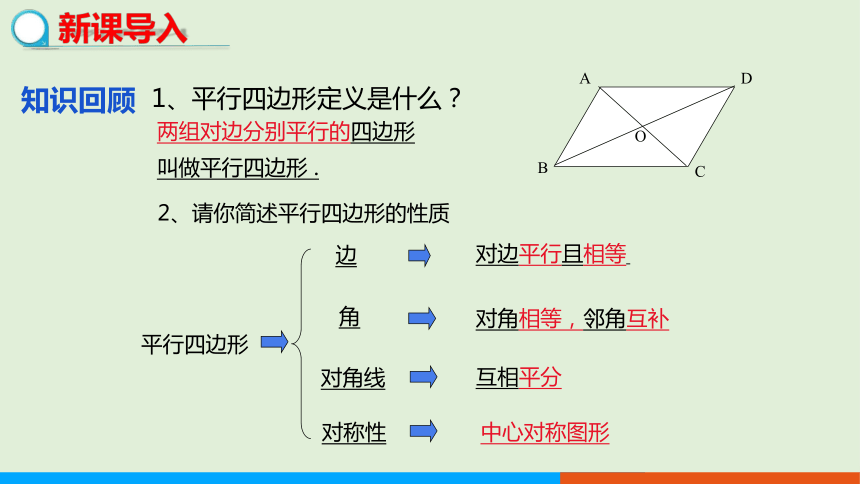
1、平行四边形定义是什么?
O
两组对边分别平行的四边形
叫做平行四边形 .
互相平分
平行四边形
边
角
对角线
对角相等,邻角互补
对称性
中心对称图形
2、请你简述平行四边形的性质
对边平行且相等
新课导入
知识回顾
怎样判定一个四边形是平行四边形?
A
D
B
C
平行四边形
边?
角?
对角线?
对称性?
思考
思考方向
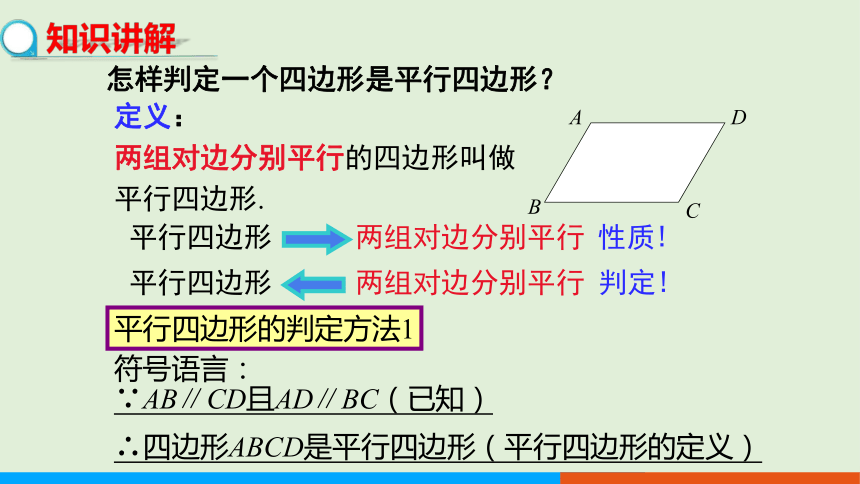
怎样判定一个四边形是平行四边形?
定义:
两组对边分别平行的四边形叫做
平行四边形.
A
D
B
C
∵AB∥CD且AD∥BC(已知)
∴四边形ABCD是平行四边形(平行四边形的定义)
符号语言:
平行四边形的判定方法1
平行四边形
两组对边分别平行
性质!
两组对边分别平行
平行四边形
判定!
知识讲解
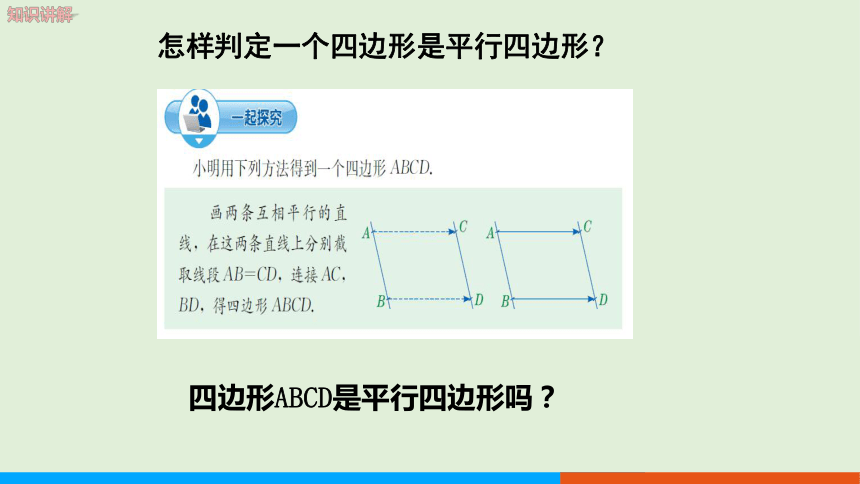
四边形ABCD是平行四边形吗?
怎样判定一个四边形是平行四边形?
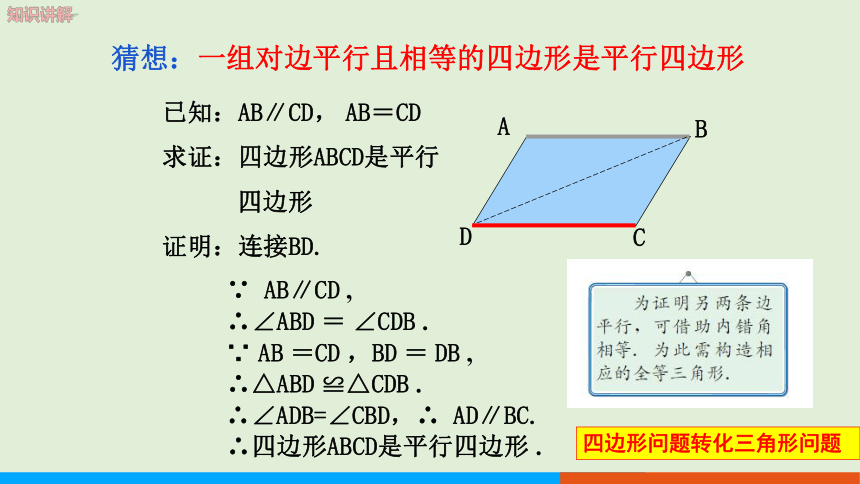
猜想:一组对边平行且相等的四边形是平行四边形
已知:AB∥CD, AB=CD
求证:四边形ABCD是平行
四边形
证明:连接BD.
A
B
C
D
∵ AB∥CD ,
∴∠ABD = ∠CDB .
∵ AB =CD ,BD = DB ,
∴△ABD ≌△CDB .
∴∠ADB=∠CBD,∴ AD∥BC.
∴四边形ABCD是平行四边形 .
四边形问题转化三角形问题
一组对边平行且相等的四边形是平行四边形.
几何语言:
∵ AD∥BC , AD=BC ,
∴ 四边形ABCD是平行四边形.
平行四边形的判定定理
A
B
C
D
条件(已知)
结论(求证)
例1 已知:如图所示,在 ABCD 中,E 为BA 延长线上一点,F 为DC 延长线上一点,且AE=CF,连接BF,DE.
求证:四边形BFDE 是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵AE=CF,
∴BE=BA+AE=DC+CF=DF,且BE∥DF.
∴四边形BFDE是平行四边形.
性质
判定
例题讲解
例2 求证:平行线间的距离处处相等
已知:如图,EF∥MN,A,B为直线EF上任意两点,AD⊥MN,垂足为D,BC⊥MN,垂足为C.
求证AD=BC.
证明:∵AD⊥MN,BC⊥MN,
∴AD∥BC.
又∵EF∥MN,
∴四边形ADCB是平行四边形.
∴AD=BC.
几何语言:
∵EF∥MN,
AD⊥MN,BC⊥MN,
∴AD=BC.
证明线段相等方法:
1. 全等三角形对应边相等。
2.平行四边形对边相等。
两组对角分别相等的四边形是平行四边形吗?
A
B
C
D
已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
一、平行四边形的判定方法
1.两组对边分别__________的四边形是平行四边形.
2.一组对边______________的四边形是平行四边形.
3.两组对角分别__________的四边形是平行四边形.
二、平行线间的距离________.
归纳总结
平行
平行且相等
相等
处处相等
1.下列条件中,能判别一个四边形是平行四边形的是( )
A.一组对边相等 B.一组对边平行
C.两条对角线相等 D.两条对角线互相平分
2.判断题:
一组对边平行,另一组对边相等的四边形是平行四边形.( )
两组对边分别平行的四边形是平行四边形.( )
两组邻角互补的四边形是平行四边形.( )
一组对边平行且相等的四边形是平行四边形.( )
两组对角分别相等的四边形是平行四边形.( )
D
随堂训练
×
√
×
√
√
3.如图,AC∥ED,点B在AC上且AB=ED=BC.找出图中的平行四边形.
A
C
B
E
D
解:四边形ABDE,BCDE都是平行四边形. 理由是:
∵ AB∥ED,AB=ED,
∴ 四边形ABDE是平行四边形.
(一组对边平行且相等的四边形平行四边形)
∵ BC∥ED, BC=ED,
∴ 四边形BCDE是平行四边形.
(一组对边平行且相等的四边形平行四边形)
平行四边形的判定
定义:两组对边分别平行的四边形是平行四边形
补充:两组对角分别相等的四边形是平行四边形
课堂小结
判定定理:一组对边平行且相等的四边形是平行四边形.
平行线间的距离处处相等
1、在□ABCD中,E、F分别为CD、AB的中点
求证:四边形EGFH是平行四边形.
证明:∵ 四边形ABCD为平行四边形,
∴四边形DEBF为平行四边形,
∴DF//EB.
∴四边形EGFH是平行四边形.
又∵E、F是CD、AB的中点,
∴AB CD 且AB=CD.
∴DE BF且DE=BF,
//
同理 AE//FC,
当堂检测
//
2、已知:平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F.
求证:四边形AECF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD且AB∥CD,∴∠1=∠2.
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFE,
∴△ABE≌△CDF(AAS).
∴AE=CF.
由AE⊥BD,CF⊥BD得:
AE ∥ CF,
∴四边形AECF是平行四边形.
第二十二章 四边形
第二十二章 四边形
22.2 平行四边形的判定
第一课时
学 习 目 标
1、理解一组对边平行且相等的四边形是平行四边形.(重点)
2、掌握平行四边形的判定定理,能根据不同条件灵活选取适当的判定方法进行推理论证.(难点)
A
D
B
C
1、平行四边形定义是什么?
O
两组对边分别平行的四边形
叫做平行四边形 .
互相平分
平行四边形
边
角
对角线
对角相等,邻角互补
对称性
中心对称图形
2、请你简述平行四边形的性质
对边平行且相等
新课导入
知识回顾
怎样判定一个四边形是平行四边形?
A
D
B
C
平行四边形
边?
角?
对角线?
对称性?
思考
思考方向
怎样判定一个四边形是平行四边形?
定义:
两组对边分别平行的四边形叫做
平行四边形.
A
D
B
C
∵AB∥CD且AD∥BC(已知)
∴四边形ABCD是平行四边形(平行四边形的定义)
符号语言:
平行四边形的判定方法1
平行四边形
两组对边分别平行
性质!
两组对边分别平行
平行四边形
判定!
知识讲解
四边形ABCD是平行四边形吗?
怎样判定一个四边形是平行四边形?
猜想:一组对边平行且相等的四边形是平行四边形
已知:AB∥CD, AB=CD
求证:四边形ABCD是平行
四边形
证明:连接BD.
A
B
C
D
∵ AB∥CD ,
∴∠ABD = ∠CDB .
∵ AB =CD ,BD = DB ,
∴△ABD ≌△CDB .
∴∠ADB=∠CBD,∴ AD∥BC.
∴四边形ABCD是平行四边形 .
四边形问题转化三角形问题
一组对边平行且相等的四边形是平行四边形.
几何语言:
∵ AD∥BC , AD=BC ,
∴ 四边形ABCD是平行四边形.
平行四边形的判定定理
A
B
C
D
条件(已知)
结论(求证)
例1 已知:如图所示,在 ABCD 中,E 为BA 延长线上一点,F 为DC 延长线上一点,且AE=CF,连接BF,DE.
求证:四边形BFDE 是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵AE=CF,
∴BE=BA+AE=DC+CF=DF,且BE∥DF.
∴四边形BFDE是平行四边形.
性质
判定
例题讲解
例2 求证:平行线间的距离处处相等
已知:如图,EF∥MN,A,B为直线EF上任意两点,AD⊥MN,垂足为D,BC⊥MN,垂足为C.
求证AD=BC.
证明:∵AD⊥MN,BC⊥MN,
∴AD∥BC.
又∵EF∥MN,
∴四边形ADCB是平行四边形.
∴AD=BC.
几何语言:
∵EF∥MN,
AD⊥MN,BC⊥MN,
∴AD=BC.
证明线段相等方法:
1. 全等三角形对应边相等。
2.平行四边形对边相等。
两组对角分别相等的四边形是平行四边形吗?
A
B
C
D
已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
一、平行四边形的判定方法
1.两组对边分别__________的四边形是平行四边形.
2.一组对边______________的四边形是平行四边形.
3.两组对角分别__________的四边形是平行四边形.
二、平行线间的距离________.
归纳总结
平行
平行且相等
相等
处处相等
1.下列条件中,能判别一个四边形是平行四边形的是( )
A.一组对边相等 B.一组对边平行
C.两条对角线相等 D.两条对角线互相平分
2.判断题:
一组对边平行,另一组对边相等的四边形是平行四边形.( )
两组对边分别平行的四边形是平行四边形.( )
两组邻角互补的四边形是平行四边形.( )
一组对边平行且相等的四边形是平行四边形.( )
两组对角分别相等的四边形是平行四边形.( )
D
随堂训练
×
√
×
√
√
3.如图,AC∥ED,点B在AC上且AB=ED=BC.找出图中的平行四边形.
A
C
B
E
D
解:四边形ABDE,BCDE都是平行四边形. 理由是:
∵ AB∥ED,AB=ED,
∴ 四边形ABDE是平行四边形.
(一组对边平行且相等的四边形平行四边形)
∵ BC∥ED, BC=ED,
∴ 四边形BCDE是平行四边形.
(一组对边平行且相等的四边形平行四边形)
平行四边形的判定
定义:两组对边分别平行的四边形是平行四边形
补充:两组对角分别相等的四边形是平行四边形
课堂小结
判定定理:一组对边平行且相等的四边形是平行四边形.
平行线间的距离处处相等
1、在□ABCD中,E、F分别为CD、AB的中点
求证:四边形EGFH是平行四边形.
证明:∵ 四边形ABCD为平行四边形,
∴四边形DEBF为平行四边形,
∴DF//EB.
∴四边形EGFH是平行四边形.
又∵E、F是CD、AB的中点,
∴AB CD 且AB=CD.
∴DE BF且DE=BF,
//
同理 AE//FC,
当堂检测
//
2、已知:平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F.
求证:四边形AECF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD且AB∥CD,∴∠1=∠2.
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFE,
∴△ABE≌△CDF(AAS).
∴AE=CF.
由AE⊥BD,CF⊥BD得:
AE ∥ CF,
∴四边形AECF是平行四边形.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
