3.1 图形的平移(第3课时) 教学课件 --北师大版初中数学八年级(下)
文档属性
| 名称 | 3.1 图形的平移(第3课时) 教学课件 --北师大版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 941.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:00 | ||
图片预览








文档简介
(共26张PPT)
第三章 图形的平移与旋转
第三章 图形的平移与旋转
3.1 图形的平移
(第3课时)
1.通过具体实例认识图形的两次平移变换,探索它的基本性质;(重点)
2.能按要求画出平面图形两次平移后的图形。(难点)
学习目标
点的平移与点的坐标变化规律:
左、右平移,横变纵不变,“右加左减”;
上、下平移,纵变横不变,“上加下减”.
知识回顾
在平面直角坐标系中,一个点沿x轴方向平移a
(a>0)个单位长度,再沿y轴方向平移b(b>0)个单位长度,得到点的坐标是什么?
知识讲解
1.两次平移的坐标变化规律
如图,将点A(-2, -3)向右平移5个单位长度,得到点A1,再向上平移6个单位,得到点A2,在图上标出这个点,并写出它的坐标.
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A1
(3, -3)
A
(-2, -3)
A2
(3, 3)
(-2, -3)
右移5个单位
(3, -3)
横坐标+5
(3, -3)
上移6个单位
(3, 3)
纵坐标+6
平移前后的坐标有什么关系
知识讲解
(1)点(x, y)向左平移a(a>0)个单位,再向上平移
b(b>0)个单位 平移后的坐标为(x-a, y+b);
(2)点(x, y)向右平移a(a>0)个单位,再向下平移
a(a>0)个单位 平移后的坐标为 (x+a, y-b);
规律
知识讲解
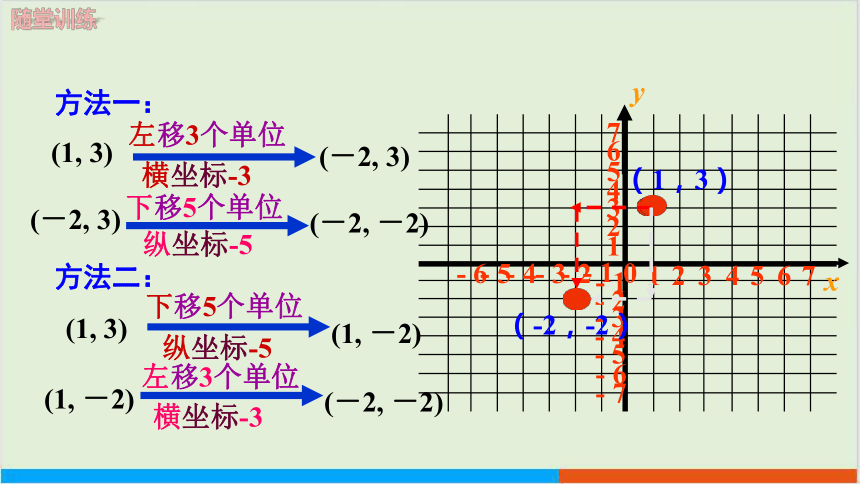
在平面直角坐标系中,有一点(1,3),要使它平移到点(-2,-2),应怎样平移?说出平移的路线.
提示:
点的斜向平移,可以通过点的左右和上下移动共同来完成
千万不要走斜线哦
随堂训练
(1, 3)
左移3个单位
(-2, 3)
横坐标-3
(-2, 3)
下移5个单位
(-2, -2)
纵坐标-5
- 5
- 4
- 3
- 2
- 6
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
x
- 5
- 4
- 3
- 2
- 7
- 6
- 1
- 1
(1,3)
(-2,-2)
y
方法一:
(1, 3)
下移5个单位
(1, -2)
纵坐标-5
(1, -2)
左移3个单位
(-2, -2)
横坐标-3
方法二:
随堂训练
一个图形依次沿 x轴方向、y轴方向平移后所得
图形与原来的图形相比, 位置有什么变化?它们对
应点的坐标之间有怎样的关系?
2.两次平移后的图形与原图形之间的平移方向、距离
知识讲解
一个图形依次沿x轴方向、y轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的.
总结
知识讲解
例2.如图,四边形ABCD各顶点的坐标分别为A(-3, 5),B(-4, 3),C (-1,1),D(-1,4),将四边形ABCD先向上平移3个单位长度, 再向右平移4个单位长度,得到四边形A′B′C′D′.
例题讲解
(1)四边形A′B′C′D′与四边形ABCD对应点的横坐标有 什么关系?纵坐标呢?分别写出点A', B', C',D'的 坐标;
(2)如果将四边形A′B′C′D′看成是由四边形ABCD经 过一次平移得到的,请指出这一平移的平移方向和平移距离.
知识讲解
(1)四边形A′B′C′D′与四边形ABCD相比,对应点的横
坐标分别增加了4, 纵坐标分别增加了3; A′(1,8),
B′(0, 6),C'(3, 4),D′(3, 7);
(2 )如图,连接AA′,由图可
知, AA′ =
因此,如果将四边形
A′B′C′D′看成是由四边形
ABCD经过一次平移得到
的,那么这一平移的平移
方向是由A到A′的方向,平移距离是5个单位长度.
解:
知识讲解
(1)在平面直角坐标系中描出点A( 6, 0),B(10, 3),
C(9, 1),D(12, 0), E(9, -1),F(10, -3),然后
用线段依次连接A,B,C,D,E,F,A各点;
(2)将(1)中所画图形先向左平移12个单位长度,再向
上平移5个单位长度,画出第二次平移后的图形;
(3)如何将(1)中所画图形经过一次平移得到(2)中所
画图形?平移前后对应点的横坐标有什么关系?
纵坐标呢?
随堂训练
(1)如图所示.
(2)如图所示.点拨:平移后各点坐标分别为A′(2,-3),
B′(3,-7),C′(4,-3),D′(5,-7),E′(6,-3).
(3)如图所示,连接AA′,由图可知
因此,将(1)中所画图形沿A到A′的方
向平移 个单位长度即可得到(2)
中所画图形;平移后的横坐标等于平
移前的横坐标加10,平移后的纵坐标
等于平移前的纵坐标减10.
解:
随堂训练
1.在平面直角坐标系中有一点A(-2,1),将点A先向右平移3个单位长度,再向下平移2个单位长度,则平移后点A的坐标____________.
(1,-1)
当堂检测
2.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是( )
A.(2,5) B.(-8,5)
C.(-8,-1) D.(2,-1)
D
当堂检测
3.如图,A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
A.2
B.3
C.4
D.5
A
当堂检测
4.我们知道:四边形不具有稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴的点D′处,则点C的对应点C′的坐标为( )
A.( ,1)
B.(2,1)
C.(1, )
D.(2, )
D
当堂检测
5.如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为( )
A.(a-2,b+3)
B.(a-2,b-3)
C.(a+2,b+3)
D.(a+2,b-3)
A
当堂检测
6.如图,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1).30 s后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )
A.Q′(2,3),R′(4,1)
B.Q′(2,3),R′(2,1)
C.Q′(2,2),R′(4,1)
D.Q′(3,3),R′(3,1)
A
当堂检测
7.如图,在平面直角坐标系中,等边三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
A.(4,2 )
B.(3,3 )
C.(4,3 )
D.(3,2 )
A
当堂检测
8.如图,已知点A(-1,0),B(1,1),把线段AB平移,使点B移动到点D(3,4)处,这时点A移动到点C处.
(1)画出平移后的线段CD,并写出点C的坐标;
(2)如果平移时只能左右或者上下移动,叙述线段AB是怎样移动到CD的;
(3)如果将CD看成是由AB经过
一次平移得到的,请指出这
一平移的平移方向和平移距
离.
当堂检测
(1)如图,C(1,3).
(2)(答案不唯一)AB向右平移2个单位长度,再向上平移3个单位长度即可得到CD.
(3)这一平移的平移方向是
由A到C的方向,平移
距离是 个单位长度.
当堂检测
图形的斜向平移,可通过左右平移和上下平移来完成.
课堂小结
第三章 图形的平移与旋转
第三章 图形的平移与旋转
3.1 图形的平移
(第3课时)
1.通过具体实例认识图形的两次平移变换,探索它的基本性质;(重点)
2.能按要求画出平面图形两次平移后的图形。(难点)
学习目标
点的平移与点的坐标变化规律:
左、右平移,横变纵不变,“右加左减”;
上、下平移,纵变横不变,“上加下减”.
知识回顾
在平面直角坐标系中,一个点沿x轴方向平移a
(a>0)个单位长度,再沿y轴方向平移b(b>0)个单位长度,得到点的坐标是什么?
知识讲解
1.两次平移的坐标变化规律
如图,将点A(-2, -3)向右平移5个单位长度,得到点A1,再向上平移6个单位,得到点A2,在图上标出这个点,并写出它的坐标.
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A1
(3, -3)
A
(-2, -3)
A2
(3, 3)
(-2, -3)
右移5个单位
(3, -3)
横坐标+5
(3, -3)
上移6个单位
(3, 3)
纵坐标+6
平移前后的坐标有什么关系
知识讲解
(1)点(x, y)向左平移a(a>0)个单位,再向上平移
b(b>0)个单位 平移后的坐标为(x-a, y+b);
(2)点(x, y)向右平移a(a>0)个单位,再向下平移
a(a>0)个单位 平移后的坐标为 (x+a, y-b);
规律
知识讲解
在平面直角坐标系中,有一点(1,3),要使它平移到点(-2,-2),应怎样平移?说出平移的路线.
提示:
点的斜向平移,可以通过点的左右和上下移动共同来完成
千万不要走斜线哦
随堂训练
(1, 3)
左移3个单位
(-2, 3)
横坐标-3
(-2, 3)
下移5个单位
(-2, -2)
纵坐标-5
- 5
- 4
- 3
- 2
- 6
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
x
- 5
- 4
- 3
- 2
- 7
- 6
- 1
- 1
(1,3)
(-2,-2)
y
方法一:
(1, 3)
下移5个单位
(1, -2)
纵坐标-5
(1, -2)
左移3个单位
(-2, -2)
横坐标-3
方法二:
随堂训练
一个图形依次沿 x轴方向、y轴方向平移后所得
图形与原来的图形相比, 位置有什么变化?它们对
应点的坐标之间有怎样的关系?
2.两次平移后的图形与原图形之间的平移方向、距离
知识讲解
一个图形依次沿x轴方向、y轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的.
总结
知识讲解
例2.如图,四边形ABCD各顶点的坐标分别为A(-3, 5),B(-4, 3),C (-1,1),D(-1,4),将四边形ABCD先向上平移3个单位长度, 再向右平移4个单位长度,得到四边形A′B′C′D′.
例题讲解
(1)四边形A′B′C′D′与四边形ABCD对应点的横坐标有 什么关系?纵坐标呢?分别写出点A', B', C',D'的 坐标;
(2)如果将四边形A′B′C′D′看成是由四边形ABCD经 过一次平移得到的,请指出这一平移的平移方向和平移距离.
知识讲解
(1)四边形A′B′C′D′与四边形ABCD相比,对应点的横
坐标分别增加了4, 纵坐标分别增加了3; A′(1,8),
B′(0, 6),C'(3, 4),D′(3, 7);
(2 )如图,连接AA′,由图可
知, AA′ =
因此,如果将四边形
A′B′C′D′看成是由四边形
ABCD经过一次平移得到
的,那么这一平移的平移
方向是由A到A′的方向,平移距离是5个单位长度.
解:
知识讲解
(1)在平面直角坐标系中描出点A( 6, 0),B(10, 3),
C(9, 1),D(12, 0), E(9, -1),F(10, -3),然后
用线段依次连接A,B,C,D,E,F,A各点;
(2)将(1)中所画图形先向左平移12个单位长度,再向
上平移5个单位长度,画出第二次平移后的图形;
(3)如何将(1)中所画图形经过一次平移得到(2)中所
画图形?平移前后对应点的横坐标有什么关系?
纵坐标呢?
随堂训练
(1)如图所示.
(2)如图所示.点拨:平移后各点坐标分别为A′(2,-3),
B′(3,-7),C′(4,-3),D′(5,-7),E′(6,-3).
(3)如图所示,连接AA′,由图可知
因此,将(1)中所画图形沿A到A′的方
向平移 个单位长度即可得到(2)
中所画图形;平移后的横坐标等于平
移前的横坐标加10,平移后的纵坐标
等于平移前的纵坐标减10.
解:
随堂训练
1.在平面直角坐标系中有一点A(-2,1),将点A先向右平移3个单位长度,再向下平移2个单位长度,则平移后点A的坐标____________.
(1,-1)
当堂检测
2.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是( )
A.(2,5) B.(-8,5)
C.(-8,-1) D.(2,-1)
D
当堂检测
3.如图,A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
A.2
B.3
C.4
D.5
A
当堂检测
4.我们知道:四边形不具有稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴的点D′处,则点C的对应点C′的坐标为( )
A.( ,1)
B.(2,1)
C.(1, )
D.(2, )
D
当堂检测
5.如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为( )
A.(a-2,b+3)
B.(a-2,b-3)
C.(a+2,b+3)
D.(a+2,b-3)
A
当堂检测
6.如图,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1).30 s后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )
A.Q′(2,3),R′(4,1)
B.Q′(2,3),R′(2,1)
C.Q′(2,2),R′(4,1)
D.Q′(3,3),R′(3,1)
A
当堂检测
7.如图,在平面直角坐标系中,等边三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
A.(4,2 )
B.(3,3 )
C.(4,3 )
D.(3,2 )
A
当堂检测
8.如图,已知点A(-1,0),B(1,1),把线段AB平移,使点B移动到点D(3,4)处,这时点A移动到点C处.
(1)画出平移后的线段CD,并写出点C的坐标;
(2)如果平移时只能左右或者上下移动,叙述线段AB是怎样移动到CD的;
(3)如果将CD看成是由AB经过
一次平移得到的,请指出这
一平移的平移方向和平移距
离.
当堂检测
(1)如图,C(1,3).
(2)(答案不唯一)AB向右平移2个单位长度,再向上平移3个单位长度即可得到CD.
(3)这一平移的平移方向是
由A到C的方向,平移
距离是 个单位长度.
当堂检测
图形的斜向平移,可通过左右平移和上下平移来完成.
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
