6.1.1 平行四边形的性质 教学课件 --北师大版初中数学八年级(下)
文档属性
| 名称 | 6.1.1 平行四边形的性质 教学课件 --北师大版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:00 | ||
图片预览





文档简介
(共22张PPT)
第六章 平行四边形
6.1.1 平行四边形的性质
第六章 平行四边形
学 习 目 标
1.知道平行四边形的有关概念.(重点)
2.掌握平行四边形的性质(中心对称图形、对边相等、对角相等).(重点)
情景导入
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形边的位置有什么特征?
知识回顾
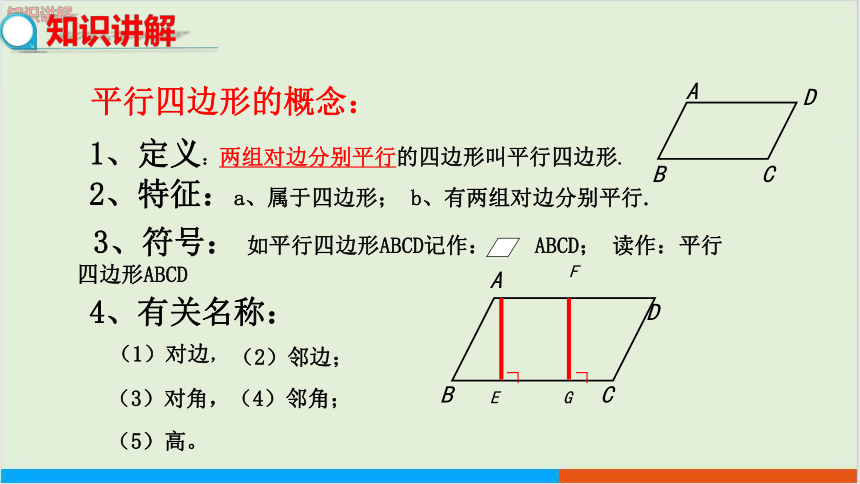
平行四边形的概念:
1、定义:两组对边分别平行的四边形叫平行四边形.
2、特征:a、属于四边形; b、有两组对边分别平行.
4、有关名称:
(3)对角,(4)邻角;
(5)高。
3、符号: 如平行四边形ABCD记作: ABCD; 读作:平行四边形ABCD
A
D
C
B
(1)对边,
(2)邻边;
∟
A
D
C
B
∟
E
F
G
知识讲解
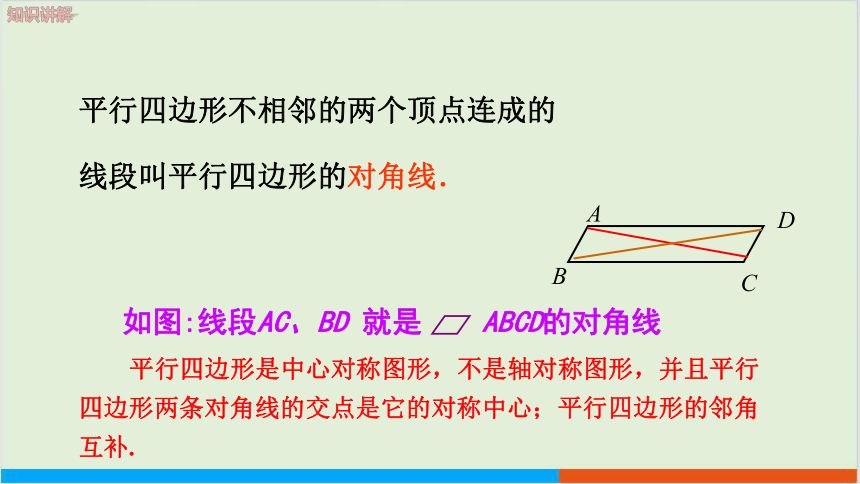
如图:线段AC、BD 就是 ABCD的对角线
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
平行四边形是中心对称图形,不是轴对称图形,并且平行四边形两条对角线的交点是它的对称中心;平行四边形的邻角互补.
A
B
C
D
F
E
G
H
O
3
如图: ABCD中,EF∥AB,
①则图中有__个平行四边形;
②若GH∥AD,EF与GH交于点O,
则图中有__个平行四边形。
9
随堂训练
1.平行四边形的边具有哪些性质?说说你的理由。
2.平行四边形的角具有哪些性质?说说你的理由。
A
B
C
D
知识讲解
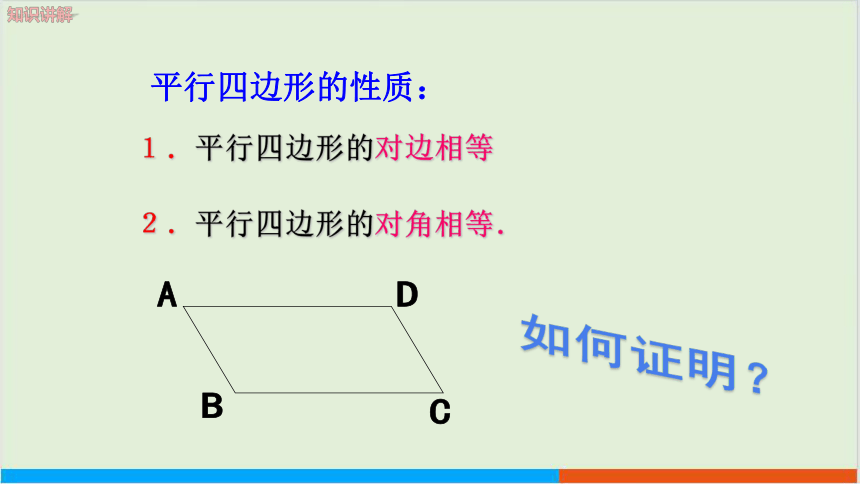
1.平行四边形的对边相等
平行四边形的性质:
2.平行四边形的对角相等.
如何证明?
A
B
C
D
B
D
C
A
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
分析:要证明AB=CD,BC=DA可转化全等三角形的对应边来证明,于是可作辅助线来达到目的.
证明:连结AC.
∵四边形ABCD是平行四边形,
∴AB∥CD,BC∥DA.
∴∠1=∠2, ∠3=∠4.
在△ABC和△CDA中
∠1=∠2, AC=CA, ∠3=∠4
∴△ABC≌△CDA(ASA).
∴AB=CD,BC=DA.
1
2
3
4
由上述证明过程你能得到平行四边形的对角相等吗?
定理1:平行四边形的对边相等.
平行四边形的对边平行.
∵四边形ABCD是平行四边形∴AB ∥ CD,BC ∥ AD.
∵四边形ABCD是平行四边形∴AB=CD,BC=AD.
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D.
A
B
C
D
例1.已知:如图, ABCD中,BE平分∠ABC
交AD于点E,
(1)如果AE=2,求CD的长;
(2)如果∠AEB=40°,求∠C的度数.
解:(1) ∵四边形ABCD是平行四边形,
∵BE平分∠ABC,
∴AD∥BC,
∴∠2=∠3
∴∠1=∠2,
∴∠1=∠3,
例题讲解
∴AB=AE=2,
又∵CD=AB,
∴CD=2;
(2)由(1)知: ∴∠1=∠3=40°,
∴∠A=180°-∠1-∠3=100°,
又∵∠C=∠A,
∴∠C=100°.
解:如图,∵∠A=60°,则∠A的对角∠C=60°,
又∵AB∥CD,∴∠D=180°-60°=120°.
同理可知∠B=120°.
A
B
C
D
1.在 ABCD中,已知∠A=60°,求∠B,∠C,∠D的度数.
随堂训练
解:∵平行四边形对边相等,
∴AB=CD=a,BC=AD=b,
∴四边形的周长为2a+2b.
A
B
C
D
2.在 ABCD中,已知AB=a,BC=b,求这个平行四边形的周长.
解:取AD中点F,连接EF,
∵BC=2AB,∴AB=BE=CD=CE,
又∵ AB∥EF∥CD ,
∴∠AED=∠EAB+∠EDC=∠AEB+∠DEC
∵ ∠AED+∠AEB+∠DEC=180°,
∴∠AEC=90°,∴AE⊥ED.
3.在 ABCD中,BC=2AB,点E为边BC的
中点.求证:AE⊥ED.
·
F
则AB∥EF∥CD.
平行四边形
定义:两组对边分别平行的四边形叫做
平行四边形.
性质
边
角
对边相等
对边平行
对角相等
邻角互补
中心对称图形
数学思想:“化归”
课堂小结
1. 在 □ABCD 中, ∠ A = 48°, BC = 3 cm, 求∠ B, ∠ C 的度数及 AD 边的长度.
当堂检测
2. 如图, 在 □ABCD 中, ∠ ADC = 125°, ∠ CAD = 21°, 求∠ ABC 和 ∠ CAB 的度数.
3. 已知: 如图, 在 □ABCD 中, E, F 分别 是 BC 和 AD 上的点, 且 BE = DF.
求证: △ ABE ≌ △ CDF.
4. 已知: 如图 , 在 □ABCD 中, ∠ ABC的 平分线交 CD 于点 E, ∠ ADC 的 平分线交 AB 于点 F. 求证: BF = DE.
第六章 平行四边形
6.1.1 平行四边形的性质
第六章 平行四边形
学 习 目 标
1.知道平行四边形的有关概念.(重点)
2.掌握平行四边形的性质(中心对称图形、对边相等、对角相等).(重点)
情景导入
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形边的位置有什么特征?
知识回顾
平行四边形的概念:
1、定义:两组对边分别平行的四边形叫平行四边形.
2、特征:a、属于四边形; b、有两组对边分别平行.
4、有关名称:
(3)对角,(4)邻角;
(5)高。
3、符号: 如平行四边形ABCD记作: ABCD; 读作:平行四边形ABCD
A
D
C
B
(1)对边,
(2)邻边;
∟
A
D
C
B
∟
E
F
G
知识讲解
如图:线段AC、BD 就是 ABCD的对角线
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
平行四边形是中心对称图形,不是轴对称图形,并且平行四边形两条对角线的交点是它的对称中心;平行四边形的邻角互补.
A
B
C
D
F
E
G
H
O
3
如图: ABCD中,EF∥AB,
①则图中有__个平行四边形;
②若GH∥AD,EF与GH交于点O,
则图中有__个平行四边形。
9
随堂训练
1.平行四边形的边具有哪些性质?说说你的理由。
2.平行四边形的角具有哪些性质?说说你的理由。
A
B
C
D
知识讲解
1.平行四边形的对边相等
平行四边形的性质:
2.平行四边形的对角相等.
如何证明?
A
B
C
D
B
D
C
A
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
分析:要证明AB=CD,BC=DA可转化全等三角形的对应边来证明,于是可作辅助线来达到目的.
证明:连结AC.
∵四边形ABCD是平行四边形,
∴AB∥CD,BC∥DA.
∴∠1=∠2, ∠3=∠4.
在△ABC和△CDA中
∠1=∠2, AC=CA, ∠3=∠4
∴△ABC≌△CDA(ASA).
∴AB=CD,BC=DA.
1
2
3
4
由上述证明过程你能得到平行四边形的对角相等吗?
定理1:平行四边形的对边相等.
平行四边形的对边平行.
∵四边形ABCD是平行四边形∴AB ∥ CD,BC ∥ AD.
∵四边形ABCD是平行四边形∴AB=CD,BC=AD.
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D.
A
B
C
D
例1.已知:如图, ABCD中,BE平分∠ABC
交AD于点E,
(1)如果AE=2,求CD的长;
(2)如果∠AEB=40°,求∠C的度数.
解:(1) ∵四边形ABCD是平行四边形,
∵BE平分∠ABC,
∴AD∥BC,
∴∠2=∠3
∴∠1=∠2,
∴∠1=∠3,
例题讲解
∴AB=AE=2,
又∵CD=AB,
∴CD=2;
(2)由(1)知: ∴∠1=∠3=40°,
∴∠A=180°-∠1-∠3=100°,
又∵∠C=∠A,
∴∠C=100°.
解:如图,∵∠A=60°,则∠A的对角∠C=60°,
又∵AB∥CD,∴∠D=180°-60°=120°.
同理可知∠B=120°.
A
B
C
D
1.在 ABCD中,已知∠A=60°,求∠B,∠C,∠D的度数.
随堂训练
解:∵平行四边形对边相等,
∴AB=CD=a,BC=AD=b,
∴四边形的周长为2a+2b.
A
B
C
D
2.在 ABCD中,已知AB=a,BC=b,求这个平行四边形的周长.
解:取AD中点F,连接EF,
∵BC=2AB,∴AB=BE=CD=CE,
又∵ AB∥EF∥CD ,
∴∠AED=∠EAB+∠EDC=∠AEB+∠DEC
∵ ∠AED+∠AEB+∠DEC=180°,
∴∠AEC=90°,∴AE⊥ED.
3.在 ABCD中,BC=2AB,点E为边BC的
中点.求证:AE⊥ED.
·
F
则AB∥EF∥CD.
平行四边形
定义:两组对边分别平行的四边形叫做
平行四边形.
性质
边
角
对边相等
对边平行
对角相等
邻角互补
中心对称图形
数学思想:“化归”
课堂小结
1. 在 □ABCD 中, ∠ A = 48°, BC = 3 cm, 求∠ B, ∠ C 的度数及 AD 边的长度.
当堂检测
2. 如图, 在 □ABCD 中, ∠ ADC = 125°, ∠ CAD = 21°, 求∠ ABC 和 ∠ CAB 的度数.
3. 已知: 如图, 在 □ABCD 中, E, F 分别 是 BC 和 AD 上的点, 且 BE = DF.
求证: △ ABE ≌ △ CDF.
4. 已知: 如图 , 在 □ABCD 中, ∠ ABC的 平分线交 CD 于点 E, ∠ ADC 的 平分线交 AB 于点 F. 求证: BF = DE.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
