6.2.2 平行四边形的性质 教学课件 --北师大版初中数学八年级(下)
文档属性
| 名称 | 6.2.2 平行四边形的性质 教学课件 --北师大版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:00 | ||
图片预览


文档简介
(共15张PPT)
第六章 平行四边形
6.2.2平行四边形的性质
第六章 平行四边形
学 习 目 标
1、探索并证明“对角线互相平分的四边形是平行四边形”;(重点)
2、应用平行四边形的判定定理解决问题.(难点)
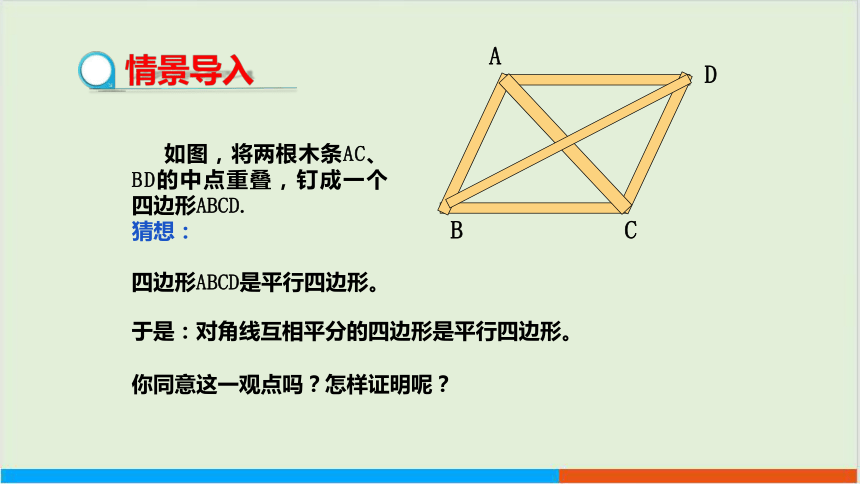
如图,将两根木条AC、BD的中点重叠,钉成一个四边形ABCD.
猜想:
A
B
C
D
四边形ABCD是平行四边形。
于是:对角线互相平分的四边形是平行四边形。
你同意这一观点吗?怎样证明呢?
情景导入
B
D
A
C
O
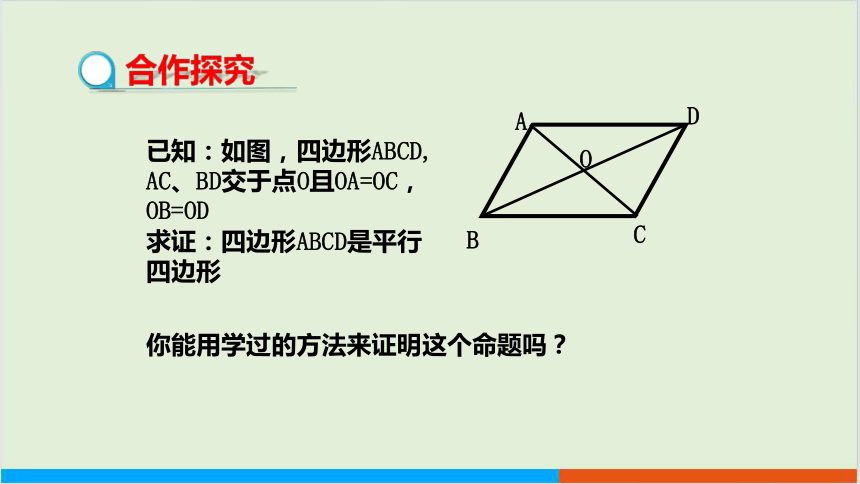
你能用学过的方法来证明这个命题吗?
已知:如图,四边形ABCD, AC、BD交于点O且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
合作探究
B
D
A
C
O
4
2
1
3
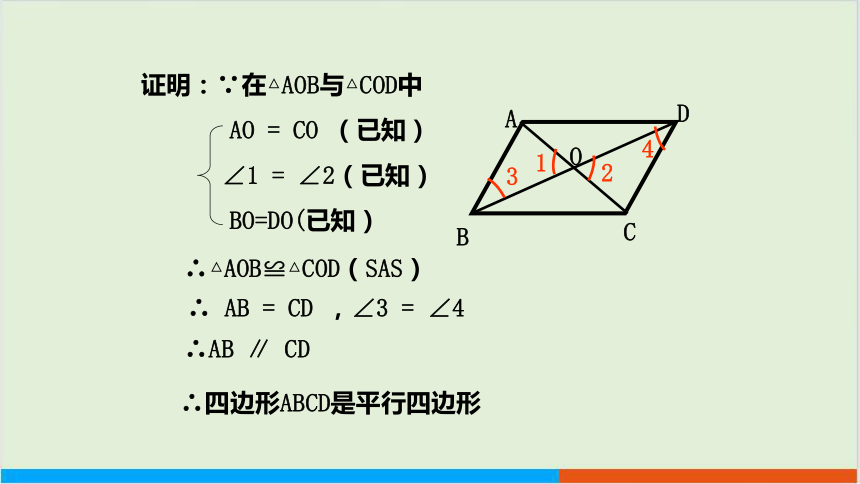
证明:∵在△AOB与△COD中
AO = CO (已知)
∠1 = ∠2(已知)
BO=DO(已知)
∴△AOB≌△COD(SAS)
∴ AB = CD ,∠3 = ∠4
∴AB ∥ CD
∴四边形ABCD是平行四边形
符号语言:
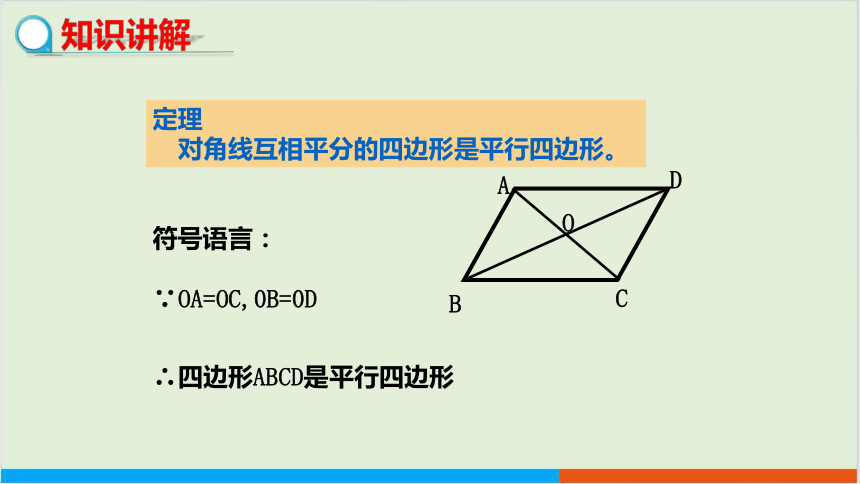
∴四边形ABCD是平行四边形
定理
对角线互相平分的四边形是平行四边形。
∵OA=OC,0B=0D
B
D
A
C
O
知识讲解
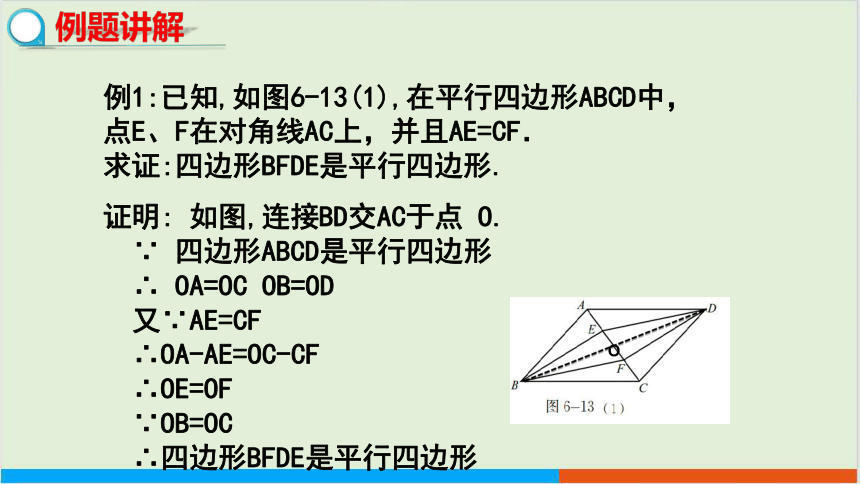
例1:已知,如图6-13(1),在平行四边形ABCD中,
点E、F在对角线AC上,并且AE=CF.
求证:四边形BFDE是平行四边形.
证明: 如图,连接BD交AC于点 O.
∵ 四边形ABCD是平行四边形
∴ OA=OC OB=OD
又∵AE=CF
∴OA-AE=OC-CF
∴OE=OF
∵OB=OC
∴四边形BFDE是平行四边形
O
例题讲解
对于上述例题,若E,F继续移动至OA,OC的延长线上,
仍使AE=CF(如图),则结论还成立吗?若成立,请证明.
随堂训练
从边来判定
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
课堂小结
1.如图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC=___ _cm,CD=___ _cm时,四边形ABCD为平行四边形;
(2)若AC=8cm,BD=10cm,那么当AO=__ _cm,DO=__ _cm时,四边形ABCD为平行四边形.
8
4
4
5
当堂检测
2. 对于四边形ABCD,如果从条件①AB∥CD
②AD∥BC③AB=CD④BC=AD中选出2个,
那么能说明四边形ABCD是平行四边形的有
_______(填序号,填出符合条件的一种情
况即可)
3.若对角线AC、BD相交于点O,
且OA=OC,则只需添加一个
条件_____能说明四边形ABCD是平行
四边形.
3.请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
100°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
4 .已知:如图,平行四边形ABCD的对角线AC与BD
交于点O,E、F分别是OA、OC的中点。
求证:四边形BFDE是平行四边形。
B
C
A
D
E
F
O
解:(1)分别过点A,C作BC,BA的平行线,两平行线相交于点D,连接AD,CD,则四边形ABCD即为原来的平行四边形.
5 如图所示,有一块平行四边形玻璃镜片,不小心打掉了一块,但是有两条边是完好的.同学们想想看,有没有办法把原来的平行四边形重新画出来
(2)分别以点A,C为圆心,以BC,BA的长为半径画弧,两弧相交于点D,连接AD,CD,则四边形ABCD即为原来的平行四边形.
(3)连接AC,取AC的中点O,再连接BO,并延长BO到D,使DO=BO,连接AD,CD,则四边形ABCD即为原来的平行四边形.
第六章 平行四边形
6.2.2平行四边形的性质
第六章 平行四边形
学 习 目 标
1、探索并证明“对角线互相平分的四边形是平行四边形”;(重点)
2、应用平行四边形的判定定理解决问题.(难点)
如图,将两根木条AC、BD的中点重叠,钉成一个四边形ABCD.
猜想:
A
B
C
D
四边形ABCD是平行四边形。
于是:对角线互相平分的四边形是平行四边形。
你同意这一观点吗?怎样证明呢?
情景导入
B
D
A
C
O
你能用学过的方法来证明这个命题吗?
已知:如图,四边形ABCD, AC、BD交于点O且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
合作探究
B
D
A
C
O
4
2
1
3
证明:∵在△AOB与△COD中
AO = CO (已知)
∠1 = ∠2(已知)
BO=DO(已知)
∴△AOB≌△COD(SAS)
∴ AB = CD ,∠3 = ∠4
∴AB ∥ CD
∴四边形ABCD是平行四边形
符号语言:
∴四边形ABCD是平行四边形
定理
对角线互相平分的四边形是平行四边形。
∵OA=OC,0B=0D
B
D
A
C
O
知识讲解
例1:已知,如图6-13(1),在平行四边形ABCD中,
点E、F在对角线AC上,并且AE=CF.
求证:四边形BFDE是平行四边形.
证明: 如图,连接BD交AC于点 O.
∵ 四边形ABCD是平行四边形
∴ OA=OC OB=OD
又∵AE=CF
∴OA-AE=OC-CF
∴OE=OF
∵OB=OC
∴四边形BFDE是平行四边形
O
例题讲解
对于上述例题,若E,F继续移动至OA,OC的延长线上,
仍使AE=CF(如图),则结论还成立吗?若成立,请证明.
随堂训练
从边来判定
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
课堂小结
1.如图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC=___ _cm,CD=___ _cm时,四边形ABCD为平行四边形;
(2)若AC=8cm,BD=10cm,那么当AO=__ _cm,DO=__ _cm时,四边形ABCD为平行四边形.
8
4
4
5
当堂检测
2. 对于四边形ABCD,如果从条件①AB∥CD
②AD∥BC③AB=CD④BC=AD中选出2个,
那么能说明四边形ABCD是平行四边形的有
_______(填序号,填出符合条件的一种情
况即可)
3.若对角线AC、BD相交于点O,
且OA=OC,则只需添加一个
条件_____能说明四边形ABCD是平行
四边形.
3.请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
100°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
4 .已知:如图,平行四边形ABCD的对角线AC与BD
交于点O,E、F分别是OA、OC的中点。
求证:四边形BFDE是平行四边形。
B
C
A
D
E
F
O
解:(1)分别过点A,C作BC,BA的平行线,两平行线相交于点D,连接AD,CD,则四边形ABCD即为原来的平行四边形.
5 如图所示,有一块平行四边形玻璃镜片,不小心打掉了一块,但是有两条边是完好的.同学们想想看,有没有办法把原来的平行四边形重新画出来
(2)分别以点A,C为圆心,以BC,BA的长为半径画弧,两弧相交于点D,连接AD,CD,则四边形ABCD即为原来的平行四边形.
(3)连接AC,取AC的中点O,再连接BO,并延长BO到D,使DO=BO,连接AD,CD,则四边形ABCD即为原来的平行四边形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
