勾股定理(1)
图片预览







文档简介
课件25张PPT。 读一读
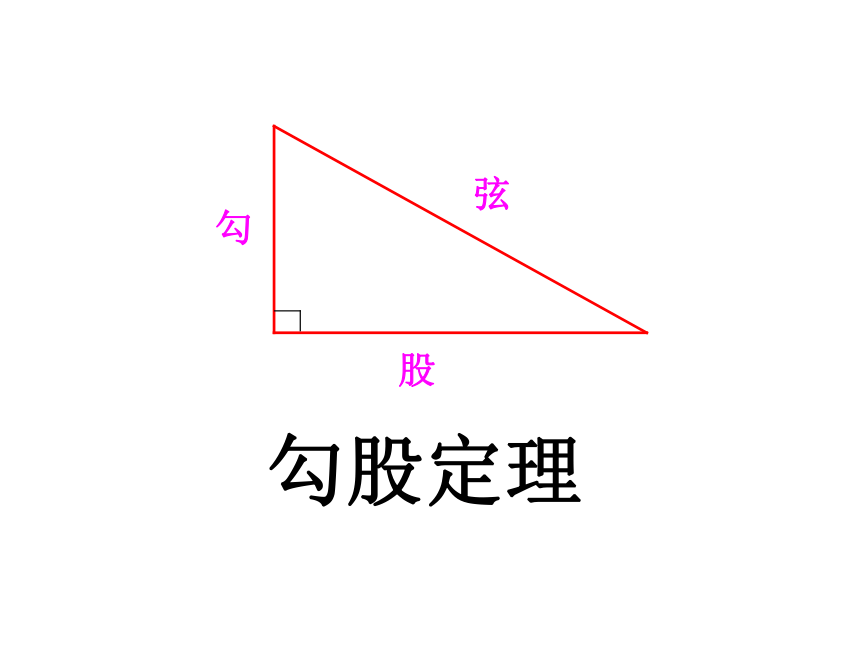
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
图1-1图1-2hdzh18.1勾股定理 在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”即:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。故称之为“勾股定理”或“商高定理”史话勾股定理勾股定理勾股弦 在西方,希腊数学家欧几里德(Euclid,公元前三百年左右)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了。 毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年。 相传,毕达哥拉斯学派找到了勾股定理的证明后,欣喜若狂,杀了一百头牛祭神,由此,又有“百牛定理”之称。教学目标※探索直角三角形三边关系,掌握勾股定理的运用思想,发展几何思维。※经历观察与发现直角三角形三边关系的 过程,感受勾股定理的应用意识。※培养严谨的数学学习的态度,体会勾股定理的应用价值。毕达哥拉斯
(公元前572----前492年),
古希腊著名的哲学家、数学家、天文学家。 相传在2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系,我们一起来观察图中的地面,看看能发现什么。
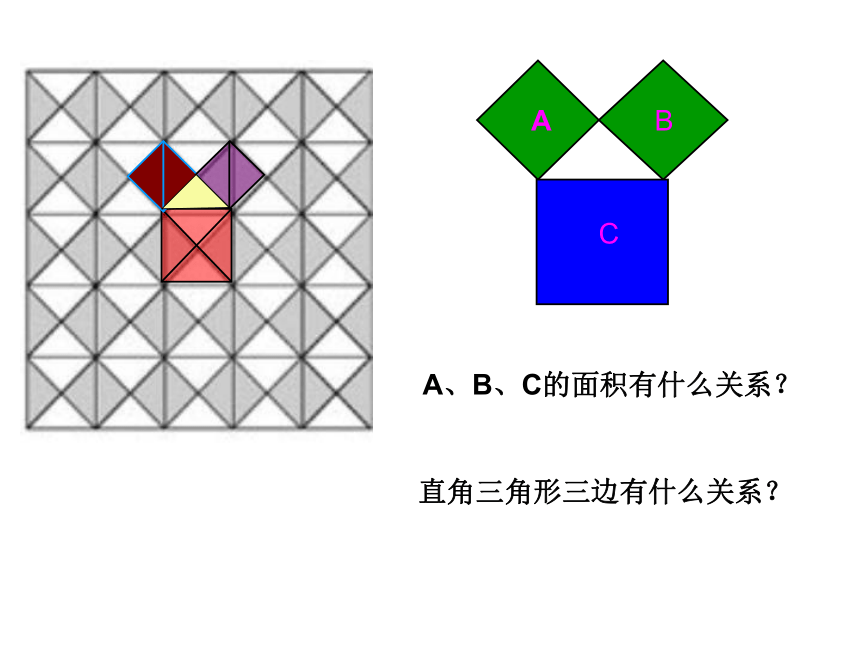
A、B、C的面积有什么关系?直角三角形三边有什么关系?图1—199991818A的面积+ B的面积= C的面积图1—2444488A的面积+ B的面积= C的面积 因此可知等腰直角三角形有这样的性质:
对于任意直角三角形都有这样的性质吗?两直边的平方和等于斜边的平方看下图图1图2491392534sA+sB=sC 两直角边的平方和
等于斜边的平方abcc2=a2 + b2结论变形815A49B251.求下列图中字母所代表的正方形的面积:学以致用,做一做结论:S1+S2+S3+S4=S5+S6=S7学海无涯 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和S1S2解:∵ SE= 49S1=SA+SBS2=SC+SD∴ SA+SB+SC+SD
= S1+S2 = SE = 49美丽的勾股树2.求出下列直角三角形中未知边的长度5x13学以致用,做一做解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2X2 =36+64x2 =100x2=62+82∴ x=10 ∵x>0 x2+52=132 x2=132-52x2=144∴ x=12(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2∵x>0ACBACB生活中的数学问题一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2m1m探究12m1m分析 连结AC,在Rt△ABC中,根据勾股定理:
因此,
因为AC大于木板的宽,
所以木板能从门框内通过。1.在△ABC中, ∠C=90°,a=6,b=8,
则c=____2.在△ABC中, a=6,b=8,试求第三边c的值10练一练3.在一个直角三角形中, 两边长分别为6、
8,则第三边的长为________10 练一练或课堂小结⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.⒊勾股定理的主要作用是 在直角三角形中,已知任意两边求第三边的长。作业:P69---70 1、2、3。
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
图1-1图1-2hdzh18.1勾股定理 在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”即:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。故称之为“勾股定理”或“商高定理”史话勾股定理勾股定理勾股弦 在西方,希腊数学家欧几里德(Euclid,公元前三百年左右)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了。 毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年。 相传,毕达哥拉斯学派找到了勾股定理的证明后,欣喜若狂,杀了一百头牛祭神,由此,又有“百牛定理”之称。教学目标※探索直角三角形三边关系,掌握勾股定理的运用思想,发展几何思维。※经历观察与发现直角三角形三边关系的 过程,感受勾股定理的应用意识。※培养严谨的数学学习的态度,体会勾股定理的应用价值。毕达哥拉斯
(公元前572----前492年),
古希腊著名的哲学家、数学家、天文学家。 相传在2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系,我们一起来观察图中的地面,看看能发现什么。
A、B、C的面积有什么关系?直角三角形三边有什么关系?图1—199991818A的面积+ B的面积= C的面积图1—2444488A的面积+ B的面积= C的面积 因此可知等腰直角三角形有这样的性质:
对于任意直角三角形都有这样的性质吗?两直边的平方和等于斜边的平方看下图图1图2491392534sA+sB=sC 两直角边的平方和
等于斜边的平方abcc2=a2 + b2结论变形815A49B251.求下列图中字母所代表的正方形的面积:学以致用,做一做结论:S1+S2+S3+S4=S5+S6=S7学海无涯 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和S1S2解:∵ SE= 49S1=SA+SBS2=SC+SD∴ SA+SB+SC+SD
= S1+S2 = SE = 49美丽的勾股树2.求出下列直角三角形中未知边的长度5x13学以致用,做一做解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2X2 =36+64x2 =100x2=62+82∴ x=10 ∵x>0 x2+52=132 x2=132-52x2=144∴ x=12(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2∵x>0ACBACB生活中的数学问题一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2m1m探究12m1m分析 连结AC,在Rt△ABC中,根据勾股定理:
因此,
因为AC大于木板的宽,
所以木板能从门框内通过。1.在△ABC中, ∠C=90°,a=6,b=8,
则c=____2.在△ABC中, a=6,b=8,试求第三边c的值10练一练3.在一个直角三角形中, 两边长分别为6、
8,则第三边的长为________10 练一练或课堂小结⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.⒊勾股定理的主要作用是 在直角三角形中,已知任意两边求第三边的长。作业:P69---70 1、2、3。
