6.4.1 多边形的内角和与外角和 教学课件 --北师大版初中数学八年级(下)
文档属性
| 名称 | 6.4.1 多边形的内角和与外角和 教学课件 --北师大版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:00 | ||
图片预览





文档简介
(共24张PPT)
第六章 平行四边形
6.4.1多边形的内角和与外角和
第六章 平行四边形
学 习 目 标
1掌握多边形内角和定理,进一步了解转化的数学思想;(重点)
2、经历探索多边形的内角和公式的过程;会应用公式解决问题。(难点)
1.△ABC中,∠A=50°,∠B=30°,则∠C=_____°;
2.正方形的内角和等于多少度?长方形呢?
100
3.如图,对于任意形状的四边形它的内角和是多少度呢?你是怎么得到的?
知识回顾
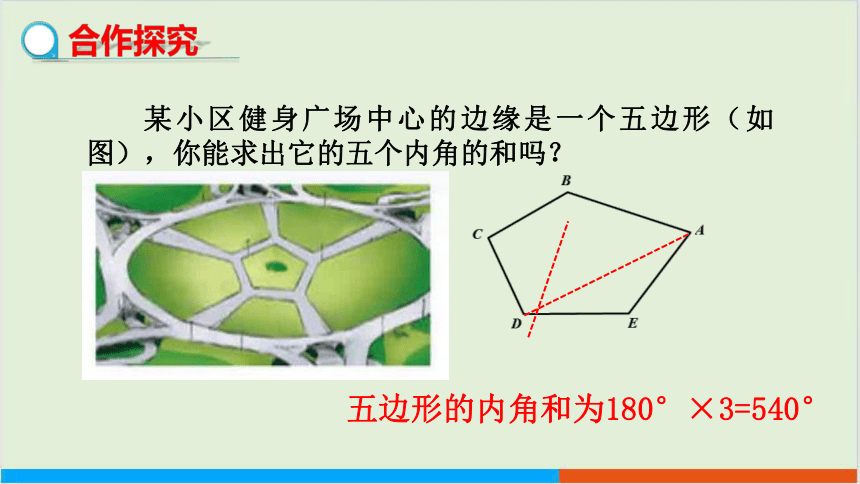
某小区健身广场中心的边缘是一个五边形(如图),你能求出它的五个内角的和吗?
五边形的内角和为180°×3=540°
合作探究
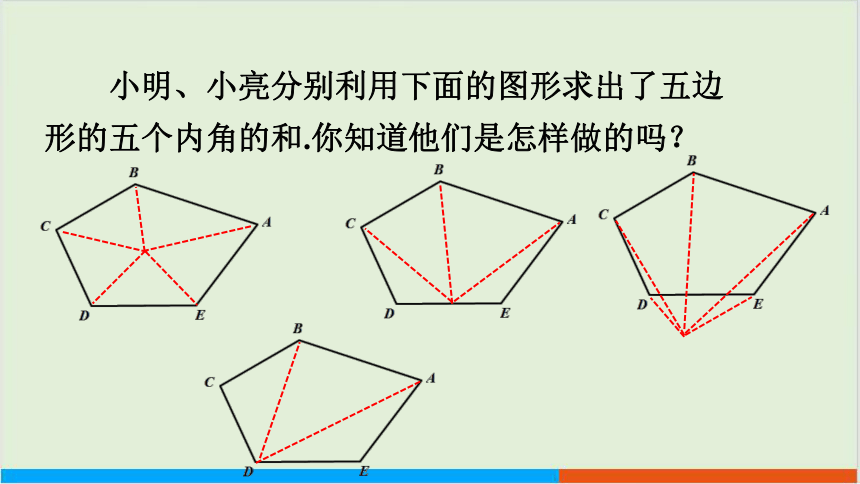
小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
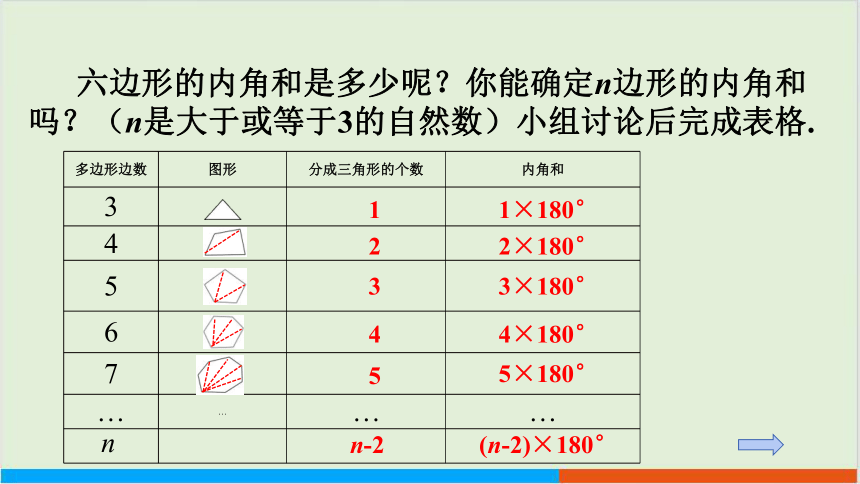
六边形的内角和是多少呢?你能确定n边形的内角和吗?(n是大于或等于3的自然数)小组讨论后完成表格.
3×180°
多边形边数 图形 分成三角形的个数 内角和
3
4
5
6
7
… … … …
1
2
3
4
n-2
1×180°
2×180°
(n-2)×180°
4×180°
5×180°
n
5
n边形的内角和等于(n-2)·180°
多边形内角和定理:
知识讲解
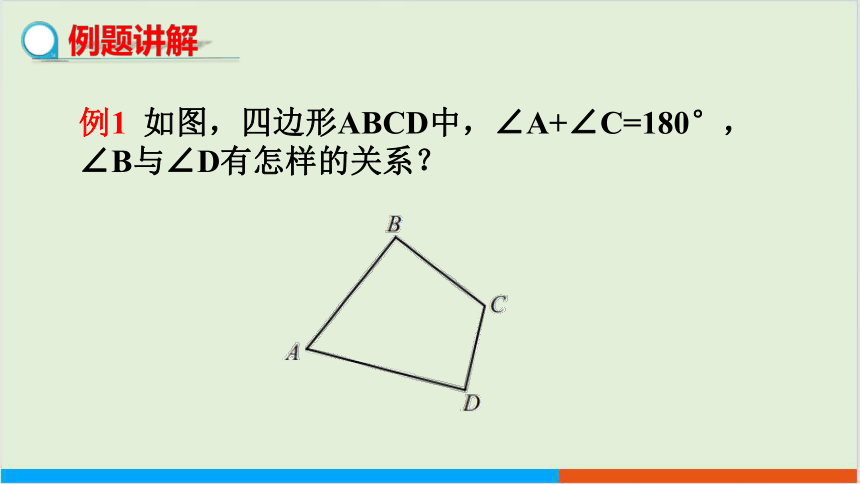
例1 如图,四边形ABCD中,∠A+∠C=180°,∠B与∠D有怎样的关系?
例题讲解
例2 一个多边形的内角和为1440°,则它是几边形?
解:设这个多边形是n边形,则
180°·(n-2)=1440°
∴ n=10
∴ 这个多边形是10边形
例题讲解
1.六边形的内角和为( )
A.1260° B.1080° C.900° D.720°
2.下列角度中能成为某多边形的内角和的是( )
A.270° B.560° C.1 800° D.1 900°
3.八边形的七个内角都为150°,则第八个内角=________
4.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形是几边形?它的内角和是多少?21·
C
D
30°
七边形,内角和为900°
随堂训练
1.正三角形(等边三角形)的内角和等于多少度?
每个内角等于多少度?你是怎么计算的?
2.正四边形(正方形)的内角和等于多少度?每个内角等于多少度?你是怎么计算的?
3.正五边形、正六边形、正八边形呢···正n边形呢?
合作探究
正n边形的每个内角度数为:
知识讲解
1.正八边形的每个内角都是( )
A.60° B.80° C.100° D.135°
2.一个多边形的每个内角均为120°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
D
C
随堂训练
截去一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
拓展延伸
剪去一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
剪去一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
剪去一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
1、多边形的内角和定理:n边形的内角和等于(n-2)·180°
2、正多边形内角的度数:
课堂小结
1.一个多边形的内角和为1080°,则这个多边形的边数为( )
A.9 B.8 C.7 D.6
2.若一个多边形的每个内角都为108°,则这个多边形的边数是( )
A.8 B.7 C.6 D.5
3.正十二边形每个内角的度数为_____________
B
D
150°
当堂检测
4.一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5 B.5或6 C.5或7 D.5或6或7
D
5.小彬求出一个正多边形的一个内角为145°,他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由.
解:不正确.
设该正多边形的边数为n,如果结果正确,则
145°n=180°(n-2)
解得n=
6.有两个多边形,边数之比为3﹕4,内角和之比为1﹕2,求这两个多边形的边数.
3,4
7.如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,如何知道模板是否合格?为什么?
不合格
第六章 平行四边形
6.4.1多边形的内角和与外角和
第六章 平行四边形
学 习 目 标
1掌握多边形内角和定理,进一步了解转化的数学思想;(重点)
2、经历探索多边形的内角和公式的过程;会应用公式解决问题。(难点)
1.△ABC中,∠A=50°,∠B=30°,则∠C=_____°;
2.正方形的内角和等于多少度?长方形呢?
100
3.如图,对于任意形状的四边形它的内角和是多少度呢?你是怎么得到的?
知识回顾
某小区健身广场中心的边缘是一个五边形(如图),你能求出它的五个内角的和吗?
五边形的内角和为180°×3=540°
合作探究
小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
六边形的内角和是多少呢?你能确定n边形的内角和吗?(n是大于或等于3的自然数)小组讨论后完成表格.
3×180°
多边形边数 图形 分成三角形的个数 内角和
3
4
5
6
7
… … … …
1
2
3
4
n-2
1×180°
2×180°
(n-2)×180°
4×180°
5×180°
n
5
n边形的内角和等于(n-2)·180°
多边形内角和定理:
知识讲解
例1 如图,四边形ABCD中,∠A+∠C=180°,∠B与∠D有怎样的关系?
例题讲解
例2 一个多边形的内角和为1440°,则它是几边形?
解:设这个多边形是n边形,则
180°·(n-2)=1440°
∴ n=10
∴ 这个多边形是10边形
例题讲解
1.六边形的内角和为( )
A.1260° B.1080° C.900° D.720°
2.下列角度中能成为某多边形的内角和的是( )
A.270° B.560° C.1 800° D.1 900°
3.八边形的七个内角都为150°,则第八个内角=________
4.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形是几边形?它的内角和是多少?21·
C
D
30°
七边形,内角和为900°
随堂训练
1.正三角形(等边三角形)的内角和等于多少度?
每个内角等于多少度?你是怎么计算的?
2.正四边形(正方形)的内角和等于多少度?每个内角等于多少度?你是怎么计算的?
3.正五边形、正六边形、正八边形呢···正n边形呢?
合作探究
正n边形的每个内角度数为:
知识讲解
1.正八边形的每个内角都是( )
A.60° B.80° C.100° D.135°
2.一个多边形的每个内角均为120°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
D
C
随堂训练
截去一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
拓展延伸
剪去一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
剪去一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
剪去一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
1、多边形的内角和定理:n边形的内角和等于(n-2)·180°
2、正多边形内角的度数:
课堂小结
1.一个多边形的内角和为1080°,则这个多边形的边数为( )
A.9 B.8 C.7 D.6
2.若一个多边形的每个内角都为108°,则这个多边形的边数是( )
A.8 B.7 C.6 D.5
3.正十二边形每个内角的度数为_____________
B
D
150°
当堂检测
4.一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5 B.5或6 C.5或7 D.5或6或7
D
5.小彬求出一个正多边形的一个内角为145°,他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由.
解:不正确.
设该正多边形的边数为n,如果结果正确,则
145°n=180°(n-2)
解得n=
6.有两个多边形,边数之比为3﹕4,内角和之比为1﹕2,求这两个多边形的边数.
3,4
7.如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,如何知道模板是否合格?为什么?
不合格
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
