1.4 整式的乘法(第2课时)教学课件 北师大版中学数学七年级(下)
文档属性
| 名称 | 1.4 整式的乘法(第2课时)教学课件 北师大版中学数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:07:33 | ||
图片预览





文档简介
(共18张PPT)
第 一 章 整式的乘除
第一章 整式的乘除
1.4 整式的乘法
第2课时 单项式与多项式相乘
学 习 目 标
1.能根据乘法分配律和单项式与单项式相乘的法则,
探究单项式与多项式相乘的法则; (重点)
2.掌握单项式与多项式相乘的法则并会运用. (难点)
知识回顾
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
1.单项式与单项式的乘法法则
在多项式中,每个单项式叫做多项式的项。
2. 什么叫多项式的项
请说出多项式3x2+2x+5的项和各项系数
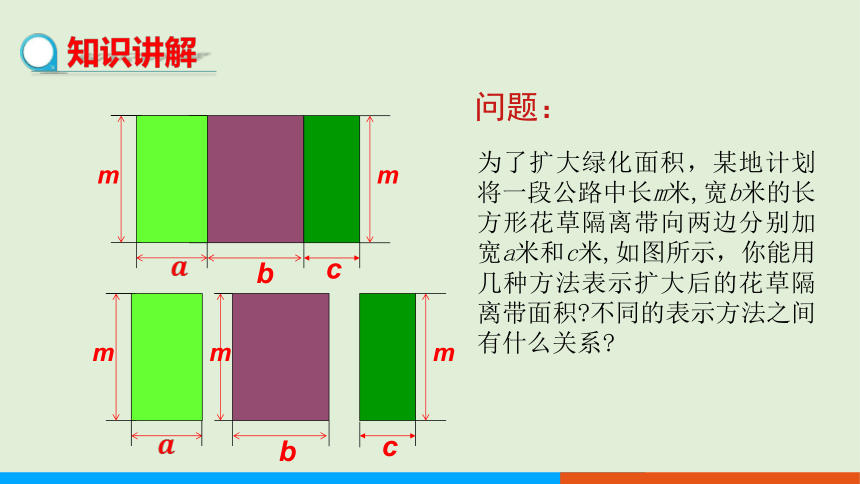
为了扩大绿化面积,某地计划将一段公路中长m米,宽b米的长方形花草隔离带向两边分别加宽a米和c米,如图所示,你能用几种方法表示扩大后的花草隔离带面积 不同的表示方法之间有什么关系
m
b
m
m
c
m
b
m
c
m
问题:
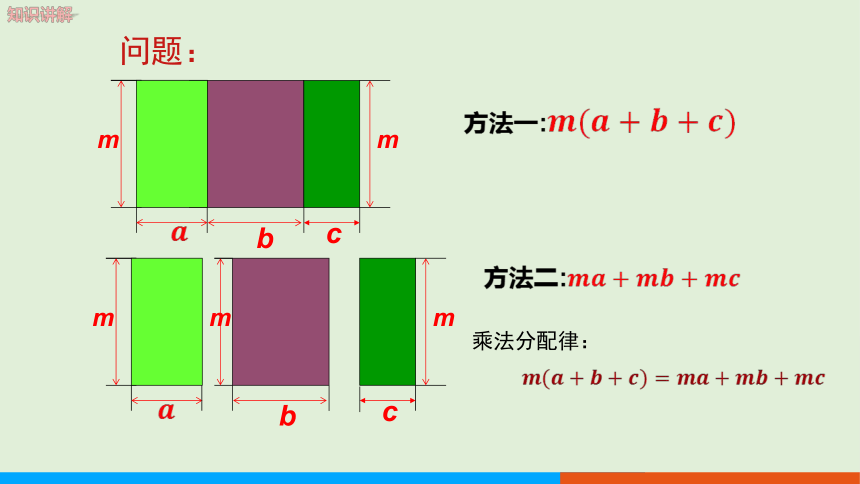
知识讲解
m
b
m
m
c
方法一:
m
b
m
c
m
方法二:
问题:
乘法分配律:
如何计算:(-42)·(3+2)
思考:
(利用乘法的分配律转化为单项式乘单项式)
单项式与多项式相乘,就是根据乘法分配律用单项式去乘多项式的每一项,再把所得的积相加.
用字母表示如下:
注意:(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同.
单项式与多项式的乘法法则
p(a+b+c)=pa+pb+pc
例1
计算:
(1)2ab(5ab2+3a2b);
(2)( -2ab)·
(3)5m2n(2n+3m-n2);
解:(1)原式=2ab·5ab2+2ab·3a2b
(2)原式=
(3)原式=5m2n·2n+5m2n·3m+5m2n·(-n2)
=10m2n2+15m3n-5m2n3;
(4)原式=(2x+2y2z+2xy2z3)·xyz
(4)2(x+y2z+xy2z3)·xyz;
=2x2yz+2xy3z2+2x2y3z4.
跟踪练习
计算:
化简求值:-22·(2)-5(2),
其中=1,=-1.
解:原式=-2-22-5+
=-2-2-5+
=-7+3.
当=1,=-1 时,
原式=-7×13×(-1)+3×12×(-1)2
=-7×1×(-1)+3×1×1
=7+3=10.
例2
随堂训练
1.下列计算错误的是( )
(A)5(22-)=103-5
(B)-3+ 4-=-
(C)2=8
(D)(--12) (-)2=+2
D
=(--12) ()
=-+1+2
2.判断
×
×
)=( )
( )
(-2) (-3)=-22-2( )
×
3.计算:
注意:(1)多项式每一项要包括前面的符号;
(2)单项式必须与多项式中每一项相乘,结果的项数与原多项式项数一致;
(3)单项式系数为负时,改变多项式每项的符号.
4.计算:
-22·(2)-5(-)
解:原式=-
=-
=-7.
5.先化简,再求值3a(2a2-4a+3)-2a2(3a+4),其中
a=-2.
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
当a=-2时,原式=-20×(-2)2+9×(-2)=-98.
6.如果(-3x)2(x2-2nx+2)的展开式中不含x3 项, 求n的值.
解: (-3x)2(x2-2nx+2)
=9x2(x2-2nx+2)
=9x4-18nx3+18x2.
∵展开式中不含x3项,∴n=0.
课堂小结
单项式乘多项式
实质上是转化为单项式×单项式
注意
整式的乘法
(1)计算时,要注意符号问题,多项式中每一项都
包括它前面的符号,单项式分别与多项式的每
一项相乘时,同号相乘得正,异号相乘得负
(2)不要出现漏乘现象
(3)运算要有顺序:先乘方,再乘除,最后加减
(4)对于混合运算,注意最后应合并同类项
第 一 章 整式的乘除
第一章 整式的乘除
1.4 整式的乘法
第2课时 单项式与多项式相乘
学 习 目 标
1.能根据乘法分配律和单项式与单项式相乘的法则,
探究单项式与多项式相乘的法则; (重点)
2.掌握单项式与多项式相乘的法则并会运用. (难点)
知识回顾
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
1.单项式与单项式的乘法法则
在多项式中,每个单项式叫做多项式的项。
2. 什么叫多项式的项
请说出多项式3x2+2x+5的项和各项系数
为了扩大绿化面积,某地计划将一段公路中长m米,宽b米的长方形花草隔离带向两边分别加宽a米和c米,如图所示,你能用几种方法表示扩大后的花草隔离带面积 不同的表示方法之间有什么关系
m
b
m
m
c
m
b
m
c
m
问题:
知识讲解
m
b
m
m
c
方法一:
m
b
m
c
m
方法二:
问题:
乘法分配律:
如何计算:(-42)·(3+2)
思考:
(利用乘法的分配律转化为单项式乘单项式)
单项式与多项式相乘,就是根据乘法分配律用单项式去乘多项式的每一项,再把所得的积相加.
用字母表示如下:
注意:(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同.
单项式与多项式的乘法法则
p(a+b+c)=pa+pb+pc
例1
计算:
(1)2ab(5ab2+3a2b);
(2)( -2ab)·
(3)5m2n(2n+3m-n2);
解:(1)原式=2ab·5ab2+2ab·3a2b
(2)原式=
(3)原式=5m2n·2n+5m2n·3m+5m2n·(-n2)
=10m2n2+15m3n-5m2n3;
(4)原式=(2x+2y2z+2xy2z3)·xyz
(4)2(x+y2z+xy2z3)·xyz;
=2x2yz+2xy3z2+2x2y3z4.
跟踪练习
计算:
化简求值:-22·(2)-5(2),
其中=1,=-1.
解:原式=-2-22-5+
=-2-2-5+
=-7+3.
当=1,=-1 时,
原式=-7×13×(-1)+3×12×(-1)2
=-7×1×(-1)+3×1×1
=7+3=10.
例2
随堂训练
1.下列计算错误的是( )
(A)5(22-)=103-5
(B)-3+ 4-=-
(C)2=8
(D)(--12) (-)2=+2
D
=(--12) ()
=-+1+2
2.判断
×
×
)=( )
( )
(-2) (-3)=-22-2( )
×
3.计算:
注意:(1)多项式每一项要包括前面的符号;
(2)单项式必须与多项式中每一项相乘,结果的项数与原多项式项数一致;
(3)单项式系数为负时,改变多项式每项的符号.
4.计算:
-22·(2)-5(-)
解:原式=-
=-
=-7.
5.先化简,再求值3a(2a2-4a+3)-2a2(3a+4),其中
a=-2.
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
当a=-2时,原式=-20×(-2)2+9×(-2)=-98.
6.如果(-3x)2(x2-2nx+2)的展开式中不含x3 项, 求n的值.
解: (-3x)2(x2-2nx+2)
=9x2(x2-2nx+2)
=9x4-18nx3+18x2.
∵展开式中不含x3项,∴n=0.
课堂小结
单项式乘多项式
实质上是转化为单项式×单项式
注意
整式的乘法
(1)计算时,要注意符号问题,多项式中每一项都
包括它前面的符号,单项式分别与多项式的每
一项相乘时,同号相乘得正,异号相乘得负
(2)不要出现漏乘现象
(3)运算要有顺序:先乘方,再乘除,最后加减
(4)对于混合运算,注意最后应合并同类项
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
