1.4 整式的乘法(第3课时)教学课件 北师大版中学数学七年级(下)
文档属性
| 名称 | 1.4 整式的乘法(第3课时)教学课件 北师大版中学数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第 一章 整式的乘除
第一章 整式的乘除
1.4 整式的乘法
第3课时 多项式与多项式相乘
学 习 目 标
1.理解并经历探索多项式乘多项式法则的过程, 熟练应用多项式乘多项式的法则解决问题.(重点)
2.培养独立思考、主动探索的习惯和初步解决问
题的能力.
知识回顾
1.单项式与单项式相乘
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
2.单项式与多项式相乘
单项式与多项式相乘,就是根据乘法分配律用单项式去乘多项式的每一项,再把所得的积相加.
3.进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:即单项式要乘遍多项式的每一项
② 去括号时注意符号的确定.
计算:(-4x)·(2x2+3x-1);
新课导入
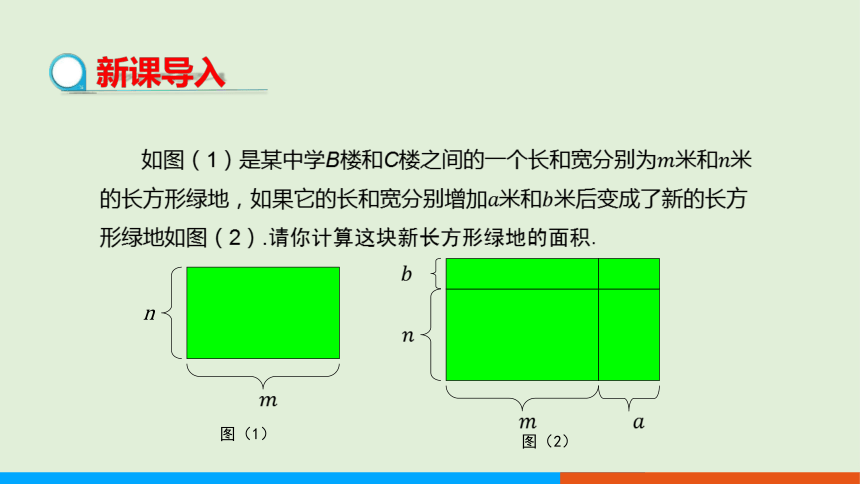
如图(1)是某中学B楼和C楼之间的一个长和宽分别为米和米的长方形绿地,如果它的长和宽分别增加米和米后变成了新的长方形绿地如图(2).请你计算这块新长方形绿地的面积.
n
图(1)
图(2)
知识讲解
新绿地面积:
方法1 =( ) ( )
方法3 =
你能用不同的方法来计算出新长方形绿地的面积吗?
方法2 =
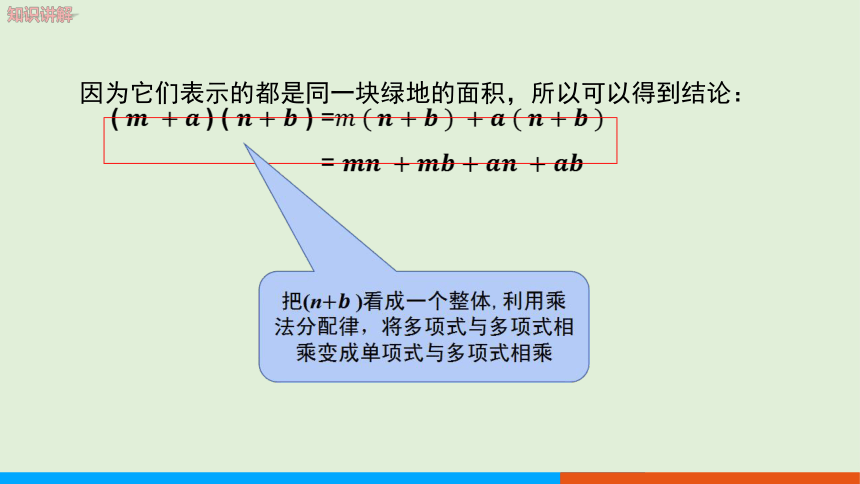
因为它们表示的都是同一块绿地的面积,所以可以得到结论:
( ) ( ) =
=
把(n)看成一个整体,利用乘法分配律,将多项式与多项式相乘变成单项式与多项式相乘
多项式与多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
()( )=
+
+
+
例1
(1) (+2)(5+3) ;
(2) (2 –3)(+4).
解:
(1)(+2 )(5 +3 )
=
=
(2)(2 –3)(+4)
2 2
+8
–3
–12
=2 2
+5
计算:
=
–12
·5
+
·3
+2
·5
+2
·3
5
+3
+10
+6
所得积的符号由这
两项的符号来确定:
负负得正
一正一负得负。
1. 两项相乘时,先定符号。
2.最后的结果要合并同类项.
1.运算要按一定顺序,做到不重不漏.
2.多项式乘多项式,积的项数应等于两个多项式的项数之积.
3.多项式的每一项分别与另一多项式的每一项相乘时,要带上每项前面的符号一起运算:同号相乘得正,异号相乘得负.
注意事项:
例2
计算:
解:原式
先化简,再求值:
,其中
,
解:
例3
例4
已知ax2+bx+1(a≠0)与3x-2的积不含x2项,
也不含x项,求系数a,b的值.
解: (ax2+bx+1)(3x-2)
=3ax3-2ax2+3bx2-2bx+3x-2
=3ax3+(-2a+3b)x2+(-2b+3)x-2.
∵积不含x2项,也不含x项,
计算:
(1)(x+2)(x+3)=__________;
(2)(x-4)(x+1)=__________;
(3)(y+4)(y-2)=__________;
(4)(y-5)(y-3)=__________.
x2+5x+6
x2-3x-4
y2+2y-8
y2-8y+15
由上面计算的结果找规律,观察填空:
(x+p)(x+q)=___2+______x+_______.
x
(p+q)
pq
拓展练习
随堂训练
1.下列多项式相乘,结果为x2-4x-12的是( )
A.(x-4)(x+3) B.(x-6)(x+2)
C.(x-4)(x-3) D.(x+6)(x-2)
2.如果(x+a)(x+b)的结果中不含x的一次项,那么a,b
满足 ( )
A.a=b B.a=0
C.a=-b D.b=0
B
C
3.计算:
(1)
(2)
(3)
(4)
解:原式
解:原式
解:原式
解:原式
解:原式
解:原式
4.化简求值:(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中 x=1,y=-2.
解:(4x+3y)(4x-3y)+(2x+y)(3x-5y)
当x=1,y=-2时,
原式=22×1-7×1×(-2)-14×(-2)2
=22+14 -56
=-20.
课堂小结
实质:转化为单项式乘多项式的运算
多项式与多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
()( )=
+
+
+
第 一章 整式的乘除
第一章 整式的乘除
1.4 整式的乘法
第3课时 多项式与多项式相乘
学 习 目 标
1.理解并经历探索多项式乘多项式法则的过程, 熟练应用多项式乘多项式的法则解决问题.(重点)
2.培养独立思考、主动探索的习惯和初步解决问
题的能力.
知识回顾
1.单项式与单项式相乘
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
2.单项式与多项式相乘
单项式与多项式相乘,就是根据乘法分配律用单项式去乘多项式的每一项,再把所得的积相加.
3.进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:即单项式要乘遍多项式的每一项
② 去括号时注意符号的确定.
计算:(-4x)·(2x2+3x-1);
新课导入
如图(1)是某中学B楼和C楼之间的一个长和宽分别为米和米的长方形绿地,如果它的长和宽分别增加米和米后变成了新的长方形绿地如图(2).请你计算这块新长方形绿地的面积.
n
图(1)
图(2)
知识讲解
新绿地面积:
方法1 =( ) ( )
方法3 =
你能用不同的方法来计算出新长方形绿地的面积吗?
方法2 =
因为它们表示的都是同一块绿地的面积,所以可以得到结论:
( ) ( ) =
=
把(n)看成一个整体,利用乘法分配律,将多项式与多项式相乘变成单项式与多项式相乘
多项式与多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
()( )=
+
+
+
例1
(1) (+2)(5+3) ;
(2) (2 –3)(+4).
解:
(1)(+2 )(5 +3 )
=
=
(2)(2 –3)(+4)
2 2
+8
–3
–12
=2 2
+5
计算:
=
–12
·5
+
·3
+2
·5
+2
·3
5
+3
+10
+6
所得积的符号由这
两项的符号来确定:
负负得正
一正一负得负。
1. 两项相乘时,先定符号。
2.最后的结果要合并同类项.
1.运算要按一定顺序,做到不重不漏.
2.多项式乘多项式,积的项数应等于两个多项式的项数之积.
3.多项式的每一项分别与另一多项式的每一项相乘时,要带上每项前面的符号一起运算:同号相乘得正,异号相乘得负.
注意事项:
例2
计算:
解:原式
先化简,再求值:
,其中
,
解:
例3
例4
已知ax2+bx+1(a≠0)与3x-2的积不含x2项,
也不含x项,求系数a,b的值.
解: (ax2+bx+1)(3x-2)
=3ax3-2ax2+3bx2-2bx+3x-2
=3ax3+(-2a+3b)x2+(-2b+3)x-2.
∵积不含x2项,也不含x项,
计算:
(1)(x+2)(x+3)=__________;
(2)(x-4)(x+1)=__________;
(3)(y+4)(y-2)=__________;
(4)(y-5)(y-3)=__________.
x2+5x+6
x2-3x-4
y2+2y-8
y2-8y+15
由上面计算的结果找规律,观察填空:
(x+p)(x+q)=___2+______x+_______.
x
(p+q)
pq
拓展练习
随堂训练
1.下列多项式相乘,结果为x2-4x-12的是( )
A.(x-4)(x+3) B.(x-6)(x+2)
C.(x-4)(x-3) D.(x+6)(x-2)
2.如果(x+a)(x+b)的结果中不含x的一次项,那么a,b
满足 ( )
A.a=b B.a=0
C.a=-b D.b=0
B
C
3.计算:
(1)
(2)
(3)
(4)
解:原式
解:原式
解:原式
解:原式
解:原式
解:原式
4.化简求值:(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中 x=1,y=-2.
解:(4x+3y)(4x-3y)+(2x+y)(3x-5y)
当x=1,y=-2时,
原式=22×1-7×1×(-2)-14×(-2)2
=22+14 -56
=-20.
课堂小结
实质:转化为单项式乘多项式的运算
多项式与多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
()( )=
+
+
+
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
