第十九章 平面直角坐标系 教学详案--冀教版数学八年级(下)
文档属性
| 名称 | 第十九章 平面直角坐标系 教学详案--冀教版数学八年级(下) |  | |
| 格式 | docx | ||
| 文件大小 | 14.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:23:49 | ||
图片预览


文档简介
第十九章 平面直角坐标系
19.1 确定平面上物体的位置
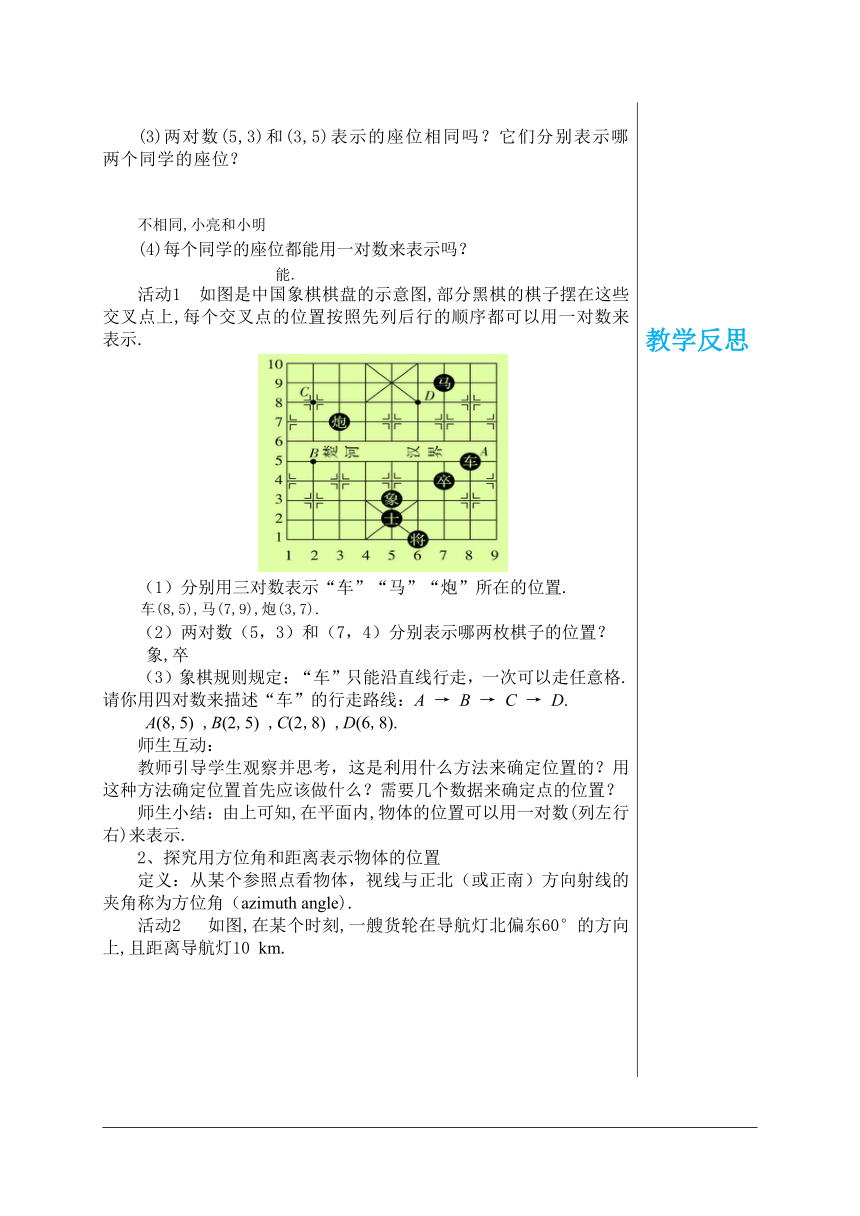
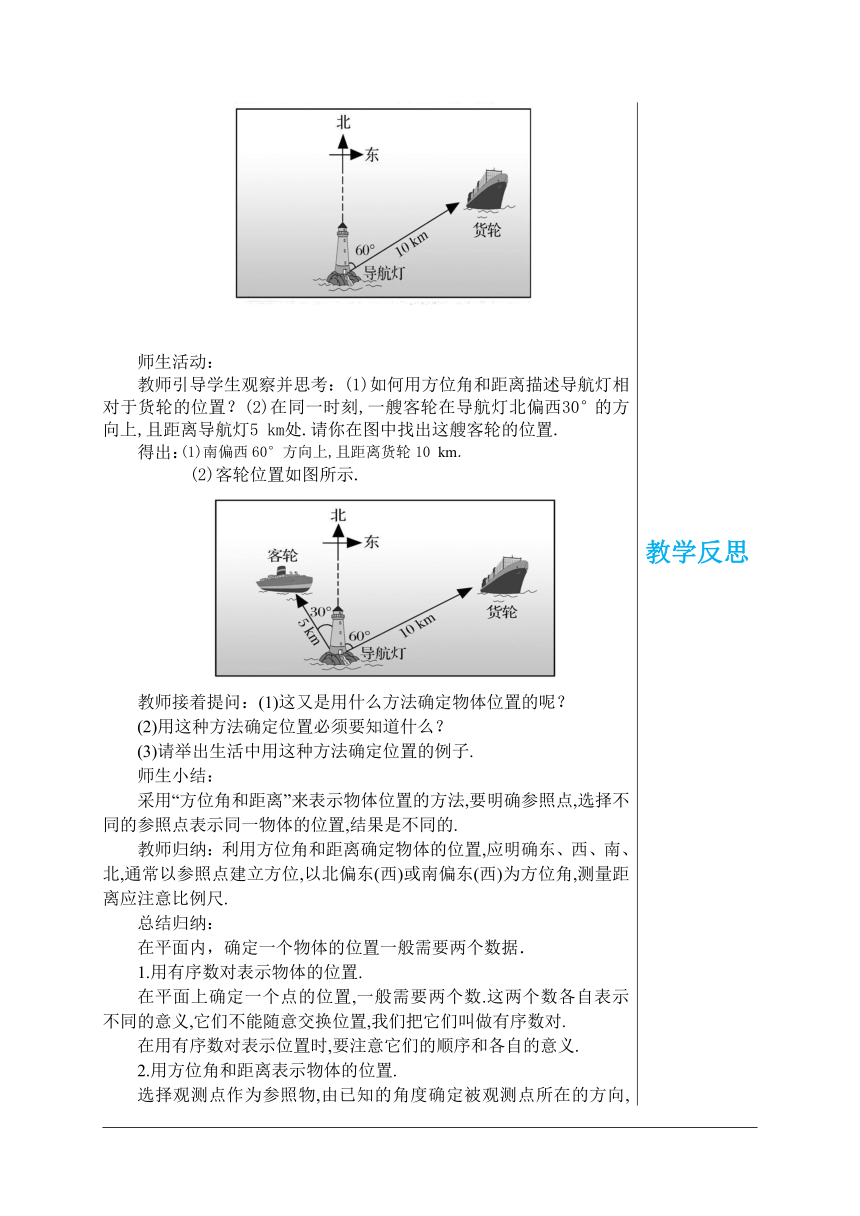
教学目标 1.探索确定平面上物体位置的方法. 2.会用“有序数对”“方位角和距离”表示平面上物体的位置. 教学重点难点 重点:探索确定平面上物体位置的方法. 难点:会用“有序数对”“方位角和距离”表示平面上物体的位置. 教学过程 导入新课 教师提问:在数轴上,如何确定一个点的位置呢? 例如: A点记作-2,B点记作3. 小结:在直线上一般用一个数据就可以表示一个点的位置. 探究新知 1、探究用有序数对表示物体位置 如图,每个同学在教室里都有一个确定的座位.按照列在前、行在后的顺序,每个座位都可以用一对数来表示.例如,在下面部分同学的座次表中,小明在第3列第5行,可以用一对数(3,5)来表示他的座位位置. 学生思考: 按照上面的表示方法,讨论下面的问题: (1)小强的座位应该用哪对数来表示?小亮和小红的座位呢? (2)一对数(1,4)表示的是哪个同学的座位? (3)两对数(5,3)和(3,5)表示的座位相同吗?它们分别表示哪两个同学的座位? (4)每个同学的座位都能用一对数来表示吗? 活动1 如图是中国象棋棋盘的示意图,部分黑棋的棋子摆在这些交叉点上,每个交叉点的位置按照先列后行的顺序都可以用一对数来表示. (1)分别用三对数表示“车”“马”“炮”所在的位置. (2)两对数(5,3)和(7,4)分别表示哪两枚棋子的位置? 象,卒 (3)象棋规则规定:“车”只能沿直线行走,一次可以走任意格.请你用四对数来描述“车”的行走路线:A → B → C → D. A(8,5) ,B(2,5) ,C(2,8) ,D(6,8). 师生互动: 教师引导学生观察并思考,这是利用什么方法来确定位置的?用这种方法确定位置首先应该做什么?需要几个数据来确定点的位置? 师生小结:由上可知,在平面内,物体的位置可以用一对数(列左行右)来表示. 2、探究用方位角和距离表示物体的位置 定义:从某个参照点看物体,视线与正北(或正南)方向射线的夹角称为方位角(azimuth angle). 活动2 如图,在某个时刻,一艘货轮在导航灯北偏东60°的方向上,且距离导航灯10 km. 师生活动: 教师引导学生观察并思考:(1)如何用方位角和距离描述导航灯相对于货轮的位置?(2)在同一时刻,一艘客轮在导航灯北偏西30°的方向上,且距离导航灯5 km处.请你在图中找出这艘客轮的位置. 得出: (2)客轮位置如图所示. 教师接着提问:(1)这又是用什么方法确定物体位置的呢? (2)用这种方法确定位置必须要知道什么? (3)请举出生活中用这种方法确定位置的例子. 师生小结: 采用“方位角和距离”来表示物体位置的方法,要明确参照点,选择不同的参照点表示同一物体的位置,结果是不同的. 教师归纳:利用方位角和距离确定物体的位置,应明确东、西、南、北,通常以参照点建立方位,以北偏东(西)或南偏东(西)为方位角,测量距离应注意比例尺. 总结归纳: 在平面内,确定一个物体的位置一般需要两个数据. 1.用有序数对表示物体的位置. 在平面上确定一个点的位置,一般需要两个数.这两个数各自表示不同的意义,它们不能随意交换位置,我们把它们叫做有序数对. 在用有序数对表示位置时,要注意它们的顺序和各自的意义. 2.用方位角和距离表示物体的位置. 选择观测点作为参照物,由已知的角度确定被观测点所在的方向,由距离确定被观测点的位置,这种方法在航海、航空和测量中经常用到. 课堂练习 1.在平面内,下列数据不能确定物体位置的是( ) A.3楼5号 B.北偏西40° C.解放路30号 D.东经120°,北纬30° 2.课间操时,小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( ) A.(5,4) B.(4,5) C.(3,4) D.(4,3) 3.如果座位表上“5列2行”记作(5,2),那么(4,3)表示 ( ) A.3列5行 B.5列3行 C.4列3行 D.3列4行 4.如图,如何描述小明家相对于学校的位置?学校相对于小明家的位置又该怎么描述? 5.如图,以学校为参照点,请用方位角和实际距离分别表示新华书店、少年宫和超市的位置. (图上1 cm代表实际500 m) 代 参考答案 1.B 2.D 3.C 4.解:小明家在学校北偏西50°的方向上,且距离学校500 m处. 学校在小明家南偏东50°的方向上,且距离小明家500 m处. 5.解:新华书店在学校北偏西40°的方向上,且距学校800 m处. 少年宫在学校南偏西20°的方向上,且距学校1 600 m处. 超市在学校北偏东60°的方向上,且距学1 100 m 处. 课堂小结 布置作业 教材第32页习题. 板书设计 第十九章 平面直角坐标系 19.1 确定平面上物体的位置 教学反思 教学反思 教学反思 教学反思 教学反思
第十九章 平面直角坐标系
19.2 平面直角坐标系
第1课时 平面直角坐标系
教学目标 1、理解平面直角坐标系以及横轴、纵轴、原点、坐标轴等概念. 2、能在给定的直角坐标系中,由点的位置写出它的坐标. 教学重难点 重点:理解平面直角坐标系以及横轴、纵轴、原点、坐标轴等概念. 难点:能在给定的直角坐标系中,由点的位置写出它的坐标. 教学过程 导入新课 回顾旧知: 我们已经学过了数轴,知道数轴上的点与实数一一对应,在建立了数轴之后,我们就可以确定直线上点的位置,如图. 学生思考: 点A代表的数字为( ﹣4 ) 点B代表的数字为( 2 ) -1所对应的点是( C ) 5所对应的点是( D ) 教师提问:那么,如何确定平面内点的位置呢? 引入新课:平面直角坐标系. 探究新知 如图是某城市部分街道的示意图.在繁星大道和中山路的交叉口点O处,小亮向交警叔叔问路. 提问:(1)按照交警的指示,小亮能找到图书大厦吗? (2)如果约定以点O处为参照点,先说出向东(或向西)方向上的距离,再说向北(或向南)方向上的距离,那么图书大厦附近交叉路口P点可以怎样表示? 学生思考后回答:(1)能;(2)P(东3 km,北2 km). 如果我们把中山路看成一条数轴(向东的方向为正),把繁星大道看成另一条数轴(向北的方向为正),把它们的交点O看成两条数轴的公共原点,以1 km作为数轴的单位长度,那么点P的位置就可以用一对数(3,2)来表示. 学生接着观察图片,并思考下列问题: (1)点A,B,C的位置应如何表示? (2)你能在图中找到用(3,-1.5),(-2,2)表示的点的位置吗? (3)街道所在平面上的任何一点,它的位置都可以用一对数表示出来吗?举例说明. 学生独立思考,动手操作. 探究1 平面直角坐标系 教师引导学生探究平面直角坐标系的定义. 学生动手操作: 指出点B的坐标,记作B(-4,1). 通过学习点A坐标的确认方法,并让学生说M,N,P,Q的坐标. 点M坐标为(3.5,2);点N坐标为(-4,3); 点P坐标为(-3,-2); 点Q坐标为(4,-2). 通过上面的练习,师生共同总结出确定点的位置的方法. 想一想: 知道了点的坐标,如何确定点的位置呢? 在平面直角坐标系中找到点A(3,-2). 教师指导学生完成例1的学习. 例1 如图,在平面直角坐标系中,描出点A(0,4),B(4,2),C(2,-3),D(-2,-3),E(-4,2),并依次连接ABCDEA. 解:在y轴上描出表示4的点,即得A(0,4).分别过x轴上表示4的点和y轴上表示2的点,作x轴和y轴的垂线,两条垂线的交点就是点B(4,2). 同理,可以描出C,D,E三点. 依次连接ABCDEA,得到图中所示的图形. 教师小结:实数与数轴上的点具有一一对应关系,由此可知,坐标平面上的点与有序实数对具有一一对应关系,即坐标平面上任意一点都可以用唯一一对有序实数来表示;反过来,任意一对有序实数都可以表示坐标平面上唯一一个点. 课堂练习 1.如图所示,这是某城市部分简图,每个小正方形的边长为1个单位长度,以火车站所在的位置为坐标原点建立平面直角坐标系,并分别写出各场所的坐标. 2.如图所示,这是某城市部分简图,每个小正方形的边长为1个单位长度,以火车站所在的位置为坐标原点建立平面直角坐标系,并分别写出各场所的坐标. 3.如图,点A的坐标为( ) A.(-2,3) B.(2,-3) C.(-2,-3) D.(2,3) 4.如图,点A的坐标为 ,点B的坐标为 . 5.在直角坐标系中描出下列各点: A(4,3),B(-2,3),C(-4,-1),D(2,-2). 参考答案 1.解:如图所示,建立平面直角坐标系,可得医院的坐标为(-2,-2),文化馆的坐标为(-3,1),体育场的坐标为(-4,3),宾馆的坐标为(2,2),市场的坐标为(4,3),超市的坐标为(2,-3). 2.解:如图所示,建立平面直角坐标系,可得医院的坐标为(-1,0),文化馆的坐标为(-2,3), 体育场的坐标为(-3,5),宾馆的坐标为(3,4),市场的坐标为(5,5), 超市的坐标为(3,-1). 3.A 4.(-2,0) (0,-2) 5. S 课堂小结 布置作业 教材第37页习题A组第1,3题. 板书设计 第十九章 平面直角坐标系 19.2 平面直角坐标系 平面直角坐标系 教学反思 教学反思 教学反思 教学反思 教学反思 教学反思
第十九章 平面直角坐标系
19.2 平面直角坐标系
第2课时 平面直角坐标系中点的坐标特征
教学目标 1.掌握平面直角坐标系中各象限、坐标轴上点的坐标特征. 2.掌握点关于坐标轴及原点的对称点的坐标特征. 教学重点难点 重点:掌握平面直角坐标系中各象限、坐标轴上点的坐标特征. 难点:掌握点关于坐标轴及原点的对称点的坐标特征. 教学过程 导入新课 回顾旧知: 我们知道了可以用有序实数对来表示平面上点的位置.而在实际应用中,我们往往要先建立平面直角坐标系. 在平面内,画两条有公共原点且互相垂直的数轴,就构成了平面直角坐标系,简称直角坐标系.水平方向的数轴叫做x轴(或横轴),取向右为正方向;竖直方向叫做y轴(或纵轴),取向上为正方向.x轴与y轴的公共原点叫做坐标原点. 两条数轴统称为坐标轴. 回忆上节课所学的知识,加深学生对定义的理解,从而引出本节课的内容. 探究新知 注意:1.数字必须是中文大写一、二、三、四. 2.坐标轴上的点不属于任何一个象限. 如图,平面直角坐标系的两条坐标轴将平面分成了四部分,从右上角的部分说起,按逆时针方向,各部分依次叫做第一象限、第二象限、第三象限和第四象限. 选出一名同学上黑板任画一平面直角坐标系,然后说明第一象限、第二象限、第三象限、第四象限的位置.明确坐标轴上的点不属于任何象限. 探究1 象限内、坐标轴上点的特征 如图所示,八边形ABCDEFGH与两条坐标轴的交点分别是M,N,P,Q四点. 学生分组讨论: (1)分别写出图中各点的坐标. (2)观察各点坐标,你认为同一象限内点的坐标的共同特点是什么? (3)指出坐标轴上点的坐标的共同特点. 学生观察图形,分析问题,互相交流. 学生回答后,小结: 1.A(3,1),B(1,3),C(-1,3),D(-3,1),E(-3,-1),F(-1,-3),G(1,-3) , H(3,-1),P(0,3),Q(0,-3), M(3,0),N(-3,0). 2.同一象限内点的横、纵坐标符号分别相同. 3.x轴上的点的纵坐标都是0,y轴上的点的横坐标都是0. 练一练:分别说出下列各点在哪个象限内或在哪条坐标轴上? A(6,-2),B(0,3),C(3,7),D(-6,-3),E(-2,0),F(-9,5). 思考:任一点P(x,y). (1)如果P(x,y)在第二象限,那么x,y分别是正数还是负数? (2)如果x>0,y<0,P(x,y)在第几象限? 引导学生思考上面的问题,总结出四个象限内点的坐标的特征,并画出下面帮助学生记忆. 分析总结:第一、二、三、四象限内点的坐标的符号分别是 (+,+), (-,+) , (-,-), (+,-). 探究2 关于x轴,y轴和原点对称的点的特征 如图所示,八边形ABCDEFGH与两条坐标轴的交点分别是M,N,P,Q四点. 点B关于x轴的对称点是G(1,-3); 点B关于y轴的对称点是C(-1,3); 点B关于原点的对称点是F(-1,-3). 观察图片,讨论:分别写出点B(1,3)关于x轴的对称点坐标,关于y轴的对称点坐标,关于原点的对称点坐标.关于x轴,y轴和原点的对称点的特征分别是什么? 共同归纳: (1)关于x轴对称的两点横坐标相同,纵坐标互为相反数; (2)关于y轴对称的两点横坐标互为相反数,纵坐标相同; (3)关于原点对称的两点横、纵坐标都互为相反数. 出示例2:建立直角坐标系,并解决下列问题. (1)描出下列各点,并把各点依次连接成封闭图形. A(1,-1),B(3,-1),C(3,1),D(1,1),E(1,3),F(-1,3),G(-1,1),H(-3,1), I(-3,-1),J(-1,-1),K(-1,-3),L(1,-3). (2)观察所得的图形,它是轴对称图形吗?如果是轴对称图形,画出它的对称轴. (3)在画出的图形中,分别写出关于x轴,y轴和原点的对称点. 解:(1)描点,连线后得到的图形如图所示. (2)这个图形是轴对称图形,它有四条对称轴:x轴,y轴,l1,l2. (3)关于x轴的对称点分别是点A和点D,点B和点C,点E和点L,点F和点K,点G和点J,点H和点I.关于y轴的对称点分别是点A和点J,点B和点I,点C和点H,点D和点G,点E和点F,点L和点K.关于原点的对称点分别是点A和点G,点B和点H,点C和点I,点D和点J,点E和点K,点F和点L. 说明:描点的过程中,教师要巡视指导,发现错误及时纠正. 师生共同总结:平面直角坐标系中相关点的坐标的特征 (1)在平面直角坐标系中,x轴和y轴将平面分成四个部分,按逆时针方向依次叫做第一象限、第二象限、第三象限、第四象限.坐标轴上的点不属于任何一个象限. (2)各象限内点的坐标有以下特征:如果点A(x,y)在第一象限,那么x>0,y>0;如果点A(x,y)在第二象限,那么x<0,y>0;如果点A(x,y)在第三象限,那么x<0,y<0;如果点A(x,y)在第四象限,那么x>0,y<0. (3)如果点A(x,y)在x轴上,那么y=0,x为任意实数;如果点A(x,y)在y轴上,那么x=0,y为任意实数;如果点A(x,y)既在x轴上又在y轴上,那么x=0且y=0. (4)平面直角坐标系中的点P(x,y),关于x轴对称点的坐标为(x,-y),关于y轴对称点的坐标为(-x,y),关于原点对称点的坐标为(-x,-y). 师生继续探讨: 相互交流,共同探讨: 点M(-3,4)到x轴、y轴和坐标原点的距离分别多少? MN=4,MH=3,MO=5. 小结: 总结规律 ①点P(a,b)到x轴的距离是|b|; ②点P(a,b)到y轴的距离是|a|; ③点P(a,b)到原点的距离是. 课堂练习 1.在平面直角坐标系中,点(1,5)所在的象限是 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.已知点P(0,a)在y轴的负半轴上,则点Q(-a2-1,-a+1)在 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 4.如图所示,点A(-2,1)到y轴的距离为( ) A.-2 B.1 C.2 D. 5.如图所示,下列各点在阴影区域内的是( ) A.(3,2) B.(-3,2) C.(3,-2) D.(-3,-2) 6.若点P(2k-1,1-k)在第四象限,则k的取值范围为( ) A.k>1 B.k< C.k> D.第十九章 平面直角坐标系
19.3 坐标与图形的位置
教学目标 1.能建立适当的直角坐标系,描述图形的位置. 2.通过用直角坐标系表示图形的位置,使学生体会平面直角坐标系在实际问题中的应用. 教学重点难点 重点:能建立适当的直角坐标系,描述图形的位置. 难点:通过用直角坐标系表示图形的位置,使学生体会平面直角坐标系在实际问题中的应用. 教学过程 导入新课 复旧引新: 利用平面直角坐标系的知识,用坐标表示各个景点的位置: 想一想:同一个点在不同的坐标系中,坐标相同吗? 教师引导学生得出:同一个点在不同的坐标系中,坐标不相同. 2.利用平面直角坐标系的知识,说出下面各点的坐标. 通过复习有利于本节内容的学习,为下面内容的继续做好铺垫. 探究新知 小亮想把下面的四边形的形状通过电话告诉小强,让小强也能准确地画出相同的图形.他们该怎么做呢? 有人说:“建立个平面直角坐标系,告诉这个四边形四个顶点的坐标就能画出相同的图形”. 你认为这种说法可行吗?大家动手画一画吧. 在实际生活中,经常需要建立适当的直角坐标系,通过坐标来描述某个图形的位置与形状. 揭示课题:坐标与图形的位置. 大家思考一下: 直角坐标系建立的不同,点的坐标会怎么样呢? 活动1 已知一个边长是4的正方形.建立适当的直角坐标系,通过各顶点的坐标来描述它的位置. 学生小组内交流,得出: 解:如图,以顶点B为原点,BC所在直线为x轴,AB所在直线为y轴建立平面直角坐标系. 正方形四个顶点A,B,C,D的坐标分别为 A(0,4), B(0,0),C(4,0), D(4,4). 活动2 解:以正方形对角线的交点为原点,水平方向直线为x轴,竖直方向直线为y轴建立平面直角坐标系. 正方形四个顶点A,B,C,D的坐标分别为 A(-2,2),B(-2,-2),C(2, -2),D(2,2). 活动3 解:以正方形对角线的交点为原点,BD所在直线为x轴,AC所在直线为y轴建立平面直角坐标系. 正方形四个顶点A,B,C,D的坐标分别为 小组内先独立思考后,发表自己不同的看法,画图操作,并表示出顶点的坐标. 直角坐标系点A坐标点B坐标点C坐标点D坐标活动1(0,4)(0,0)(4,0)(4,4)活动2(-2,2)(-2,-2)(2,-2)(2,2)活动3
想一想:这三种建立直角坐标系的方式各有什么优点?说明你的理由. 学生得出:这样建立直角坐标系会很方便的表示出点的坐标,便于观察和计算. 小结:建立不同的直角坐标系,同一个图形的顶点坐标也不同,应根据具体情况建立适当的直角坐标系. 注意: (1)建立直角坐标系的方法有很多,由于坐标系的选择直接影响计算的繁简程度,所以建立直角坐标系时,要以能简捷地确定平面内点的坐标为原则. (2)建立新的直角坐标系确定几何图形上点的坐标,应充分考虑到易于求点到坐标轴的距离.否则,计算麻烦,有时根本无法确定这些点的坐标. 练一练: 如图所示,在等腰三角形ABC中,底边BC=4,高AD=6. (1)请你建立适当的直角坐标系,并写出点A,B,C的坐标. (2)说明你选择这个直角坐标系的理由. 学生思考后得出:(1)以线段BC所在直线为x轴,线段DA所在直线为y轴,建立直角坐标系,则A(0,6),B(-2,0),C(2,0). (2)理由:这样建立的平面直角坐标系,能保证等腰三角形的顶点都在坐标轴上,便于书写出顶点的坐标. 教师指明:体现了轴对称性. 另一名同学思考后,得出:以B为坐标原点,BC所在直线为x轴,过点B且垂直于BC的直线为y轴建立平面直角坐标系. A(2,6),B (0,0), C (4,0). 学生们各抒已见,发表自己的看法. 议一议:建立坐标系常用的方法有哪些? 小结: 课堂练习 1.一个长方形在平面直角坐标系中,它的三个顶点的坐标分别为(-3,-1),(2,-1),(2,2),则第四个顶点的坐标为( ) A.(-3,2) B.(3,2) C.(-3,-4) D.(7,2) 2.如图所示,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为( ) A.(3,1) B.(-1,1) C.(3,5) D.(-1,5) 3.如图所示,将长为3 cm的长方形ABCD放在平面直角坐标系中,若点D(6,3),则A点的坐标为( ) A.(5,3) B.(4,3) C.(4,2) D.(3,3) 4.如图所示,正方形ABCD中点A和点C的坐标分别为(-2,3)和(3,-2),则点B和点D的坐标分别为( ) A.(2,2)和(3,3) B.(-2,-2)和(3,3) C.(-2,-2)和(-3,-3) D.(2,2)和(-3,-3) 5.如图所示,长方形ABCD中,AB=3,BC=4,且点A在坐标原点,则C点的坐标为( ) A.C(4,3) B.C(4,-3) C.C(3,-4) D.C(-4,-3) 6.一个直角三角形ABC的两条直角边为3和4,现在把它放在不同的坐标系中,请写出各顶点的坐标. 参考答案 1.A 2.C 3.D 4.B 5.B 6. 课堂小结 布置作业 教材第43页习题A组第1,2 题. 板书设计 第十九章 平面直角坐标系 19.3 坐标与图形的位置 教学反思 教学反思 教学反思 教学反思 教学反思 教学反思
第十九章 平面直角坐标系
19.4 坐标与图形的变化
第1课时 图形的平移与坐标变化
教学目标 1、掌握点平移得到新坐标的规律,并且熟练画出图形. 2、理解“数形结合”,体会坐标系中图形平移的实际应用. 教学重难点 重点:掌握点平移得到新坐标的规律,并且熟练画出图形. 难点:理解“数形结合”,体会坐标系中图形平移的实际应用. 教学过程 导入新课 教师提问: 1、你还记得什么叫平移吗? 在平面内,把一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移. 2、图形平移的性质是什么? (1)新图形与原图形形状和大小不变,但位置改变; (2)对应点的连线平行且相等. 课前小练 如图所示,长方形公园ABCD的长、宽分别是6千米、4千米,以公园中心O为原点建立直角坐标系,写出各顶点的坐标. A(3,2),B(-3,2),C(-3,-2),D(3,-2). 【学生思考】 (1)观察上图,由点B到点A是怎样移动的?(点B向右移动6个单位长度得到点A) (2)在图中,你还能看到由一点怎样移动得到另一点? 探究新知 1、探究坐标系中点的平移 活动1 根据上图回答问题: 将点A(-2,-3)向右平移5个单位长度,得到点A1( 3 , -3); (2)将点A(-2,-3)向左平移2个单位长度,得到点A2(-4 , -3); (3)将点A(-2,-3)向上平移4个单位长度,得到点A3(-2 , 1 ) ; (4)将点A(-2,-3)向下平移2个单位长度,得到点A4(-2 , -5 ). 师生互动: 教师引导学生观察并思考,点A左右平移时哪个坐标发生变化,是如何变化的? 当点A上下平移时那个坐标发生变化,是如何变化的? 活动2 在坐标平面上,一只蚂蚁从原点出发,爬行的路径如图所示. 写出A,B,C,D,E这五个点的坐标. A(0,2),B(3,2),C(3,-2),D(-3,-2),E(-3,3). (2)指出蚂蚁在各条线段上爬行的方向和距离,并填写下表. 移动的路径平移的方向和距离坐标的变化横坐标纵坐标O(0,0)→A(0,2)向上平移2个单位长度不变加2A(0,2)→B(3,2)向右平移3个单位长度加3不变B(3,2)→C(3,-2)向下平移4个单位长度不变减4C(3,-2)→D(-3,-2)向左平移6个单位长度减6不变D(-3,-2)→E(-3,3)向上平移5个单位长度不变加5
(3)观察各点的坐标变化,当P(x,y)沿x轴左右平移时坐标有什么变化?当点P(x,y)沿y轴上下平移时坐标有什么变化? 师生总结: 点沿x轴平移时,纵坐标不变,横坐标左减右加;点沿y轴平移时,横坐标不变,纵坐标上加下减. 探究坐标中图形的平移 例:如图所示,在平面直角坐标系中,长方形ABCD各顶点的坐标分别为A(-2,1),B(2,1),C(2,3),D(-2,3).将长方形ABCD沿x轴的方向向右平移5个单位长度,得到长方形A1B1C1D1.请写出长方形A1B1C1D1各顶点的坐标,并指出对应顶点坐标的变化规律. 学生活动 自主完成.将长方形ABCD沿x轴的方向向右平移5个单位长度,各顶点移动的方向一致,移动的距离都是5个单位长度.因此,平移后的长方形A1B1C1D1各顶点的坐标为A1(3,1),B1(7,1),C1(7,3),D1(3,3). 观察与思考: 图形的平移可以转化为哪几个点的平移? (2)这几个点的平移是否一致? (3)在平移中,各点的坐标分别发生了怎样的变化? 师生总结: 顶点坐标的变化规律为:长方形A1B1C1D1各顶点的横坐标是将长方形ABCD各顶点的横坐标都增加5,纵坐标不变而得到的. 3、深化理解,总结规律 在例题的图中,将长方形ABCD沿y轴的方向向下平移4个单位长度,画出平移后的长方形,写出各顶点的坐标,并说出图形平移前后对应顶点的坐标是如何变化的. A(-2,1)→A1(-2,-3), B(2,1)→B1(2,-3), C(2,3)→C1(2,-1), D(-2,3)→D1(-2,-1). 总结规律:平移后的长方形各顶点纵坐标是由长方形ABCD各顶点的纵坐标都减少4,横坐标不变得到的. 2.若将长方形ABCD先沿x轴的方向向右平移6个单位长度,再沿y轴的方向向下平移5个单位长度,画出平移后的长方形,写出其各顶点的坐标,并说出图形平移前后对应顶点的坐标是如何变化的. A(-2,1)→A2(4,-4), B(2,1)→B2(8,-4), C(2,3)→C2(8,-2), D(-2,3)→D2(4,-2). 总结规律:平移后的长方形各顶点横坐标是由长方形ABCD各顶点横坐标增加6,纵坐标是由其纵坐标减少5得到的. 教师提问: 一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系? 师生总结: (1)直角坐标系中,沿横轴平移,图形上每一点的纵坐标不变,而横坐标增减,简记“左减右加”;沿纵轴平移,横坐标不变,纵坐标增减,简记“上加下减”.“左减右加,上加下减”也可这样理解:沿x轴(y轴)正方向平移,则横(纵)坐标加上平移的单位数量,沿x轴(y轴)负方向平移,则横(纵)坐标减去平移的单位数量即可. (2) ①原图形向左(右)平移k个单位长度(k>0): 原图形上的点P(x,y)P1(x+k,y); 原图形上的点P(x,y)P2(x-k,y); ②原图形向上(下)平移k个单位长度(k>0): 原图形上的点P(x,y)P3(x,y+k); 原图形上的点P(x,y)P4(x,y-k). (3)在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数k,得到的新图形就是把原图形向右(或向左)平移k个单位长度;如果把一个图形各个点的纵坐标都加(或减去)一个正数k,得到的新图形就是把原图形向上(或向下)平移k个单位长度. 课堂练习 1.如图所示,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为 ( ) A.(2,-1) B.(2,3) C.(0,1) D.(4,1) 2.如图所示,把线段AB平移,使得点A到达点C(4,2),点B到达点D,那么点D的坐标是 ( ) A.(7,3) B.(6,4) C.(7,4) D.(8,4) 3.将点M(-1,-5)向右平移3个单位长度得到点N,则点N所在的象限是 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 4.如图所示,A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为 ( ) A.2 B.3 C.4 D.5 5.在平面直角坐标系中,将三角形各点的横坐标都减去3,纵坐标保持不变,所得图形与原图形相比 ( ) A.向右平移了3个单位 B.向左平移了3个单位 C.向上平移了3个单位 D.向下平移了3个单位 参考答案 1.A 2.C 3.D 4.A 5.B 课堂小结 布置作业 教材第46页习题A组第2,3题. 板书设计 第十九章 平面直角坐标系 19.4 坐标与图形的变化 第1课时 图形的平移与坐标变化 教学反思 教学反思 教学反思 教学反思 教学反思 教学反思
第十九章 平面直角坐标系
19.4 坐标与图形的变化
第2课时 图形的轴对称、放缩与坐标变化
教学目标 1、在同一直角坐标系内,感受坐标变化而使图形对称、扩大和缩小的过程,并能得出图形对称、扩大和缩小的规律. 2、通过探索图形上点的坐标变化与图形变换之间的关系,进一步体会数形结合的数学思想. 教学重难点 重难点:在同一直角坐标系内,感受坐标变化而使图形对称、扩大和缩小的过程,并能得出图形对称、扩大和缩小的规律. 教学过程 导入新课 出示问题,回忆旧知 什么叫轴对称图形? 沿着某一直线对折,直线两旁的部分能够完全重合的图形就是轴对称图形,这条直线称为对称轴. 学生活动: 1、动手画一画:已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗? 2、画出这些点分别关于x轴、y轴对称的点,并填写表格. 已知点A(2,-3)B(-1,2)C(-6,-5)D(3,5)E(4,0)F(0,-3)关于x轴的对称点(2,3)(-1,-2)(-6,5)(3,-5)(4,0)(0,3)关于y轴的对称轴(-2,-3)(1,2)(6,-5)(-3,5)(-4,0)(0,-3)
观察并思考:关于坐标轴对称的两个点的坐标有什么变化规律? 这样引导学生回忆轴对称图形的相关知识,并进行点的对称方面的作图与练习,为本节课知识的学习的打下了良好基础. 探究新知 1.探究成轴对称的两个图形的坐标变化 如图所示,在平面直角坐标系中,△ABC各顶点的坐标分别为: A(-5,1),B(-1,1),C(-2,4). 学生活动: (1)分别把点A,B,C关于x轴和y轴的对称点的坐标填写在下表中. (2)将A1,B1,C1连接起来,观察△A1B1C1与△ABC有什么位置关系? (3)将A2,B2,C2连接起来,观察△A2B2C2与△ABC有什么位置关系? (4)总结关于x轴成轴对称的两个图形的对应点的坐标之间有什么关系?关于y轴成轴对称时呢? △ABC顶点坐标A(-5,1)B(-1,1)C(-2,4)关于x轴的对称点A1(-5,-1)B1(-1,-1)C1(-2,-4)关于y轴的对称点A2(5,1)B2(1,1)C2(2,4)
总结: 关于x轴成轴对称的两个图形,各对应顶点的横坐标相等,纵坐标互为相反数; 关于y轴成轴对称的两个图形,各对应顶点的横坐标互为相反数,纵坐标相等. 学生活动:练一练 如图,左右两幅图案关于y轴对称,右侧图案中的左右眼睛的坐标分别是(2,3),(4,3).嘴角左右端点的坐标分别是(2,1),(4,1). 试确定左侧图案中的左右眼睛和嘴角左右端点的坐标. 答:左侧图案中的左眼坐标为(-4,3),右眼坐标为(-2,3),嘴角的左端点坐标为(-4,1),右端点坐标为(-2,1). 探究图形放缩的坐标变化 活动1: 如图所示,在直角坐标系中,五边形OABCD各顶点的坐标分别为: O(0,0),A(0,2),B(2,3),C(4,2),D(3,0). (1)将各顶点的横坐标和纵坐标都乘2,写出各对应点的坐标. O(0,0), A1(0,4), B1 (4,6),C1(8,4), D1(6,0). (2)在直角坐标系中,描出各点,然后依次连接,画出五边形OA1B1C1D1. O(0,0), A1 (0,4), B1 (4,6), C1 (8,4), D1 (6,0). (3)思考:两个五边形的形状、大小有什么变化? 形状没有发生变化,各边的长度变为原来的2倍,并且对应顶点的连线所在的直线都相交于一点. 活动2: 如图所示,说出O,A,B,C各点的坐标. O(0, 0),A (2, 6) ,B(6, 6) ,C(8,0). (2)把各顶点的横坐标和纵坐标都乘,分别写出各顶点坐标.然后画出图形,观察得到的图形与原图形的形状和大小的变化规律. O(0, 0) ,A1(1,3) ,B1(3,3) ,C1(4, 0). 形状没有发生变化,各边的长度变为原来的,且对应顶点的连线所在的直线都相交于一点. (3)观察并思考:将一个图形各顶点的横坐标和纵坐标都乘k,图形的形状和大小有什么变化? 师生总结: 将一个图形各顶点的横坐标和纵坐标都将一个图形各顶点的横坐标和纵坐标都乘k,所得图形的形状不变,各边扩大到原来的k倍且连接各对应顶点的直线相交于一点. 课堂练习 1.平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( ) A.y轴对称 B.x轴对称 C.原点对称 D.直线y=x对称 2.在平面直角坐标系中,将点A(-1,2)向右平移3个单位长度得到点B,则点B关于x轴的对称点C的坐标是( ) A.(-4,-2) B.(2,2) C.(-2,2) D.(2,-2) 3.如图所示,△ABC的顶点都在正方形网格格点上,点A的坐标为(-1,4).将△ABC沿y轴翻折到第一象限得到△A′B′C′,则点C的对应点C′的坐标是( ) A.(3,1) B.(-3,-1) C.(1,-3) D.(3,-1) 4.在平面直角坐标系中,等边三角形OAB关于x轴对称的图形是等边三角形OA′B′.若已知点A的坐标为(6,0),则点B′的横坐标是 ( ) A.6 B.-6 C.3 D.-3 5.在平面直角坐标系中,△ABC的位置如图所示,点A的坐标为(1,3),将△ABC先向左平移3个单位,再作出其关于x轴的对称图形,则A点的对应点的坐标为 ( ) A.(-3,-2) B.(-1,-2) C.(-2,-2) D.(-2,-3) 6.如图所示,△ABO缩小后变为△A′B′O,其中A,B的对应点分别为A′,B′,点A,B,A′,B′均在图中格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( ) A. B.( m,n) C. D. 7.在平面直角坐标系中,规定把一个正方形先沿着x轴翻折,再向右平移2个单位长度称为1次变换.如图,已知正方形ABCD的顶点A,B的坐标分别是(-1,-1)、(-3,-1),把正方形ABCD经过连续7次这样的变换得到正方形A′B′C′D′,求B的对应点B′的坐标. 参考答案 1.B 2.D 3.A 4.C 5.D 6.D 7.解:∵ 正方形ABCD,点A,B的坐标分别是(-1,-1)、(-3,-1), 根据题意,得第1次变换后的点B的对应点的坐标为(-3+2,1),即(-1,1), 第2次变换后的点B的对应点的坐标为(-1+2,-1),即(1,-1), 第3次变换后的点B的对应点的坐标为(1+2,1),即(3,1),…, 第n次变换后的点B的对应点的为:当n为奇数时为(2n-3,1),当n为偶数时为(2n-3,-1), ∴ 把正方形ABCD经过连续7次这样的变换得到正方形A′B′C′D′,则点B的对应点B′的坐标是(11,1). 课堂小结 布置作业 教材第61页习题A组第1,2题. 板书设计 第十九章 平面直角坐标系 19.4 坐标与图形的变化 第2课时 图形的轴对称、放缩与坐标变化 教学反思 教学反思 。 教学反思 教学反思 教学反思 教学反思 教学反思
19.1 确定平面上物体的位置
教学目标 1.探索确定平面上物体位置的方法. 2.会用“有序数对”“方位角和距离”表示平面上物体的位置. 教学重点难点 重点:探索确定平面上物体位置的方法. 难点:会用“有序数对”“方位角和距离”表示平面上物体的位置. 教学过程 导入新课 教师提问:在数轴上,如何确定一个点的位置呢? 例如: A点记作-2,B点记作3. 小结:在直线上一般用一个数据就可以表示一个点的位置. 探究新知 1、探究用有序数对表示物体位置 如图,每个同学在教室里都有一个确定的座位.按照列在前、行在后的顺序,每个座位都可以用一对数来表示.例如,在下面部分同学的座次表中,小明在第3列第5行,可以用一对数(3,5)来表示他的座位位置. 学生思考: 按照上面的表示方法,讨论下面的问题: (1)小强的座位应该用哪对数来表示?小亮和小红的座位呢? (2)一对数(1,4)表示的是哪个同学的座位? (3)两对数(5,3)和(3,5)表示的座位相同吗?它们分别表示哪两个同学的座位? (4)每个同学的座位都能用一对数来表示吗? 活动1 如图是中国象棋棋盘的示意图,部分黑棋的棋子摆在这些交叉点上,每个交叉点的位置按照先列后行的顺序都可以用一对数来表示. (1)分别用三对数表示“车”“马”“炮”所在的位置. (2)两对数(5,3)和(7,4)分别表示哪两枚棋子的位置? 象,卒 (3)象棋规则规定:“车”只能沿直线行走,一次可以走任意格.请你用四对数来描述“车”的行走路线:A → B → C → D. A(8,5) ,B(2,5) ,C(2,8) ,D(6,8). 师生互动: 教师引导学生观察并思考,这是利用什么方法来确定位置的?用这种方法确定位置首先应该做什么?需要几个数据来确定点的位置? 师生小结:由上可知,在平面内,物体的位置可以用一对数(列左行右)来表示. 2、探究用方位角和距离表示物体的位置 定义:从某个参照点看物体,视线与正北(或正南)方向射线的夹角称为方位角(azimuth angle). 活动2 如图,在某个时刻,一艘货轮在导航灯北偏东60°的方向上,且距离导航灯10 km. 师生活动: 教师引导学生观察并思考:(1)如何用方位角和距离描述导航灯相对于货轮的位置?(2)在同一时刻,一艘客轮在导航灯北偏西30°的方向上,且距离导航灯5 km处.请你在图中找出这艘客轮的位置. 得出: (2)客轮位置如图所示. 教师接着提问:(1)这又是用什么方法确定物体位置的呢? (2)用这种方法确定位置必须要知道什么? (3)请举出生活中用这种方法确定位置的例子. 师生小结: 采用“方位角和距离”来表示物体位置的方法,要明确参照点,选择不同的参照点表示同一物体的位置,结果是不同的. 教师归纳:利用方位角和距离确定物体的位置,应明确东、西、南、北,通常以参照点建立方位,以北偏东(西)或南偏东(西)为方位角,测量距离应注意比例尺. 总结归纳: 在平面内,确定一个物体的位置一般需要两个数据. 1.用有序数对表示物体的位置. 在平面上确定一个点的位置,一般需要两个数.这两个数各自表示不同的意义,它们不能随意交换位置,我们把它们叫做有序数对. 在用有序数对表示位置时,要注意它们的顺序和各自的意义. 2.用方位角和距离表示物体的位置. 选择观测点作为参照物,由已知的角度确定被观测点所在的方向,由距离确定被观测点的位置,这种方法在航海、航空和测量中经常用到. 课堂练习 1.在平面内,下列数据不能确定物体位置的是( ) A.3楼5号 B.北偏西40° C.解放路30号 D.东经120°,北纬30° 2.课间操时,小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( ) A.(5,4) B.(4,5) C.(3,4) D.(4,3) 3.如果座位表上“5列2行”记作(5,2),那么(4,3)表示 ( ) A.3列5行 B.5列3行 C.4列3行 D.3列4行 4.如图,如何描述小明家相对于学校的位置?学校相对于小明家的位置又该怎么描述? 5.如图,以学校为参照点,请用方位角和实际距离分别表示新华书店、少年宫和超市的位置. (图上1 cm代表实际500 m) 代 参考答案 1.B 2.D 3.C 4.解:小明家在学校北偏西50°的方向上,且距离学校500 m处. 学校在小明家南偏东50°的方向上,且距离小明家500 m处. 5.解:新华书店在学校北偏西40°的方向上,且距学校800 m处. 少年宫在学校南偏西20°的方向上,且距学校1 600 m处. 超市在学校北偏东60°的方向上,且距学1 100 m 处. 课堂小结 布置作业 教材第32页习题. 板书设计 第十九章 平面直角坐标系 19.1 确定平面上物体的位置 教学反思 教学反思 教学反思 教学反思 教学反思
第十九章 平面直角坐标系
19.2 平面直角坐标系
第1课时 平面直角坐标系
教学目标 1、理解平面直角坐标系以及横轴、纵轴、原点、坐标轴等概念. 2、能在给定的直角坐标系中,由点的位置写出它的坐标. 教学重难点 重点:理解平面直角坐标系以及横轴、纵轴、原点、坐标轴等概念. 难点:能在给定的直角坐标系中,由点的位置写出它的坐标. 教学过程 导入新课 回顾旧知: 我们已经学过了数轴,知道数轴上的点与实数一一对应,在建立了数轴之后,我们就可以确定直线上点的位置,如图. 学生思考: 点A代表的数字为( ﹣4 ) 点B代表的数字为( 2 ) -1所对应的点是( C ) 5所对应的点是( D ) 教师提问:那么,如何确定平面内点的位置呢? 引入新课:平面直角坐标系. 探究新知 如图是某城市部分街道的示意图.在繁星大道和中山路的交叉口点O处,小亮向交警叔叔问路. 提问:(1)按照交警的指示,小亮能找到图书大厦吗? (2)如果约定以点O处为参照点,先说出向东(或向西)方向上的距离,再说向北(或向南)方向上的距离,那么图书大厦附近交叉路口P点可以怎样表示? 学生思考后回答:(1)能;(2)P(东3 km,北2 km). 如果我们把中山路看成一条数轴(向东的方向为正),把繁星大道看成另一条数轴(向北的方向为正),把它们的交点O看成两条数轴的公共原点,以1 km作为数轴的单位长度,那么点P的位置就可以用一对数(3,2)来表示. 学生接着观察图片,并思考下列问题: (1)点A,B,C的位置应如何表示? (2)你能在图中找到用(3,-1.5),(-2,2)表示的点的位置吗? (3)街道所在平面上的任何一点,它的位置都可以用一对数表示出来吗?举例说明. 学生独立思考,动手操作. 探究1 平面直角坐标系 教师引导学生探究平面直角坐标系的定义. 学生动手操作: 指出点B的坐标,记作B(-4,1). 通过学习点A坐标的确认方法,并让学生说M,N,P,Q的坐标. 点M坐标为(3.5,2);点N坐标为(-4,3); 点P坐标为(-3,-2); 点Q坐标为(4,-2). 通过上面的练习,师生共同总结出确定点的位置的方法. 想一想: 知道了点的坐标,如何确定点的位置呢? 在平面直角坐标系中找到点A(3,-2). 教师指导学生完成例1的学习. 例1 如图,在平面直角坐标系中,描出点A(0,4),B(4,2),C(2,-3),D(-2,-3),E(-4,2),并依次连接ABCDEA. 解:在y轴上描出表示4的点,即得A(0,4).分别过x轴上表示4的点和y轴上表示2的点,作x轴和y轴的垂线,两条垂线的交点就是点B(4,2). 同理,可以描出C,D,E三点. 依次连接ABCDEA,得到图中所示的图形. 教师小结:实数与数轴上的点具有一一对应关系,由此可知,坐标平面上的点与有序实数对具有一一对应关系,即坐标平面上任意一点都可以用唯一一对有序实数来表示;反过来,任意一对有序实数都可以表示坐标平面上唯一一个点. 课堂练习 1.如图所示,这是某城市部分简图,每个小正方形的边长为1个单位长度,以火车站所在的位置为坐标原点建立平面直角坐标系,并分别写出各场所的坐标. 2.如图所示,这是某城市部分简图,每个小正方形的边长为1个单位长度,以火车站所在的位置为坐标原点建立平面直角坐标系,并分别写出各场所的坐标. 3.如图,点A的坐标为( ) A.(-2,3) B.(2,-3) C.(-2,-3) D.(2,3) 4.如图,点A的坐标为 ,点B的坐标为 . 5.在直角坐标系中描出下列各点: A(4,3),B(-2,3),C(-4,-1),D(2,-2). 参考答案 1.解:如图所示,建立平面直角坐标系,可得医院的坐标为(-2,-2),文化馆的坐标为(-3,1),体育场的坐标为(-4,3),宾馆的坐标为(2,2),市场的坐标为(4,3),超市的坐标为(2,-3). 2.解:如图所示,建立平面直角坐标系,可得医院的坐标为(-1,0),文化馆的坐标为(-2,3), 体育场的坐标为(-3,5),宾馆的坐标为(3,4),市场的坐标为(5,5), 超市的坐标为(3,-1). 3.A 4.(-2,0) (0,-2) 5. S 课堂小结 布置作业 教材第37页习题A组第1,3题. 板书设计 第十九章 平面直角坐标系 19.2 平面直角坐标系 平面直角坐标系 教学反思 教学反思 教学反思 教学反思 教学反思 教学反思
第十九章 平面直角坐标系
19.2 平面直角坐标系
第2课时 平面直角坐标系中点的坐标特征
教学目标 1.掌握平面直角坐标系中各象限、坐标轴上点的坐标特征. 2.掌握点关于坐标轴及原点的对称点的坐标特征. 教学重点难点 重点:掌握平面直角坐标系中各象限、坐标轴上点的坐标特征. 难点:掌握点关于坐标轴及原点的对称点的坐标特征. 教学过程 导入新课 回顾旧知: 我们知道了可以用有序实数对来表示平面上点的位置.而在实际应用中,我们往往要先建立平面直角坐标系. 在平面内,画两条有公共原点且互相垂直的数轴,就构成了平面直角坐标系,简称直角坐标系.水平方向的数轴叫做x轴(或横轴),取向右为正方向;竖直方向叫做y轴(或纵轴),取向上为正方向.x轴与y轴的公共原点叫做坐标原点. 两条数轴统称为坐标轴. 回忆上节课所学的知识,加深学生对定义的理解,从而引出本节课的内容. 探究新知 注意:1.数字必须是中文大写一、二、三、四. 2.坐标轴上的点不属于任何一个象限. 如图,平面直角坐标系的两条坐标轴将平面分成了四部分,从右上角的部分说起,按逆时针方向,各部分依次叫做第一象限、第二象限、第三象限和第四象限. 选出一名同学上黑板任画一平面直角坐标系,然后说明第一象限、第二象限、第三象限、第四象限的位置.明确坐标轴上的点不属于任何象限. 探究1 象限内、坐标轴上点的特征 如图所示,八边形ABCDEFGH与两条坐标轴的交点分别是M,N,P,Q四点. 学生分组讨论: (1)分别写出图中各点的坐标. (2)观察各点坐标,你认为同一象限内点的坐标的共同特点是什么? (3)指出坐标轴上点的坐标的共同特点. 学生观察图形,分析问题,互相交流. 学生回答后,小结: 1.A(3,1),B(1,3),C(-1,3),D(-3,1),E(-3,-1),F(-1,-3),G(1,-3) , H(3,-1),P(0,3),Q(0,-3), M(3,0),N(-3,0). 2.同一象限内点的横、纵坐标符号分别相同. 3.x轴上的点的纵坐标都是0,y轴上的点的横坐标都是0. 练一练:分别说出下列各点在哪个象限内或在哪条坐标轴上? A(6,-2),B(0,3),C(3,7),D(-6,-3),E(-2,0),F(-9,5). 思考:任一点P(x,y). (1)如果P(x,y)在第二象限,那么x,y分别是正数还是负数? (2)如果x>0,y<0,P(x,y)在第几象限? 引导学生思考上面的问题,总结出四个象限内点的坐标的特征,并画出下面帮助学生记忆. 分析总结:第一、二、三、四象限内点的坐标的符号分别是 (+,+), (-,+) , (-,-), (+,-). 探究2 关于x轴,y轴和原点对称的点的特征 如图所示,八边形ABCDEFGH与两条坐标轴的交点分别是M,N,P,Q四点. 点B关于x轴的对称点是G(1,-3); 点B关于y轴的对称点是C(-1,3); 点B关于原点的对称点是F(-1,-3). 观察图片,讨论:分别写出点B(1,3)关于x轴的对称点坐标,关于y轴的对称点坐标,关于原点的对称点坐标.关于x轴,y轴和原点的对称点的特征分别是什么? 共同归纳: (1)关于x轴对称的两点横坐标相同,纵坐标互为相反数; (2)关于y轴对称的两点横坐标互为相反数,纵坐标相同; (3)关于原点对称的两点横、纵坐标都互为相反数. 出示例2:建立直角坐标系,并解决下列问题. (1)描出下列各点,并把各点依次连接成封闭图形. A(1,-1),B(3,-1),C(3,1),D(1,1),E(1,3),F(-1,3),G(-1,1),H(-3,1), I(-3,-1),J(-1,-1),K(-1,-3),L(1,-3). (2)观察所得的图形,它是轴对称图形吗?如果是轴对称图形,画出它的对称轴. (3)在画出的图形中,分别写出关于x轴,y轴和原点的对称点. 解:(1)描点,连线后得到的图形如图所示. (2)这个图形是轴对称图形,它有四条对称轴:x轴,y轴,l1,l2. (3)关于x轴的对称点分别是点A和点D,点B和点C,点E和点L,点F和点K,点G和点J,点H和点I.关于y轴的对称点分别是点A和点J,点B和点I,点C和点H,点D和点G,点E和点F,点L和点K.关于原点的对称点分别是点A和点G,点B和点H,点C和点I,点D和点J,点E和点K,点F和点L. 说明:描点的过程中,教师要巡视指导,发现错误及时纠正. 师生共同总结:平面直角坐标系中相关点的坐标的特征 (1)在平面直角坐标系中,x轴和y轴将平面分成四个部分,按逆时针方向依次叫做第一象限、第二象限、第三象限、第四象限.坐标轴上的点不属于任何一个象限. (2)各象限内点的坐标有以下特征:如果点A(x,y)在第一象限,那么x>0,y>0;如果点A(x,y)在第二象限,那么x<0,y>0;如果点A(x,y)在第三象限,那么x<0,y<0;如果点A(x,y)在第四象限,那么x>0,y<0. (3)如果点A(x,y)在x轴上,那么y=0,x为任意实数;如果点A(x,y)在y轴上,那么x=0,y为任意实数;如果点A(x,y)既在x轴上又在y轴上,那么x=0且y=0. (4)平面直角坐标系中的点P(x,y),关于x轴对称点的坐标为(x,-y),关于y轴对称点的坐标为(-x,y),关于原点对称点的坐标为(-x,-y). 师生继续探讨: 相互交流,共同探讨: 点M(-3,4)到x轴、y轴和坐标原点的距离分别多少? MN=4,MH=3,MO=5. 小结: 总结规律 ①点P(a,b)到x轴的距离是|b|; ②点P(a,b)到y轴的距离是|a|; ③点P(a,b)到原点的距离是. 课堂练习 1.在平面直角坐标系中,点(1,5)所在的象限是 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.已知点P(0,a)在y轴的负半轴上,则点Q(-a2-1,-a+1)在 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 4.如图所示,点A(-2,1)到y轴的距离为( ) A.-2 B.1 C.2 D. 5.如图所示,下列各点在阴影区域内的是( ) A.(3,2) B.(-3,2) C.(3,-2) D.(-3,-2) 6.若点P(2k-1,1-k)在第四象限,则k的取值范围为( ) A.k>1 B.k< C.k> D.
19.3 坐标与图形的位置
教学目标 1.能建立适当的直角坐标系,描述图形的位置. 2.通过用直角坐标系表示图形的位置,使学生体会平面直角坐标系在实际问题中的应用. 教学重点难点 重点:能建立适当的直角坐标系,描述图形的位置. 难点:通过用直角坐标系表示图形的位置,使学生体会平面直角坐标系在实际问题中的应用. 教学过程 导入新课 复旧引新: 利用平面直角坐标系的知识,用坐标表示各个景点的位置: 想一想:同一个点在不同的坐标系中,坐标相同吗? 教师引导学生得出:同一个点在不同的坐标系中,坐标不相同. 2.利用平面直角坐标系的知识,说出下面各点的坐标. 通过复习有利于本节内容的学习,为下面内容的继续做好铺垫. 探究新知 小亮想把下面的四边形的形状通过电话告诉小强,让小强也能准确地画出相同的图形.他们该怎么做呢? 有人说:“建立个平面直角坐标系,告诉这个四边形四个顶点的坐标就能画出相同的图形”. 你认为这种说法可行吗?大家动手画一画吧. 在实际生活中,经常需要建立适当的直角坐标系,通过坐标来描述某个图形的位置与形状. 揭示课题:坐标与图形的位置. 大家思考一下: 直角坐标系建立的不同,点的坐标会怎么样呢? 活动1 已知一个边长是4的正方形.建立适当的直角坐标系,通过各顶点的坐标来描述它的位置. 学生小组内交流,得出: 解:如图,以顶点B为原点,BC所在直线为x轴,AB所在直线为y轴建立平面直角坐标系. 正方形四个顶点A,B,C,D的坐标分别为 A(0,4), B(0,0),C(4,0), D(4,4). 活动2 解:以正方形对角线的交点为原点,水平方向直线为x轴,竖直方向直线为y轴建立平面直角坐标系. 正方形四个顶点A,B,C,D的坐标分别为 A(-2,2),B(-2,-2),C(2, -2),D(2,2). 活动3 解:以正方形对角线的交点为原点,BD所在直线为x轴,AC所在直线为y轴建立平面直角坐标系. 正方形四个顶点A,B,C,D的坐标分别为 小组内先独立思考后,发表自己不同的看法,画图操作,并表示出顶点的坐标. 直角坐标系点A坐标点B坐标点C坐标点D坐标活动1(0,4)(0,0)(4,0)(4,4)活动2(-2,2)(-2,-2)(2,-2)(2,2)活动3
想一想:这三种建立直角坐标系的方式各有什么优点?说明你的理由. 学生得出:这样建立直角坐标系会很方便的表示出点的坐标,便于观察和计算. 小结:建立不同的直角坐标系,同一个图形的顶点坐标也不同,应根据具体情况建立适当的直角坐标系. 注意: (1)建立直角坐标系的方法有很多,由于坐标系的选择直接影响计算的繁简程度,所以建立直角坐标系时,要以能简捷地确定平面内点的坐标为原则. (2)建立新的直角坐标系确定几何图形上点的坐标,应充分考虑到易于求点到坐标轴的距离.否则,计算麻烦,有时根本无法确定这些点的坐标. 练一练: 如图所示,在等腰三角形ABC中,底边BC=4,高AD=6. (1)请你建立适当的直角坐标系,并写出点A,B,C的坐标. (2)说明你选择这个直角坐标系的理由. 学生思考后得出:(1)以线段BC所在直线为x轴,线段DA所在直线为y轴,建立直角坐标系,则A(0,6),B(-2,0),C(2,0). (2)理由:这样建立的平面直角坐标系,能保证等腰三角形的顶点都在坐标轴上,便于书写出顶点的坐标. 教师指明:体现了轴对称性. 另一名同学思考后,得出:以B为坐标原点,BC所在直线为x轴,过点B且垂直于BC的直线为y轴建立平面直角坐标系. A(2,6),B (0,0), C (4,0). 学生们各抒已见,发表自己的看法. 议一议:建立坐标系常用的方法有哪些? 小结: 课堂练习 1.一个长方形在平面直角坐标系中,它的三个顶点的坐标分别为(-3,-1),(2,-1),(2,2),则第四个顶点的坐标为( ) A.(-3,2) B.(3,2) C.(-3,-4) D.(7,2) 2.如图所示,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为( ) A.(3,1) B.(-1,1) C.(3,5) D.(-1,5) 3.如图所示,将长为3 cm的长方形ABCD放在平面直角坐标系中,若点D(6,3),则A点的坐标为( ) A.(5,3) B.(4,3) C.(4,2) D.(3,3) 4.如图所示,正方形ABCD中点A和点C的坐标分别为(-2,3)和(3,-2),则点B和点D的坐标分别为( ) A.(2,2)和(3,3) B.(-2,-2)和(3,3) C.(-2,-2)和(-3,-3) D.(2,2)和(-3,-3) 5.如图所示,长方形ABCD中,AB=3,BC=4,且点A在坐标原点,则C点的坐标为( ) A.C(4,3) B.C(4,-3) C.C(3,-4) D.C(-4,-3) 6.一个直角三角形ABC的两条直角边为3和4,现在把它放在不同的坐标系中,请写出各顶点的坐标. 参考答案 1.A 2.C 3.D 4.B 5.B 6. 课堂小结 布置作业 教材第43页习题A组第1,2 题. 板书设计 第十九章 平面直角坐标系 19.3 坐标与图形的位置 教学反思 教学反思 教学反思 教学反思 教学反思 教学反思
第十九章 平面直角坐标系
19.4 坐标与图形的变化
第1课时 图形的平移与坐标变化
教学目标 1、掌握点平移得到新坐标的规律,并且熟练画出图形. 2、理解“数形结合”,体会坐标系中图形平移的实际应用. 教学重难点 重点:掌握点平移得到新坐标的规律,并且熟练画出图形. 难点:理解“数形结合”,体会坐标系中图形平移的实际应用. 教学过程 导入新课 教师提问: 1、你还记得什么叫平移吗? 在平面内,把一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移. 2、图形平移的性质是什么? (1)新图形与原图形形状和大小不变,但位置改变; (2)对应点的连线平行且相等. 课前小练 如图所示,长方形公园ABCD的长、宽分别是6千米、4千米,以公园中心O为原点建立直角坐标系,写出各顶点的坐标. A(3,2),B(-3,2),C(-3,-2),D(3,-2). 【学生思考】 (1)观察上图,由点B到点A是怎样移动的?(点B向右移动6个单位长度得到点A) (2)在图中,你还能看到由一点怎样移动得到另一点? 探究新知 1、探究坐标系中点的平移 活动1 根据上图回答问题: 将点A(-2,-3)向右平移5个单位长度,得到点A1( 3 , -3); (2)将点A(-2,-3)向左平移2个单位长度,得到点A2(-4 , -3); (3)将点A(-2,-3)向上平移4个单位长度,得到点A3(-2 , 1 ) ; (4)将点A(-2,-3)向下平移2个单位长度,得到点A4(-2 , -5 ). 师生互动: 教师引导学生观察并思考,点A左右平移时哪个坐标发生变化,是如何变化的? 当点A上下平移时那个坐标发生变化,是如何变化的? 活动2 在坐标平面上,一只蚂蚁从原点出发,爬行的路径如图所示. 写出A,B,C,D,E这五个点的坐标. A(0,2),B(3,2),C(3,-2),D(-3,-2),E(-3,3). (2)指出蚂蚁在各条线段上爬行的方向和距离,并填写下表. 移动的路径平移的方向和距离坐标的变化横坐标纵坐标O(0,0)→A(0,2)向上平移2个单位长度不变加2A(0,2)→B(3,2)向右平移3个单位长度加3不变B(3,2)→C(3,-2)向下平移4个单位长度不变减4C(3,-2)→D(-3,-2)向左平移6个单位长度减6不变D(-3,-2)→E(-3,3)向上平移5个单位长度不变加5
(3)观察各点的坐标变化,当P(x,y)沿x轴左右平移时坐标有什么变化?当点P(x,y)沿y轴上下平移时坐标有什么变化? 师生总结: 点沿x轴平移时,纵坐标不变,横坐标左减右加;点沿y轴平移时,横坐标不变,纵坐标上加下减. 探究坐标中图形的平移 例:如图所示,在平面直角坐标系中,长方形ABCD各顶点的坐标分别为A(-2,1),B(2,1),C(2,3),D(-2,3).将长方形ABCD沿x轴的方向向右平移5个单位长度,得到长方形A1B1C1D1.请写出长方形A1B1C1D1各顶点的坐标,并指出对应顶点坐标的变化规律. 学生活动 自主完成.将长方形ABCD沿x轴的方向向右平移5个单位长度,各顶点移动的方向一致,移动的距离都是5个单位长度.因此,平移后的长方形A1B1C1D1各顶点的坐标为A1(3,1),B1(7,1),C1(7,3),D1(3,3). 观察与思考: 图形的平移可以转化为哪几个点的平移? (2)这几个点的平移是否一致? (3)在平移中,各点的坐标分别发生了怎样的变化? 师生总结: 顶点坐标的变化规律为:长方形A1B1C1D1各顶点的横坐标是将长方形ABCD各顶点的横坐标都增加5,纵坐标不变而得到的. 3、深化理解,总结规律 在例题的图中,将长方形ABCD沿y轴的方向向下平移4个单位长度,画出平移后的长方形,写出各顶点的坐标,并说出图形平移前后对应顶点的坐标是如何变化的. A(-2,1)→A1(-2,-3), B(2,1)→B1(2,-3), C(2,3)→C1(2,-1), D(-2,3)→D1(-2,-1). 总结规律:平移后的长方形各顶点纵坐标是由长方形ABCD各顶点的纵坐标都减少4,横坐标不变得到的. 2.若将长方形ABCD先沿x轴的方向向右平移6个单位长度,再沿y轴的方向向下平移5个单位长度,画出平移后的长方形,写出其各顶点的坐标,并说出图形平移前后对应顶点的坐标是如何变化的. A(-2,1)→A2(4,-4), B(2,1)→B2(8,-4), C(2,3)→C2(8,-2), D(-2,3)→D2(4,-2). 总结规律:平移后的长方形各顶点横坐标是由长方形ABCD各顶点横坐标增加6,纵坐标是由其纵坐标减少5得到的. 教师提问: 一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系? 师生总结: (1)直角坐标系中,沿横轴平移,图形上每一点的纵坐标不变,而横坐标增减,简记“左减右加”;沿纵轴平移,横坐标不变,纵坐标增减,简记“上加下减”.“左减右加,上加下减”也可这样理解:沿x轴(y轴)正方向平移,则横(纵)坐标加上平移的单位数量,沿x轴(y轴)负方向平移,则横(纵)坐标减去平移的单位数量即可. (2) ①原图形向左(右)平移k个单位长度(k>0): 原图形上的点P(x,y)P1(x+k,y); 原图形上的点P(x,y)P2(x-k,y); ②原图形向上(下)平移k个单位长度(k>0): 原图形上的点P(x,y)P3(x,y+k); 原图形上的点P(x,y)P4(x,y-k). (3)在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数k,得到的新图形就是把原图形向右(或向左)平移k个单位长度;如果把一个图形各个点的纵坐标都加(或减去)一个正数k,得到的新图形就是把原图形向上(或向下)平移k个单位长度. 课堂练习 1.如图所示,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为 ( ) A.(2,-1) B.(2,3) C.(0,1) D.(4,1) 2.如图所示,把线段AB平移,使得点A到达点C(4,2),点B到达点D,那么点D的坐标是 ( ) A.(7,3) B.(6,4) C.(7,4) D.(8,4) 3.将点M(-1,-5)向右平移3个单位长度得到点N,则点N所在的象限是 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 4.如图所示,A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为 ( ) A.2 B.3 C.4 D.5 5.在平面直角坐标系中,将三角形各点的横坐标都减去3,纵坐标保持不变,所得图形与原图形相比 ( ) A.向右平移了3个单位 B.向左平移了3个单位 C.向上平移了3个单位 D.向下平移了3个单位 参考答案 1.A 2.C 3.D 4.A 5.B 课堂小结 布置作业 教材第46页习题A组第2,3题. 板书设计 第十九章 平面直角坐标系 19.4 坐标与图形的变化 第1课时 图形的平移与坐标变化 教学反思 教学反思 教学反思 教学反思 教学反思 教学反思
第十九章 平面直角坐标系
19.4 坐标与图形的变化
第2课时 图形的轴对称、放缩与坐标变化
教学目标 1、在同一直角坐标系内,感受坐标变化而使图形对称、扩大和缩小的过程,并能得出图形对称、扩大和缩小的规律. 2、通过探索图形上点的坐标变化与图形变换之间的关系,进一步体会数形结合的数学思想. 教学重难点 重难点:在同一直角坐标系内,感受坐标变化而使图形对称、扩大和缩小的过程,并能得出图形对称、扩大和缩小的规律. 教学过程 导入新课 出示问题,回忆旧知 什么叫轴对称图形? 沿着某一直线对折,直线两旁的部分能够完全重合的图形就是轴对称图形,这条直线称为对称轴. 学生活动: 1、动手画一画:已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗? 2、画出这些点分别关于x轴、y轴对称的点,并填写表格. 已知点A(2,-3)B(-1,2)C(-6,-5)D(3,5)E(4,0)F(0,-3)关于x轴的对称点(2,3)(-1,-2)(-6,5)(3,-5)(4,0)(0,3)关于y轴的对称轴(-2,-3)(1,2)(6,-5)(-3,5)(-4,0)(0,-3)
观察并思考:关于坐标轴对称的两个点的坐标有什么变化规律? 这样引导学生回忆轴对称图形的相关知识,并进行点的对称方面的作图与练习,为本节课知识的学习的打下了良好基础. 探究新知 1.探究成轴对称的两个图形的坐标变化 如图所示,在平面直角坐标系中,△ABC各顶点的坐标分别为: A(-5,1),B(-1,1),C(-2,4). 学生活动: (1)分别把点A,B,C关于x轴和y轴的对称点的坐标填写在下表中. (2)将A1,B1,C1连接起来,观察△A1B1C1与△ABC有什么位置关系? (3)将A2,B2,C2连接起来,观察△A2B2C2与△ABC有什么位置关系? (4)总结关于x轴成轴对称的两个图形的对应点的坐标之间有什么关系?关于y轴成轴对称时呢? △ABC顶点坐标A(-5,1)B(-1,1)C(-2,4)关于x轴的对称点A1(-5,-1)B1(-1,-1)C1(-2,-4)关于y轴的对称点A2(5,1)B2(1,1)C2(2,4)
总结: 关于x轴成轴对称的两个图形,各对应顶点的横坐标相等,纵坐标互为相反数; 关于y轴成轴对称的两个图形,各对应顶点的横坐标互为相反数,纵坐标相等. 学生活动:练一练 如图,左右两幅图案关于y轴对称,右侧图案中的左右眼睛的坐标分别是(2,3),(4,3).嘴角左右端点的坐标分别是(2,1),(4,1). 试确定左侧图案中的左右眼睛和嘴角左右端点的坐标. 答:左侧图案中的左眼坐标为(-4,3),右眼坐标为(-2,3),嘴角的左端点坐标为(-4,1),右端点坐标为(-2,1). 探究图形放缩的坐标变化 活动1: 如图所示,在直角坐标系中,五边形OABCD各顶点的坐标分别为: O(0,0),A(0,2),B(2,3),C(4,2),D(3,0). (1)将各顶点的横坐标和纵坐标都乘2,写出各对应点的坐标. O(0,0), A1(0,4), B1 (4,6),C1(8,4), D1(6,0). (2)在直角坐标系中,描出各点,然后依次连接,画出五边形OA1B1C1D1. O(0,0), A1 (0,4), B1 (4,6), C1 (8,4), D1 (6,0). (3)思考:两个五边形的形状、大小有什么变化? 形状没有发生变化,各边的长度变为原来的2倍,并且对应顶点的连线所在的直线都相交于一点. 活动2: 如图所示,说出O,A,B,C各点的坐标. O(0, 0),A (2, 6) ,B(6, 6) ,C(8,0). (2)把各顶点的横坐标和纵坐标都乘,分别写出各顶点坐标.然后画出图形,观察得到的图形与原图形的形状和大小的变化规律. O(0, 0) ,A1(1,3) ,B1(3,3) ,C1(4, 0). 形状没有发生变化,各边的长度变为原来的,且对应顶点的连线所在的直线都相交于一点. (3)观察并思考:将一个图形各顶点的横坐标和纵坐标都乘k,图形的形状和大小有什么变化? 师生总结: 将一个图形各顶点的横坐标和纵坐标都将一个图形各顶点的横坐标和纵坐标都乘k,所得图形的形状不变,各边扩大到原来的k倍且连接各对应顶点的直线相交于一点. 课堂练习 1.平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( ) A.y轴对称 B.x轴对称 C.原点对称 D.直线y=x对称 2.在平面直角坐标系中,将点A(-1,2)向右平移3个单位长度得到点B,则点B关于x轴的对称点C的坐标是( ) A.(-4,-2) B.(2,2) C.(-2,2) D.(2,-2) 3.如图所示,△ABC的顶点都在正方形网格格点上,点A的坐标为(-1,4).将△ABC沿y轴翻折到第一象限得到△A′B′C′,则点C的对应点C′的坐标是( ) A.(3,1) B.(-3,-1) C.(1,-3) D.(3,-1) 4.在平面直角坐标系中,等边三角形OAB关于x轴对称的图形是等边三角形OA′B′.若已知点A的坐标为(6,0),则点B′的横坐标是 ( ) A.6 B.-6 C.3 D.-3 5.在平面直角坐标系中,△ABC的位置如图所示,点A的坐标为(1,3),将△ABC先向左平移3个单位,再作出其关于x轴的对称图形,则A点的对应点的坐标为 ( ) A.(-3,-2) B.(-1,-2) C.(-2,-2) D.(-2,-3) 6.如图所示,△ABO缩小后变为△A′B′O,其中A,B的对应点分别为A′,B′,点A,B,A′,B′均在图中格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( ) A. B.( m,n) C. D. 7.在平面直角坐标系中,规定把一个正方形先沿着x轴翻折,再向右平移2个单位长度称为1次变换.如图,已知正方形ABCD的顶点A,B的坐标分别是(-1,-1)、(-3,-1),把正方形ABCD经过连续7次这样的变换得到正方形A′B′C′D′,求B的对应点B′的坐标. 参考答案 1.B 2.D 3.A 4.C 5.D 6.D 7.解:∵ 正方形ABCD,点A,B的坐标分别是(-1,-1)、(-3,-1), 根据题意,得第1次变换后的点B的对应点的坐标为(-3+2,1),即(-1,1), 第2次变换后的点B的对应点的坐标为(-1+2,-1),即(1,-1), 第3次变换后的点B的对应点的坐标为(1+2,1),即(3,1),…, 第n次变换后的点B的对应点的为:当n为奇数时为(2n-3,1),当n为偶数时为(2n-3,-1), ∴ 把正方形ABCD经过连续7次这样的变换得到正方形A′B′C′D′,则点B的对应点B′的坐标是(11,1). 课堂小结 布置作业 教材第61页习题A组第1,2题. 板书设计 第十九章 平面直角坐标系 19.4 坐标与图形的变化 第2课时 图形的轴对称、放缩与坐标变化 教学反思 教学反思 。 教学反思 教学反思 教学反思 教学反思 教学反思
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
