2.2 探索直线平行的条件(第1课时)教学课件 北师大版中学数学七年级(下)
文档属性
| 名称 | 2.2 探索直线平行的条件(第1课时)教学课件 北师大版中学数学七年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:07:33 | ||
图片预览




文档简介
(共22张PPT)
第 二 章 相交线与平行线
2.2 探索直线平行的条件
第1课时 利用同位角判定两条直线平行
学习目标
1.理解并掌握同位角的概念,能够判定同位角;
2.能够运用同位角相等判定两直线平行;(重点、 难 点)
3.理解并掌握平行公理及其推论,能够运用其解决
实际问题.(难点)
新课引入
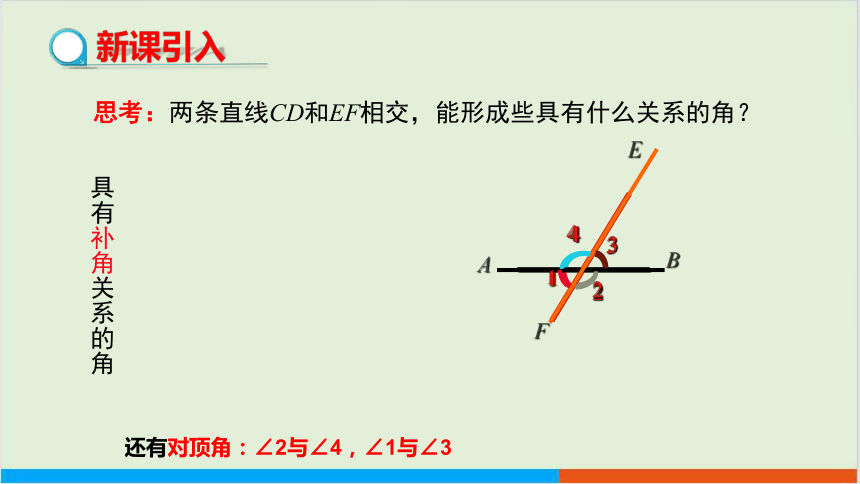
思考:两条直线CD和EF相交,能形成些具有什么关系的角?
3
2
2
1
3
4
1
4
A
B
E
F
1
3
4
2
具有补角关系的角
还有对顶角:∠2与∠4,∠1与∠3
6
7
5
8
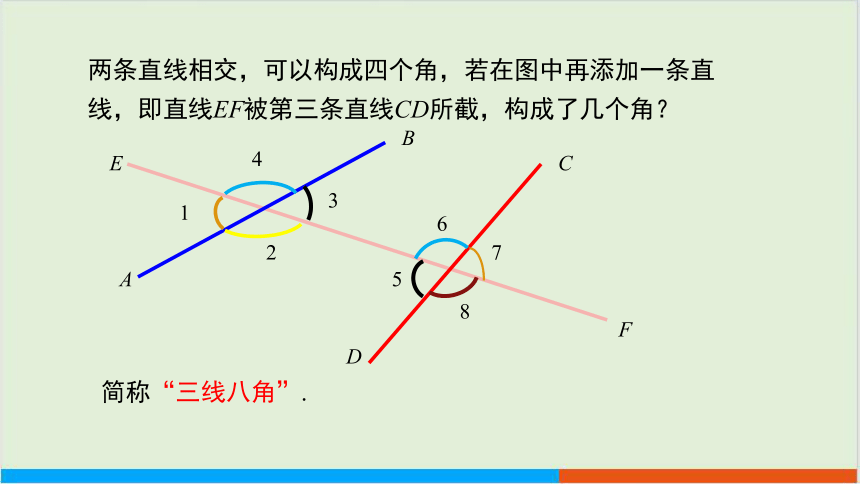
简称“三线八角”.
两条直线相交,可以构成四个角,若在图中再添加一条直线,即直线EF被第三条直线CD所截,构成了几个角?
B
A
F
E
C
D
4
3
1
2
情景导入
如图,装修工人正在向墙上钉木条.如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角是多少度时,才能使木条a与木条b平行?
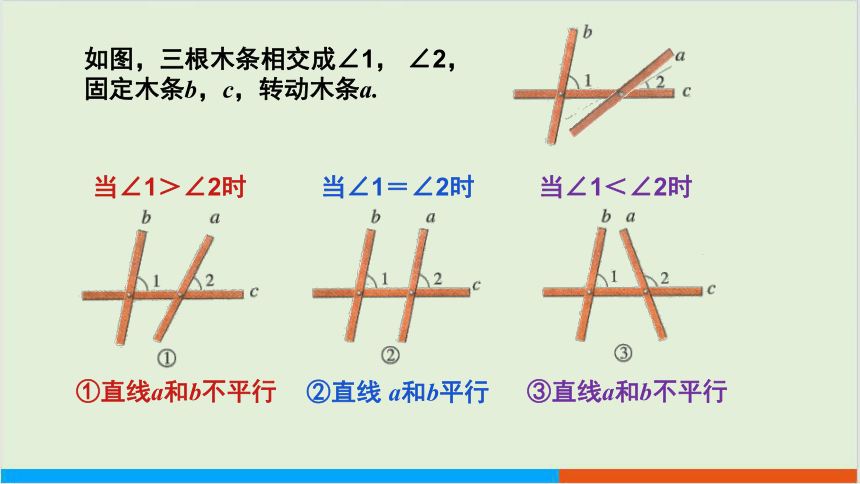
如图,三根木条相交成∠1, ∠2,固定木条b,c,转动木条a.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线 a和b平行
③直线a和b不平行
知识讲解
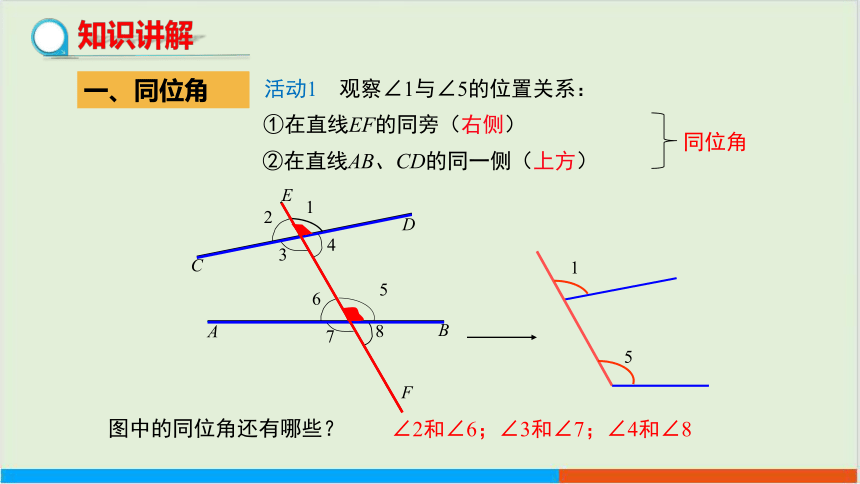
一、同位角
F
活动1 观察∠1与∠5的位置关系:
①在直线EF的同旁(右侧)
②在直线AB、CD的同一侧(上方)
C
A
D
B
E
1
2
3
4
5
6
7
8
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
1
5
C
A.(1)(2) (3) B.(3)(4)
C.(1)(2) D.(2)(3) (4)
练一练:下列图形中,∠1和∠2是同位角的有( )
1
2
1
2
1
2
1
2
(1) (2) (3) (4)
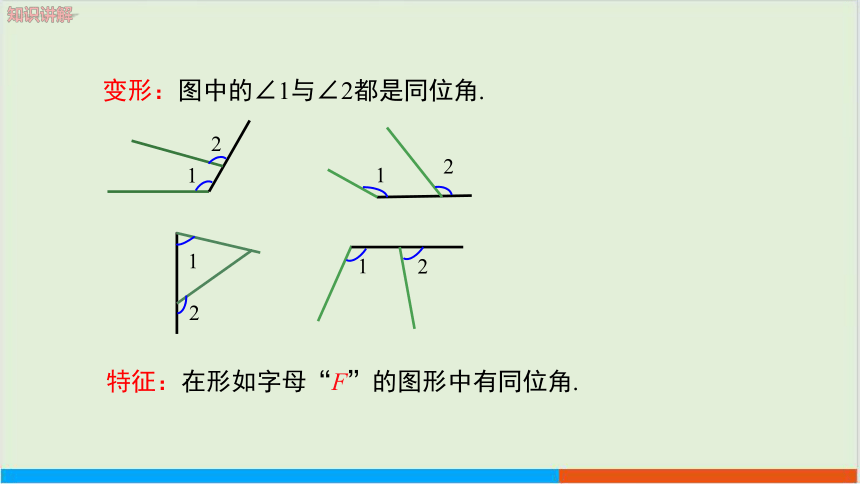
特征:在形如字母“F”的图形中有同位角.
变形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
二、利用同位角判定两条直线平行
用三角尺和直尺画平行线的方法:
(1)放
(2)靠
(3)推
(4)画
b
A
2
1
a
B
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
思考:
判定方法:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
应用格式:
因为∠1=∠2(已知),
所以l1∥l2
(同位角相等,两直线平行).
1
2
l2
l1
A
B
我们通常用“//” 表示平行.
C
B
A
D
a ∥ b
AB ∥ CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
平行线的表示法
练一练:
如图, ∠1=55 , ∠2=125 ,直线AB与CD平行吗?为什么
A
C
E
F
B
D
1
2
M
N
平行.
同位角相等,两直线平行.
你能说出木工师傅用图中的角尺工具画平行线的道理吗?
同位角相等,两直线平行.
三、平行于同一条直线的两条直线平行
·
A
·
B
(3)经过点C能画出几条直线与直线AB平行?
(4)过点D画一条直线与直线AB平行,与(3)中所画的直线平行吗?
·
·
C
D
(1)经过点C能画出几条直线?
无数条
1条
a
b
(2)与直线AB平行的直线有几条?
无数条
结论:经过直线外一点有且只有一条直线与已知直线平行.
平行
几何语言表达:
c
b
a
平行线的性质(平行线的传递性):
平行于同一条直线的两条直线平行.
因为a//c , c//b(已知)
所以a//b(平行于同一条直线的两条直线平行).
随堂训练
1.下列图形中,∠1与∠2是同位角的是( )
B.
C.
D.
A.
A
2.同一平面内,直线与两条平行线的位置关系是( )
A.与平行或相交
B.可能与平行,与相交
C.与一定都相交
D.可能与垂直,与平行
A
3.下列推理正确的是( )
A.因为a // d,b // c,所以c // d
B.因为a // c,b // d,所以c // d
C.因为a // b,a // c,所以b // c
D.因为a // b,c // d,所以a // c
C
4.从∠5=∠ ,可以推出AB∥CD,
理由是 .
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
课堂小结
特征 基本图形 代表字母
F
截线:同侧,
被截线:同旁
1
2
1.同位角
2.平行线
(1)同位角相等,两直线平行.
(3)平行于同一条直线的两条直线平行.
(2)经过直线外一点有且只有一条直线与这条直线平行.
第 二 章 相交线与平行线
2.2 探索直线平行的条件
第1课时 利用同位角判定两条直线平行
学习目标
1.理解并掌握同位角的概念,能够判定同位角;
2.能够运用同位角相等判定两直线平行;(重点、 难 点)
3.理解并掌握平行公理及其推论,能够运用其解决
实际问题.(难点)
新课引入
思考:两条直线CD和EF相交,能形成些具有什么关系的角?
3
2
2
1
3
4
1
4
A
B
E
F
1
3
4
2
具有补角关系的角
还有对顶角:∠2与∠4,∠1与∠3
6
7
5
8
简称“三线八角”.
两条直线相交,可以构成四个角,若在图中再添加一条直线,即直线EF被第三条直线CD所截,构成了几个角?
B
A
F
E
C
D
4
3
1
2
情景导入
如图,装修工人正在向墙上钉木条.如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角是多少度时,才能使木条a与木条b平行?
如图,三根木条相交成∠1, ∠2,固定木条b,c,转动木条a.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行
②直线 a和b平行
③直线a和b不平行
知识讲解
一、同位角
F
活动1 观察∠1与∠5的位置关系:
①在直线EF的同旁(右侧)
②在直线AB、CD的同一侧(上方)
C
A
D
B
E
1
2
3
4
5
6
7
8
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
1
5
C
A.(1)(2) (3) B.(3)(4)
C.(1)(2) D.(2)(3) (4)
练一练:下列图形中,∠1和∠2是同位角的有( )
1
2
1
2
1
2
1
2
(1) (2) (3) (4)
特征:在形如字母“F”的图形中有同位角.
变形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
二、利用同位角判定两条直线平行
用三角尺和直尺画平行线的方法:
(1)放
(2)靠
(3)推
(4)画
b
A
2
1
a
B
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
思考:
判定方法:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
应用格式:
因为∠1=∠2(已知),
所以l1∥l2
(同位角相等,两直线平行).
1
2
l2
l1
A
B
我们通常用“//” 表示平行.
C
B
A
D
a ∥ b
AB ∥ CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
平行线的表示法
练一练:
如图, ∠1=55 , ∠2=125 ,直线AB与CD平行吗?为什么
A
C
E
F
B
D
1
2
M
N
平行.
同位角相等,两直线平行.
你能说出木工师傅用图中的角尺工具画平行线的道理吗?
同位角相等,两直线平行.
三、平行于同一条直线的两条直线平行
·
A
·
B
(3)经过点C能画出几条直线与直线AB平行?
(4)过点D画一条直线与直线AB平行,与(3)中所画的直线平行吗?
·
·
C
D
(1)经过点C能画出几条直线?
无数条
1条
a
b
(2)与直线AB平行的直线有几条?
无数条
结论:经过直线外一点有且只有一条直线与已知直线平行.
平行
几何语言表达:
c
b
a
平行线的性质(平行线的传递性):
平行于同一条直线的两条直线平行.
因为a//c , c//b(已知)
所以a//b(平行于同一条直线的两条直线平行).
随堂训练
1.下列图形中,∠1与∠2是同位角的是( )
B.
C.
D.
A.
A
2.同一平面内,直线与两条平行线的位置关系是( )
A.与平行或相交
B.可能与平行,与相交
C.与一定都相交
D.可能与垂直,与平行
A
3.下列推理正确的是( )
A.因为a // d,b // c,所以c // d
B.因为a // c,b // d,所以c // d
C.因为a // b,a // c,所以b // c
D.因为a // b,c // d,所以a // c
C
4.从∠5=∠ ,可以推出AB∥CD,
理由是 .
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
课堂小结
特征 基本图形 代表字母
F
截线:同侧,
被截线:同旁
1
2
1.同位角
2.平行线
(1)同位角相等,两直线平行.
(3)平行于同一条直线的两条直线平行.
(2)经过直线外一点有且只有一条直线与这条直线平行.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
