2.2 探索直线平行的条件(第2课时)教学课件 北师大版中学数学七年级(下)
文档属性
| 名称 | 2.2 探索直线平行的条件(第2课时)教学课件 北师大版中学数学七年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:07:33 | ||
图片预览



文档简介
(共24张PPT)
第 二 章 相交线与平行线
2.2 探索直线平行的条件
第2课时 利用内错角、同旁内角
判定两条直线平行
学习目标
1.理解内错角、同旁内角的概念,结合图形识别内错角、同旁
内角;
2.会运用内错角、同旁内角判定两条直线平行.(重点、 难
点)
复习引入
我们已经学过的关于平行线内容有哪些?
平行于同一条直线的两条直线平行
经过直线外一点,有且只有一条直线与已知直线平行.
同位角相等,两直线平行.
思考:还有其他判定两条直线平行的方法吗?
知识讲解
一、内错角、同旁内角的概念
A
C
B
D
E
F
1
2
3
4
5
6
7
8
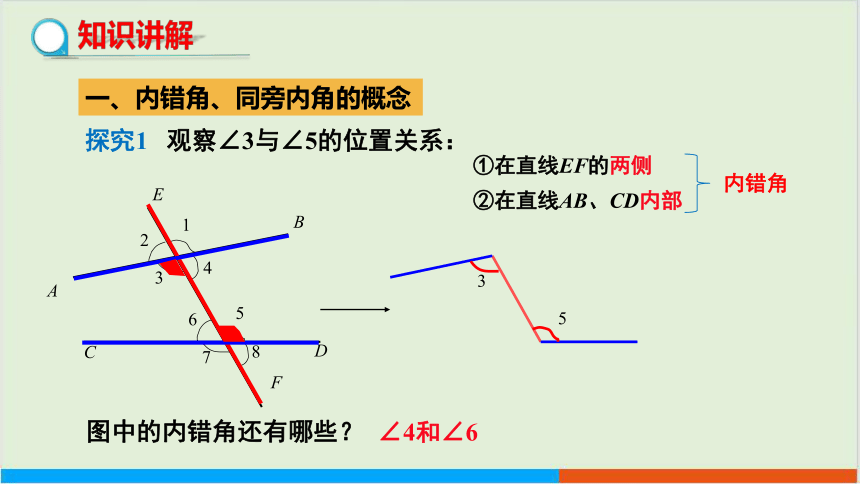
探究1 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB、CD内部
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
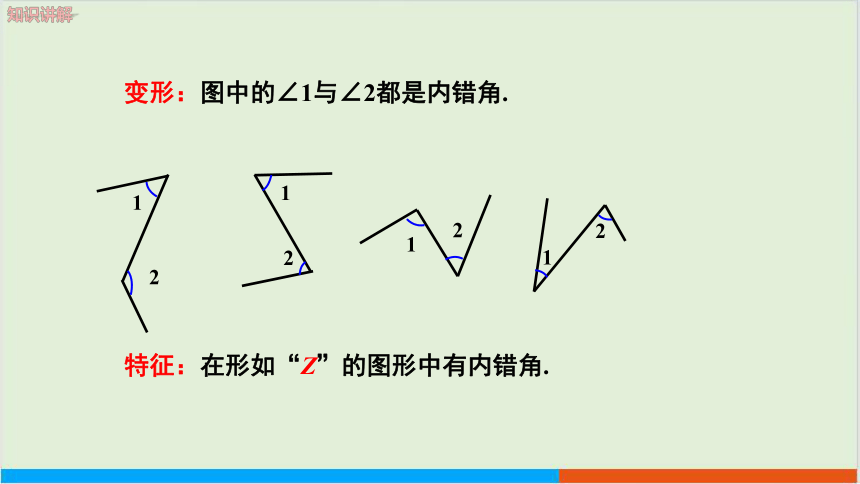
变形:图中的∠1与∠2都是内错角.
特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
A
C
B
D
E
F
1
2
3
4
5
6
7
8
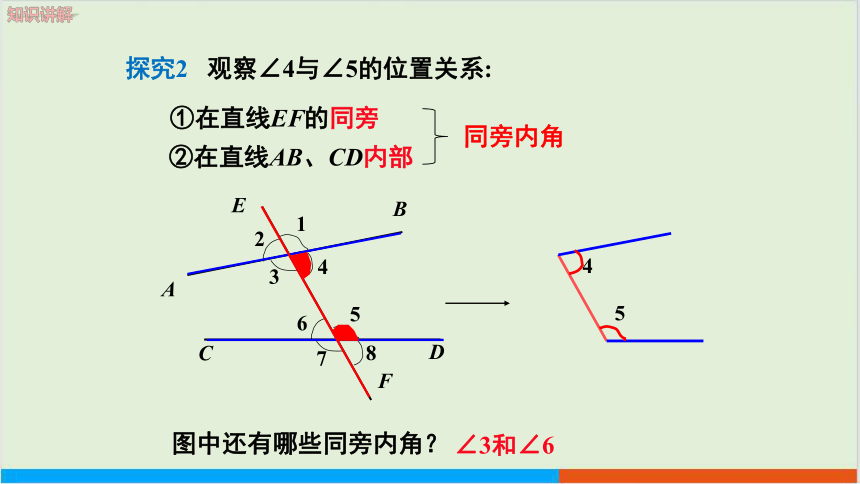
探究2 观察∠4与∠5的位置关系:
①在直线EF的同旁
②在直线AB、CD内部
4
5
∠3和∠6
图中还有哪些同旁内角?
同旁内角
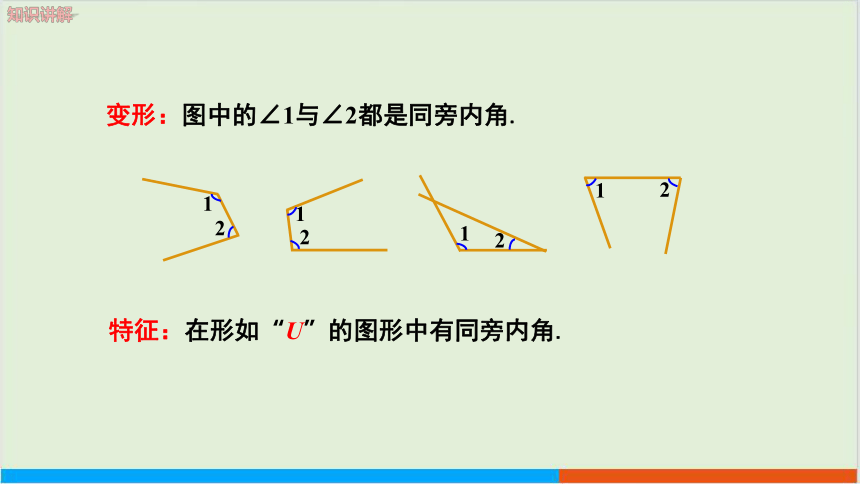
变形:图中的∠1与∠2都是同旁内角.
特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
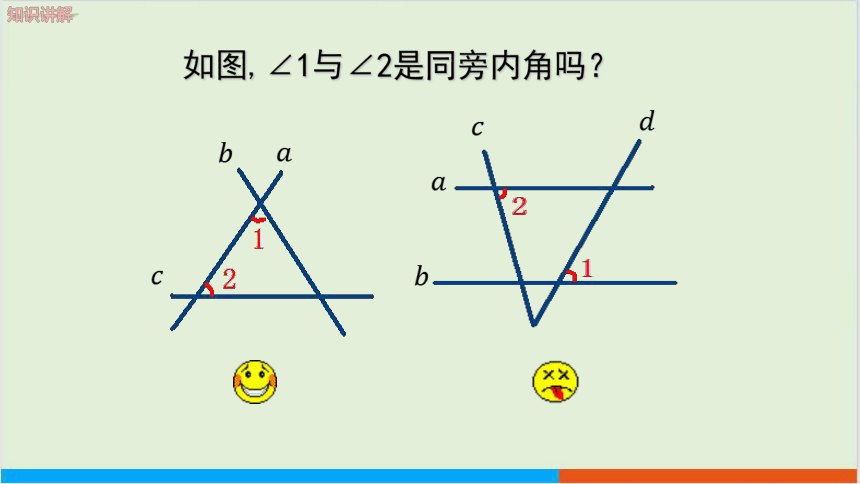
如图,∠1与∠2是同旁内角吗?
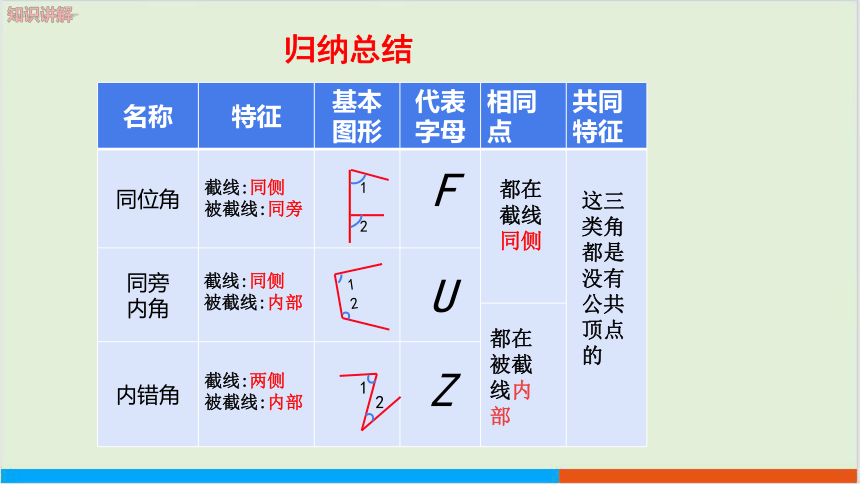
名称 特征 基本图形 代表字母 相同点 共同特征
同位角
同旁 内角 内错角 F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:内部
截线:两侧
被截线:内部
1
2
1
2
1
2
都在截线同侧
都在被截线内部
这三类角都是没有公共顶点的
归纳总结
例1 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,
E
D
C
B
A
8
7
6
5
4
3
2
1
同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.
二、利用内错角、同旁内角判定两条直线平行
问题1:如图,由 3= 2,可推出a//b吗?如何推出的呢?
2
b
a
1
3
a//b(同位角相等,两直线平行).
解:
∵ 1= 3(已知),
3= 2(对顶角相等),
1= 2,
判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠3=∠2(已知),
∴a∥b(内错角相等,两直线平行).
应用格式:
2
b
a
1
3
问题2 : 如图,如果 1+ 2=180° ,你能判定a//b吗
c
2
b
a
1
3
解:能,
∵ 1+ 2=180°(已知),
1+ 3=180°(邻补角的性质),
2= 3(同角的补角相等),
a//b(同位角相等,两直线平行).
判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
3
∵∠1+∠2=180°(已知),
∴a∥b(同旁内角互补,两直线平行).
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
① ∵ ∠1 =_____(已知),
∴ AB∥CE( ).
② ∵ ∠1 +_____=180o(已知),
∴ CD∥BF( ).
③ ∵ ∠1 +∠5 =180o(已知),
∴ _____∥_____( ).
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知),
∴ CE∥AB( ).
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
例 根据条件完成填空.
当图中各角满足下列条件时,你能指出哪两条直线平行
(1) ∠1 = ∠4;
(2) ∠2 = ∠4;
(3) ∠1 + ∠3 =180 ;
a
b
l
m
n
1
2
3
4
.
.
练一练
2.如图,下列说法中不正确的是( )
A.∠1和∠3是同旁内角
B.∠2和∠3是内错角
C.∠2和∠4是同位角
D.∠3和∠5是对顶角
随堂训练
1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B B. ∠1=∠A
C. ∠3=∠B D. ∠3=∠A
C
1
2
3
A
E
B
C
D
C
3.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠4=180°,则a∥c
C
4.如图,已知∠1=30°,∠2或∠3满足条件
,则a//b.
2
1
3
a
b
c
∠2=150°或∠3=30°
5、一弯形轨道的拐角°,那么当另一拐角 时,.
D
C
B
A
60
6.如图,给出下列条件:①;②③;其中,一定能判定的条件有 (填写所有正确的序号).
①③④
7.如图,MF⊥NF于点F,MF交AB于点E,NF交CD于
点G,∠1=140°,∠2=50°,试判断AB和CD的
位置关系,并说明理由.
Q
解:AB∥CD. 理由:
过点F向左作FQ,使∠MFQ=∠2=50°,
则∠NFQ=∠MFN-∠MFQ
=90°-50°=40°,
所以AB∥FQ.
又因为∠1=140°,
所以∠1+∠NFQ=180°,
所以CD∥FQ,所以AB∥CD.
课堂小结
名称 特征 基本图形 代表字母 相同点 共同特征
同位角
同旁 内角 内错角 F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:内部
截线:两侧
被截线:内部
1
2
1
2
1
2
都在截线同侧
都在被截线内部
这三类角都是没有公共顶点的
同位角、内错角、同旁内角
文字叙述 符号语言 图形
相等, 两直线平行 ∵ (已知), ∴a∥b
相等, 两直线平行 ∵ (已知), ∴a∥b 互补, 两直线平行 ∵ (已知) ∴a∥b 判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
第 二 章 相交线与平行线
2.2 探索直线平行的条件
第2课时 利用内错角、同旁内角
判定两条直线平行
学习目标
1.理解内错角、同旁内角的概念,结合图形识别内错角、同旁
内角;
2.会运用内错角、同旁内角判定两条直线平行.(重点、 难
点)
复习引入
我们已经学过的关于平行线内容有哪些?
平行于同一条直线的两条直线平行
经过直线外一点,有且只有一条直线与已知直线平行.
同位角相等,两直线平行.
思考:还有其他判定两条直线平行的方法吗?
知识讲解
一、内错角、同旁内角的概念
A
C
B
D
E
F
1
2
3
4
5
6
7
8
探究1 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB、CD内部
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
变形:图中的∠1与∠2都是内错角.
特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
A
C
B
D
E
F
1
2
3
4
5
6
7
8
探究2 观察∠4与∠5的位置关系:
①在直线EF的同旁
②在直线AB、CD内部
4
5
∠3和∠6
图中还有哪些同旁内角?
同旁内角
变形:图中的∠1与∠2都是同旁内角.
特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
如图,∠1与∠2是同旁内角吗?
名称 特征 基本图形 代表字母 相同点 共同特征
同位角
同旁 内角 内错角 F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:内部
截线:两侧
被截线:内部
1
2
1
2
1
2
都在截线同侧
都在被截线内部
这三类角都是没有公共顶点的
归纳总结
例1 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,
E
D
C
B
A
8
7
6
5
4
3
2
1
同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.
二、利用内错角、同旁内角判定两条直线平行
问题1:如图,由 3= 2,可推出a//b吗?如何推出的呢?
2
b
a
1
3
a//b(同位角相等,两直线平行).
解:
∵ 1= 3(已知),
3= 2(对顶角相等),
1= 2,
判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠3=∠2(已知),
∴a∥b(内错角相等,两直线平行).
应用格式:
2
b
a
1
3
问题2 : 如图,如果 1+ 2=180° ,你能判定a//b吗
c
2
b
a
1
3
解:能,
∵ 1+ 2=180°(已知),
1+ 3=180°(邻补角的性质),
2= 3(同角的补角相等),
a//b(同位角相等,两直线平行).
判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
3
∵∠1+∠2=180°(已知),
∴a∥b(同旁内角互补,两直线平行).
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
① ∵ ∠1 =_____(已知),
∴ AB∥CE( ).
② ∵ ∠1 +_____=180o(已知),
∴ CD∥BF( ).
③ ∵ ∠1 +∠5 =180o(已知),
∴ _____∥_____( ).
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知),
∴ CE∥AB( ).
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
例 根据条件完成填空.
当图中各角满足下列条件时,你能指出哪两条直线平行
(1) ∠1 = ∠4;
(2) ∠2 = ∠4;
(3) ∠1 + ∠3 =180 ;
a
b
l
m
n
1
2
3
4
.
.
练一练
2.如图,下列说法中不正确的是( )
A.∠1和∠3是同旁内角
B.∠2和∠3是内错角
C.∠2和∠4是同位角
D.∠3和∠5是对顶角
随堂训练
1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B B. ∠1=∠A
C. ∠3=∠B D. ∠3=∠A
C
1
2
3
A
E
B
C
D
C
3.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠4=180°,则a∥c
C
4.如图,已知∠1=30°,∠2或∠3满足条件
,则a//b.
2
1
3
a
b
c
∠2=150°或∠3=30°
5、一弯形轨道的拐角°,那么当另一拐角 时,.
D
C
B
A
60
6.如图,给出下列条件:①;②③;其中,一定能判定的条件有 (填写所有正确的序号).
①③④
7.如图,MF⊥NF于点F,MF交AB于点E,NF交CD于
点G,∠1=140°,∠2=50°,试判断AB和CD的
位置关系,并说明理由.
Q
解:AB∥CD. 理由:
过点F向左作FQ,使∠MFQ=∠2=50°,
则∠NFQ=∠MFN-∠MFQ
=90°-50°=40°,
所以AB∥FQ.
又因为∠1=140°,
所以∠1+∠NFQ=180°,
所以CD∥FQ,所以AB∥CD.
课堂小结
名称 特征 基本图形 代表字母 相同点 共同特征
同位角
同旁 内角 内错角 F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:内部
截线:两侧
被截线:内部
1
2
1
2
1
2
都在截线同侧
都在被截线内部
这三类角都是没有公共顶点的
同位角、内错角、同旁内角
文字叙述 符号语言 图形
相等, 两直线平行 ∵ (已知), ∴a∥b
相等, 两直线平行 ∵ (已知), ∴a∥b 互补, 两直线平行 ∵ (已知) ∴a∥b 判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
