2.1多边形(第1课时 多边形及多边形的内角和) 教学课件--湘教版数学八年级(下)
文档属性
| 名称 | 2.1多边形(第1课时 多边形及多边形的内角和) 教学课件--湘教版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:23:49 | ||
图片预览





文档简介
(共19张PPT)
第2章 四边形
2.1 多边形
第1课时 多边形及多边形的内角和
第2章 四边形
学 习 目 标
1.了解多边形及其有关概念;
2.探索并掌握多边形内角和定理,进一步了解转化的数学思想;(重点)
3.经历探索多边形的内角和公式的过程,会应用内角和公式解决问题.(难点)
新课导入
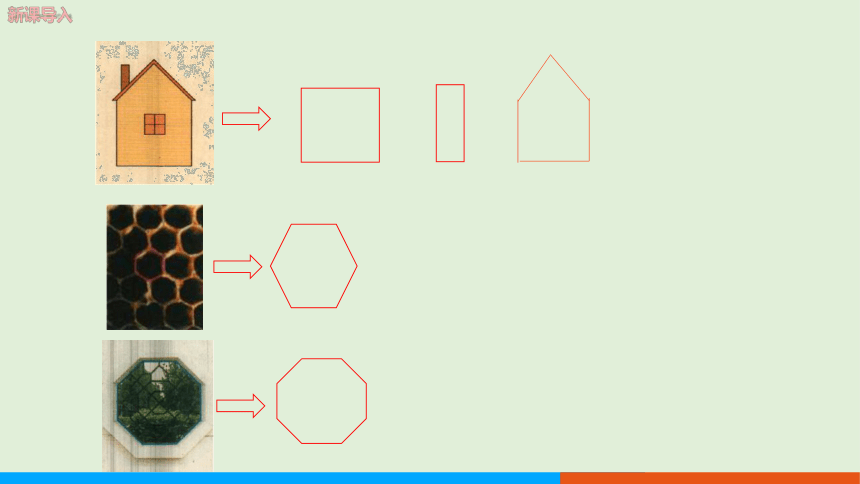
在实际生活当中,除了三角形,还有许多由线段围成的图形.观察图片,你能找到一些由线段围成的图形吗?
知识讲解
★ 多边形的定义
多边形的定义:
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
思考:比较多边形的定义与三角形的定义,为什么要强调“在平面内”呢?怎样命名多边形呢?
这是因为三角形中的三个顶点肯定都在同一个平面内,而四点,五点,甚至更多的点就有可能不在同一个平面内.
多边形用图形名称以及它的各个顶点的字母表示.字母要按照顶点的顺序书写,可以按顺时针或逆时针的顺序.
内角:多边形相邻两边组成的角
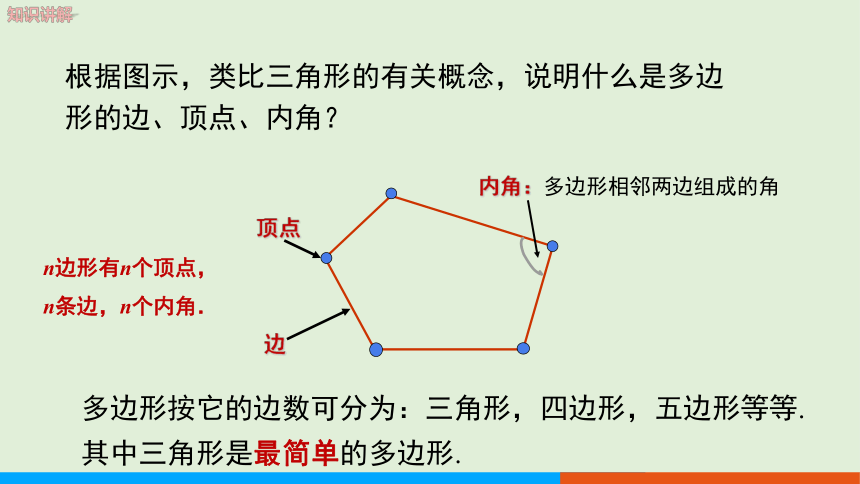
根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角?
顶点
边
n边形有n个顶点,n条边,n个内角.
多边形按它的边数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形.
★ 正多边形
定义:在平面内,边相等,角也都相等的多边形叫做正多边形.
正三角形
正方形
正五边形
正六边形
★多边形的对角线
A
B
C
D
E
定义:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
注意: 线段AC, AD是五边形ABCDE的一条对角线,多边形的对角线通常用虚线表示.
三角形
六边形
四边形
八边形
……
五边形
探究:请画出下列图形从某一顶点出发的对角线的条数:
多边形 三角形 四边形 五边形 六边形 八边形 n边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
0
1
2
3
5
n-3
1
2
3
4
6
n-2
小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
5×180°-360°
4×180°-180°
3×180°
六边形的内角和是多少呢?你能确定n边形的内角和吗?(n是大于或等于3的自然数)小组讨论后完成表格.
3×180°
多边形边数 图形 分成三角形的个数 内角和
3
4
5
6
7
… … … …
1
2
3
4
n-2
1×180°
2×180°
(n-2)×180°
4×180°
5×180°
n
5
n边形的内角和等于(n-2)·180°
多边形内角和定理:
正多边形内角的度数:
例1 如图,四边形中,∠A+∠C=180°,∠B与∠D有怎样的关系?
例题讲解
解:∠B+∠D=180°
例2 一个多边形的内角和为1440°,则它是几边形?
解:设这个多边形是n边形,则
180°·(n-2)=1440°,
解得 n=10,
所以 这个多边形是10边形.
1.六边形的内角和为( )
A.1260° B.1080° C.900° D.720°
2.下列角度中能成为某多边形的内角和的是( )
A.270° B.560° C.1 800° D.1 900°
3.八边形的七个内角都为150°,则第八个内角等于________
C
D
30°
随堂训练
4.正八边形的每个内角都是( )
A.60° B.80° C.100° D.135°
5.一个多边形的每个内角均为120°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
D
C
6.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形是几边形?它的内角和是多少?
七边形,内角和为900°
1.多边形的内角和定理:
n边形的内角和等于(n-2)·180°
2、正多边形内角的度数:
课堂小结
第2章 四边形
2.1 多边形
第1课时 多边形及多边形的内角和
第2章 四边形
学 习 目 标
1.了解多边形及其有关概念;
2.探索并掌握多边形内角和定理,进一步了解转化的数学思想;(重点)
3.经历探索多边形的内角和公式的过程,会应用内角和公式解决问题.(难点)
新课导入
在实际生活当中,除了三角形,还有许多由线段围成的图形.观察图片,你能找到一些由线段围成的图形吗?
知识讲解
★ 多边形的定义
多边形的定义:
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
思考:比较多边形的定义与三角形的定义,为什么要强调“在平面内”呢?怎样命名多边形呢?
这是因为三角形中的三个顶点肯定都在同一个平面内,而四点,五点,甚至更多的点就有可能不在同一个平面内.
多边形用图形名称以及它的各个顶点的字母表示.字母要按照顶点的顺序书写,可以按顺时针或逆时针的顺序.
内角:多边形相邻两边组成的角
根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角?
顶点
边
n边形有n个顶点,n条边,n个内角.
多边形按它的边数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形.
★ 正多边形
定义:在平面内,边相等,角也都相等的多边形叫做正多边形.
正三角形
正方形
正五边形
正六边形
★多边形的对角线
A
B
C
D
E
定义:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
注意: 线段AC, AD是五边形ABCDE的一条对角线,多边形的对角线通常用虚线表示.
三角形
六边形
四边形
八边形
……
五边形
探究:请画出下列图形从某一顶点出发的对角线的条数:
多边形 三角形 四边形 五边形 六边形 八边形 n边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
0
1
2
3
5
n-3
1
2
3
4
6
n-2
小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
5×180°-360°
4×180°-180°
3×180°
六边形的内角和是多少呢?你能确定n边形的内角和吗?(n是大于或等于3的自然数)小组讨论后完成表格.
3×180°
多边形边数 图形 分成三角形的个数 内角和
3
4
5
6
7
… … … …
1
2
3
4
n-2
1×180°
2×180°
(n-2)×180°
4×180°
5×180°
n
5
n边形的内角和等于(n-2)·180°
多边形内角和定理:
正多边形内角的度数:
例1 如图,四边形中,∠A+∠C=180°,∠B与∠D有怎样的关系?
例题讲解
解:∠B+∠D=180°
例2 一个多边形的内角和为1440°,则它是几边形?
解:设这个多边形是n边形,则
180°·(n-2)=1440°,
解得 n=10,
所以 这个多边形是10边形.
1.六边形的内角和为( )
A.1260° B.1080° C.900° D.720°
2.下列角度中能成为某多边形的内角和的是( )
A.270° B.560° C.1 800° D.1 900°
3.八边形的七个内角都为150°,则第八个内角等于________
C
D
30°
随堂训练
4.正八边形的每个内角都是( )
A.60° B.80° C.100° D.135°
5.一个多边形的每个内角均为120°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
D
C
6.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形是几边形?它的内角和是多少?
七边形,内角和为900°
1.多边形的内角和定理:
n边形的内角和等于(n-2)·180°
2、正多边形内角的度数:
课堂小结
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
