2.2.1平行四边形的性质(第2课时平行四边形对角线的性质) 教学课件--湘教版数学八年级(下)
文档属性
| 名称 | 2.2.1平行四边形的性质(第2课时平行四边形对角线的性质) 教学课件--湘教版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第2章 四边形
2.2.1 平行四边形的性质
第2课时 平行四边形对角线的性质
第2章 四边形
学 习 目 标
1.掌握平行四边形对角线互相平分的性质.(重点)
2.综合运用平行四边形的性质,并能够利用性质进行简单的推理计算.(难点)
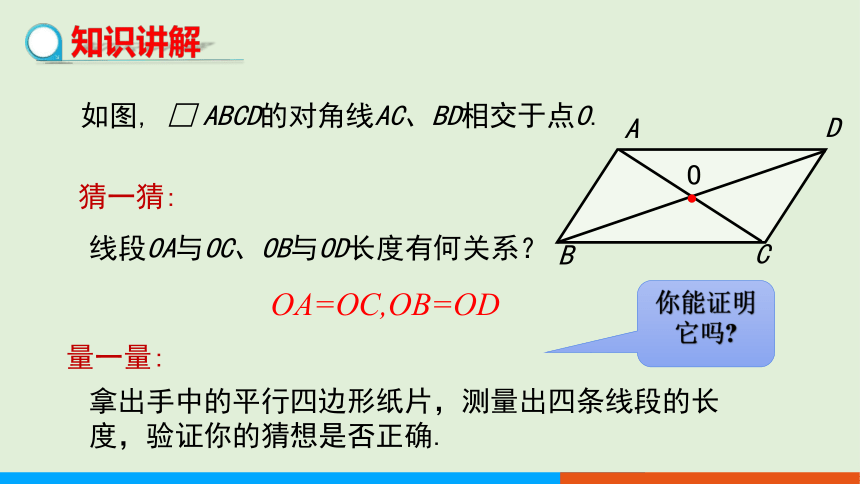
如图, □ ABCD的对角线AC、BD相交于点O.
A
C
D
B
●
O
猜一猜:
线段OA与OC、OB与OD长度有何关系?
量一量:
拿出手中的平行四边形纸片,测量出四条线段的长度,验证你的猜想是否正确.
知识讲解
OA=OC,OB=OD
你能证明 它吗
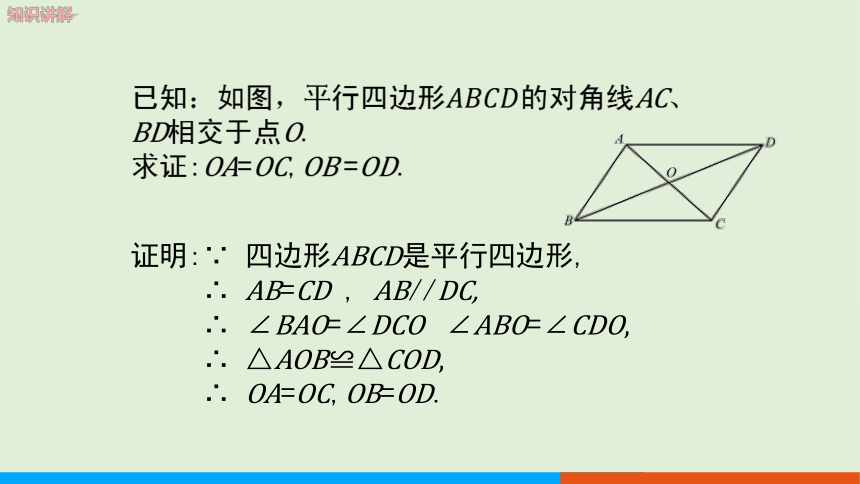
已知:如图,平行四边形的对角线AC、
BD相交于点O.
求证:OA=OC,OB =OD.
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD , AB//DC,
∴ ∠BAO=∠DCO ∠ABO=∠CDO,
∴ △AOB≌△COD,
∴ OA=OC,OB=OD.
平行四边形的对角线互相平分.
平行四边形的性质
应用格式:
∵四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
总 结
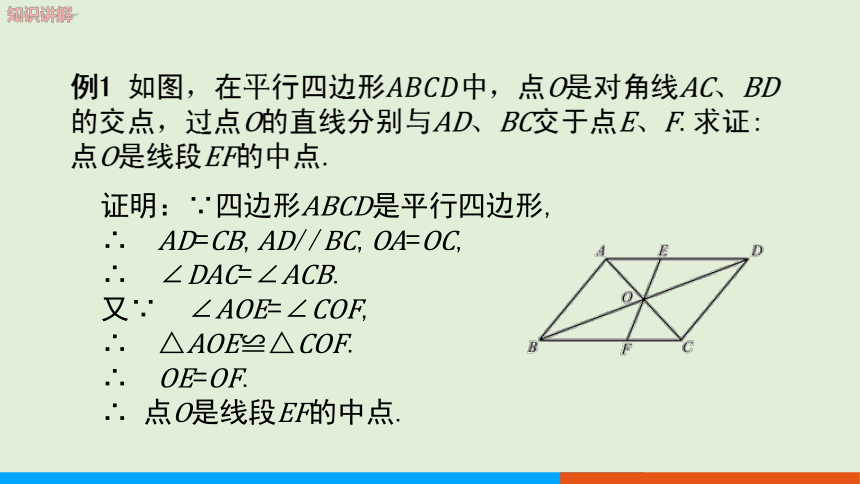
例1 如图,在平行四边形中,点O是对角线AC、BD的交点,过点O的直线分别与AD、BC交于点E、F.求证:点O是线段EF的中点.
证明:∵四边形ABCD是平行四边形,
∴ AD=CB,AD//BC,OA=OC,
∴ ∠DAC=∠ACB.
又∵ ∠AOE=∠COF,
∴ △AOE≌△COF.
∴ OE=OF.
∴ 点O是线段EF的中点.
例2 已知 ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,求这个平行四边形各边的长.
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5cm,
∴AB-AD=5cm.
又∵ ABCD的周长为60cm,∴AB+AD=30cm,
则AB=CD=17.5cm,AD=BC=12.5cm.
规律总结:平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于四边形邻边边长之差.
拓展延伸
平行四边形的面积
例3 如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.
解:设AB=x,则BC=24-x.
根据平行四边形的面积公式可得5x=10(24-x),
解得x=16.
则平行四边形ABCD的面积为5×16=80.
规律总结
已知平行四边形的高DE,DF,根据“等面积法”及平行四边形的性质列方程求解.
思考 平行四边形的对角线分平行四边形ABCD为四个三角形,它们的面积有怎样的关系呢?
解:相等.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵△ADO与△ODC等底同高,
∴S△ADO=S△ODC.
同理可得S△ADO=S△ODC=S△BCO=S△AOB.
还可结合全等来证哟.
规律总结
平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
随堂训练
1.如图, □ABCD的对角线AC、BD相交于点O,且 AC+BD=16,CD=6,则△ABO的周长是( )
A. 10 B. 14 C. 20 D. 22
B
B
C
D
A
O
2.如图, □ ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A.16 B.14 C.12 D.10
A
D
C
B
F
E
O
C
3.如图,在□ ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 _____________
O
B
A
C
●
1<<9
4.如图,平行四边形ABCD的面积为20,对角线AC,BD相交于点O,点E,F分别是AB,CD上的点,且AE=DF,则图中阴影部分的面积为_______.
5
5.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长是多少?
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD.
∵OE⊥BD,
∴BE=DE.
∵△CDE的周长为10,
∴DE+CE+CD=BE+CE+CD=BC+CD=10,
∴平行四边形ABCD的周长为
2×(BC+CD)=20.
第2章 四边形
2.2.1 平行四边形的性质
第2课时 平行四边形对角线的性质
第2章 四边形
学 习 目 标
1.掌握平行四边形对角线互相平分的性质.(重点)
2.综合运用平行四边形的性质,并能够利用性质进行简单的推理计算.(难点)
如图, □ ABCD的对角线AC、BD相交于点O.
A
C
D
B
●
O
猜一猜:
线段OA与OC、OB与OD长度有何关系?
量一量:
拿出手中的平行四边形纸片,测量出四条线段的长度,验证你的猜想是否正确.
知识讲解
OA=OC,OB=OD
你能证明 它吗
已知:如图,平行四边形的对角线AC、
BD相交于点O.
求证:OA=OC,OB =OD.
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD , AB//DC,
∴ ∠BAO=∠DCO ∠ABO=∠CDO,
∴ △AOB≌△COD,
∴ OA=OC,OB=OD.
平行四边形的对角线互相平分.
平行四边形的性质
应用格式:
∵四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
总 结
例1 如图,在平行四边形中,点O是对角线AC、BD的交点,过点O的直线分别与AD、BC交于点E、F.求证:点O是线段EF的中点.
证明:∵四边形ABCD是平行四边形,
∴ AD=CB,AD//BC,OA=OC,
∴ ∠DAC=∠ACB.
又∵ ∠AOE=∠COF,
∴ △AOE≌△COF.
∴ OE=OF.
∴ 点O是线段EF的中点.
例2 已知 ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,求这个平行四边形各边的长.
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5cm,
∴AB-AD=5cm.
又∵ ABCD的周长为60cm,∴AB+AD=30cm,
则AB=CD=17.5cm,AD=BC=12.5cm.
规律总结:平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于四边形邻边边长之差.
拓展延伸
平行四边形的面积
例3 如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.
解:设AB=x,则BC=24-x.
根据平行四边形的面积公式可得5x=10(24-x),
解得x=16.
则平行四边形ABCD的面积为5×16=80.
规律总结
已知平行四边形的高DE,DF,根据“等面积法”及平行四边形的性质列方程求解.
思考 平行四边形的对角线分平行四边形ABCD为四个三角形,它们的面积有怎样的关系呢?
解:相等.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵△ADO与△ODC等底同高,
∴S△ADO=S△ODC.
同理可得S△ADO=S△ODC=S△BCO=S△AOB.
还可结合全等来证哟.
规律总结
平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
随堂训练
1.如图, □ABCD的对角线AC、BD相交于点O,且 AC+BD=16,CD=6,则△ABO的周长是( )
A. 10 B. 14 C. 20 D. 22
B
B
C
D
A
O
2.如图, □ ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A.16 B.14 C.12 D.10
A
D
C
B
F
E
O
C
3.如图,在□ ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 _____________
O
B
A
C
●
1<<9
4.如图,平行四边形ABCD的面积为20,对角线AC,BD相交于点O,点E,F分别是AB,CD上的点,且AE=DF,则图中阴影部分的面积为_______.
5
5.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长是多少?
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD.
∵OE⊥BD,
∴BE=DE.
∵△CDE的周长为10,
∴DE+CE+CD=BE+CE+CD=BC+CD=10,
∴平行四边形ABCD的周长为
2×(BC+CD)=20.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
